Wrap-up and remarks

Credit Risk Modeling in R

Lore Dirick

Manager of Data Science Curriculum at Flatiron School

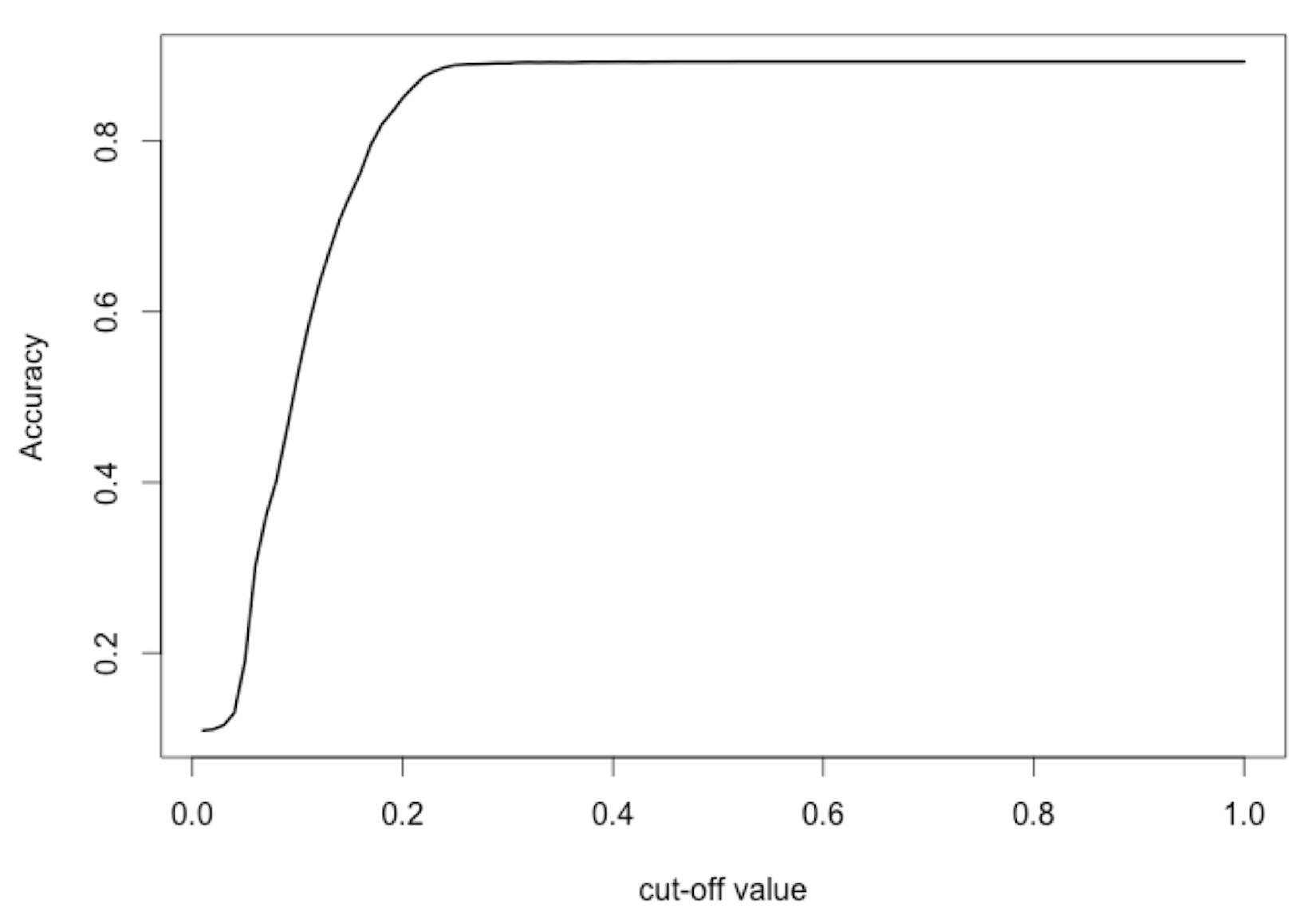
Best cut-off for accuracy?

Screen Shot 2020-06-22 at 2.42.06 PM.png

$\text{Accuracy} = \frac{TP + TN}{TP + FP + TN + FN}$

Best cut-off for accuracy?

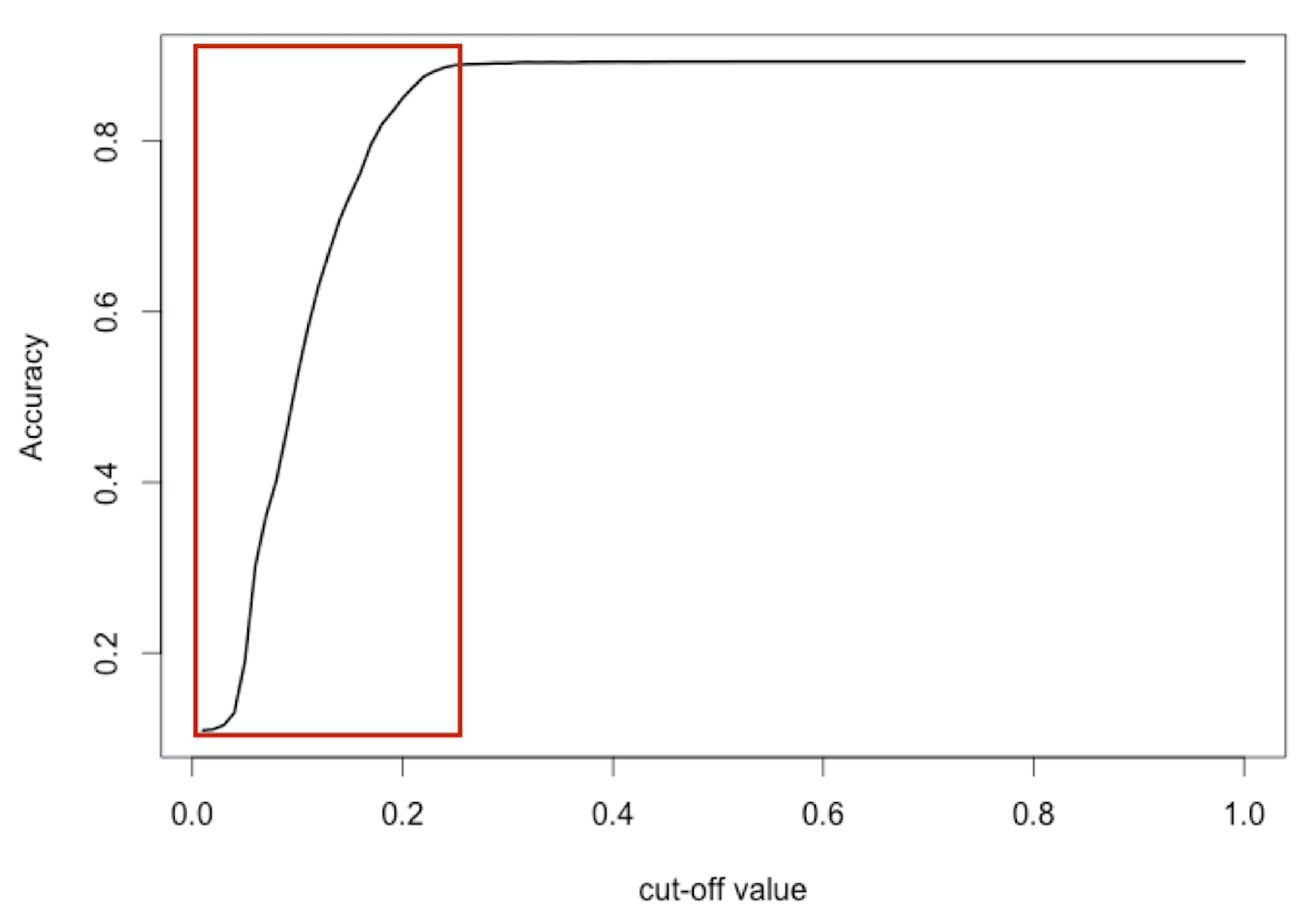
Screen Shot 2020-06-22 at 2.42.20 PM.png

$\text{Accuracy} = \frac{TP + TN}{TP + FP + TN + FN}$

Best cut-off for accuracy?

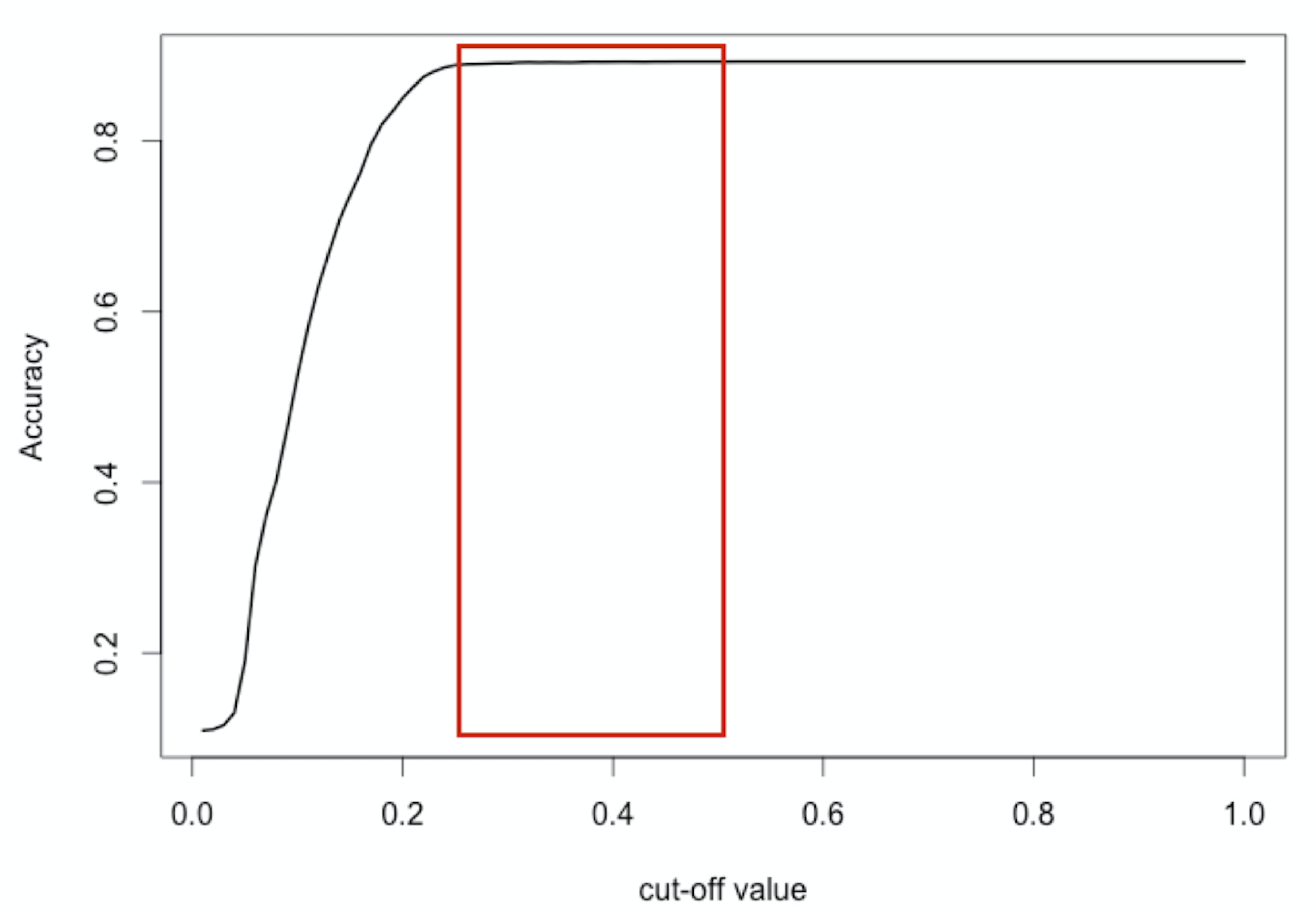
Screen Shot 2020-06-22 at 2.42.36 PM.png

$\text{Accuracy} = \frac{TP + TN}{TP + FP + TN + FN}$

Best cut-off for accuracy?

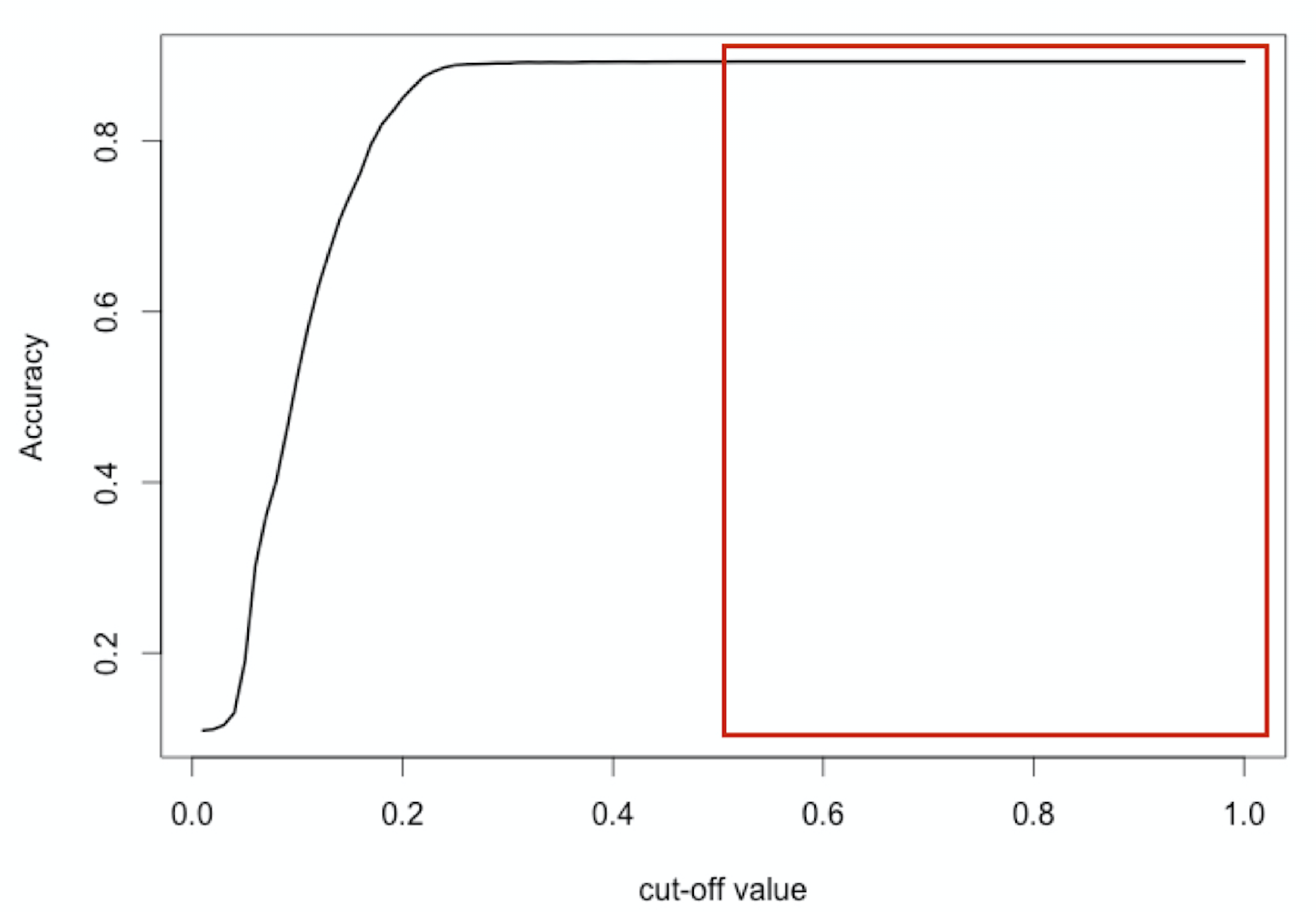
Screen Shot 2020-06-22 at 2.42.50 PM.png

$\text{Accuracy} = \frac{TP + TN}{TP + FP + TN + FN}$

Best cut-off for accuracy?

Screen Shot 2020-06-22 at 2.42.50 PM.png

$\text{Accuracy} = 89.31\%$

$\text{Actual defaults in test set} = 10.69\%$

$$ = (100 - 89.31)\%$$

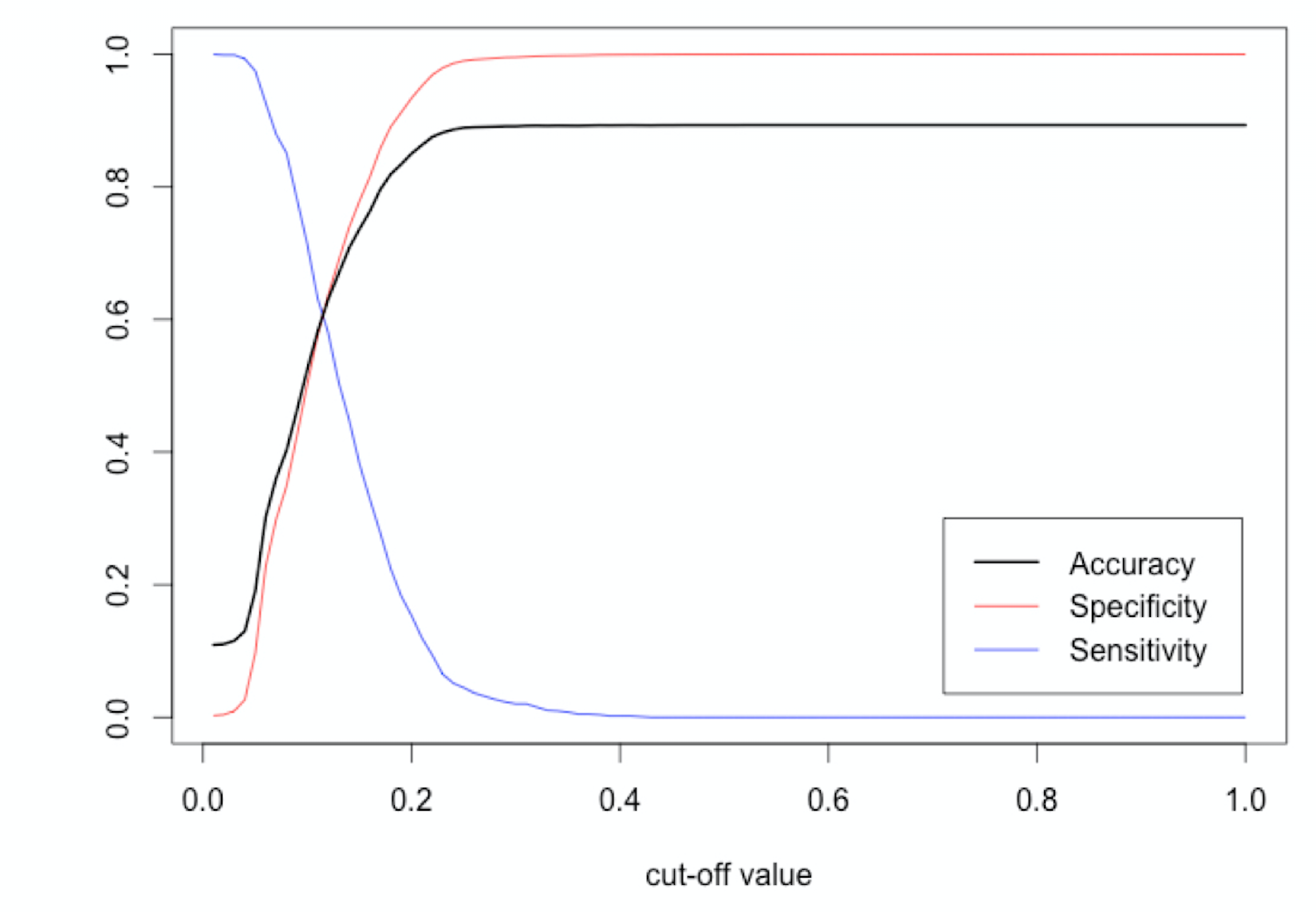
What about sensitivity or specificity?

Screen Shot 2020-06-22 at 2.43.10 PM.png

$\text{Sensitivity} = 1037 / (1037 + 0) = 100\%$

$\text{Specificity} = 0 / (0 + 864) = 0\%$

What about sensitivity or specificity?

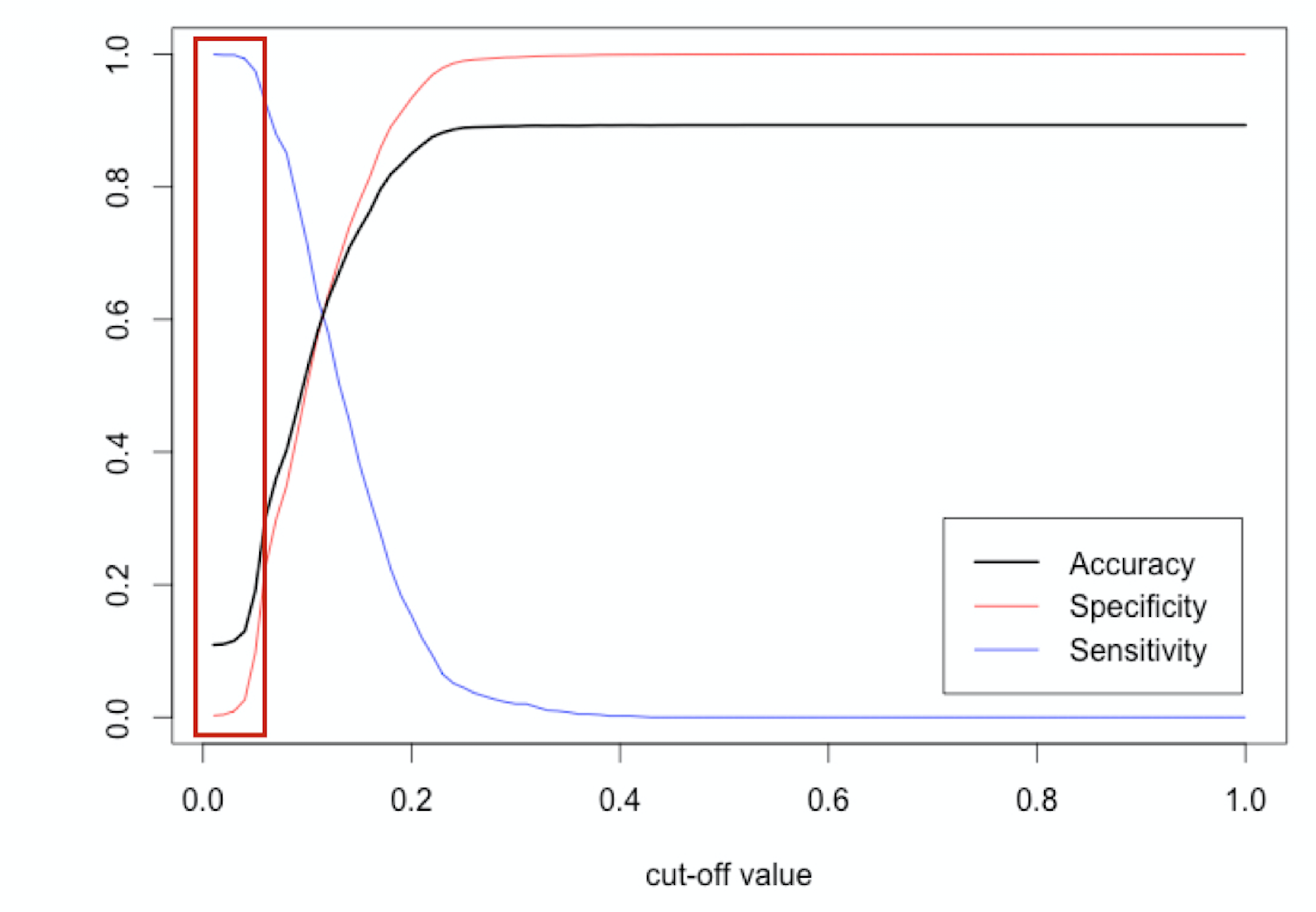
Screen Shot 2020-06-22 at 2.43.24 PM.png

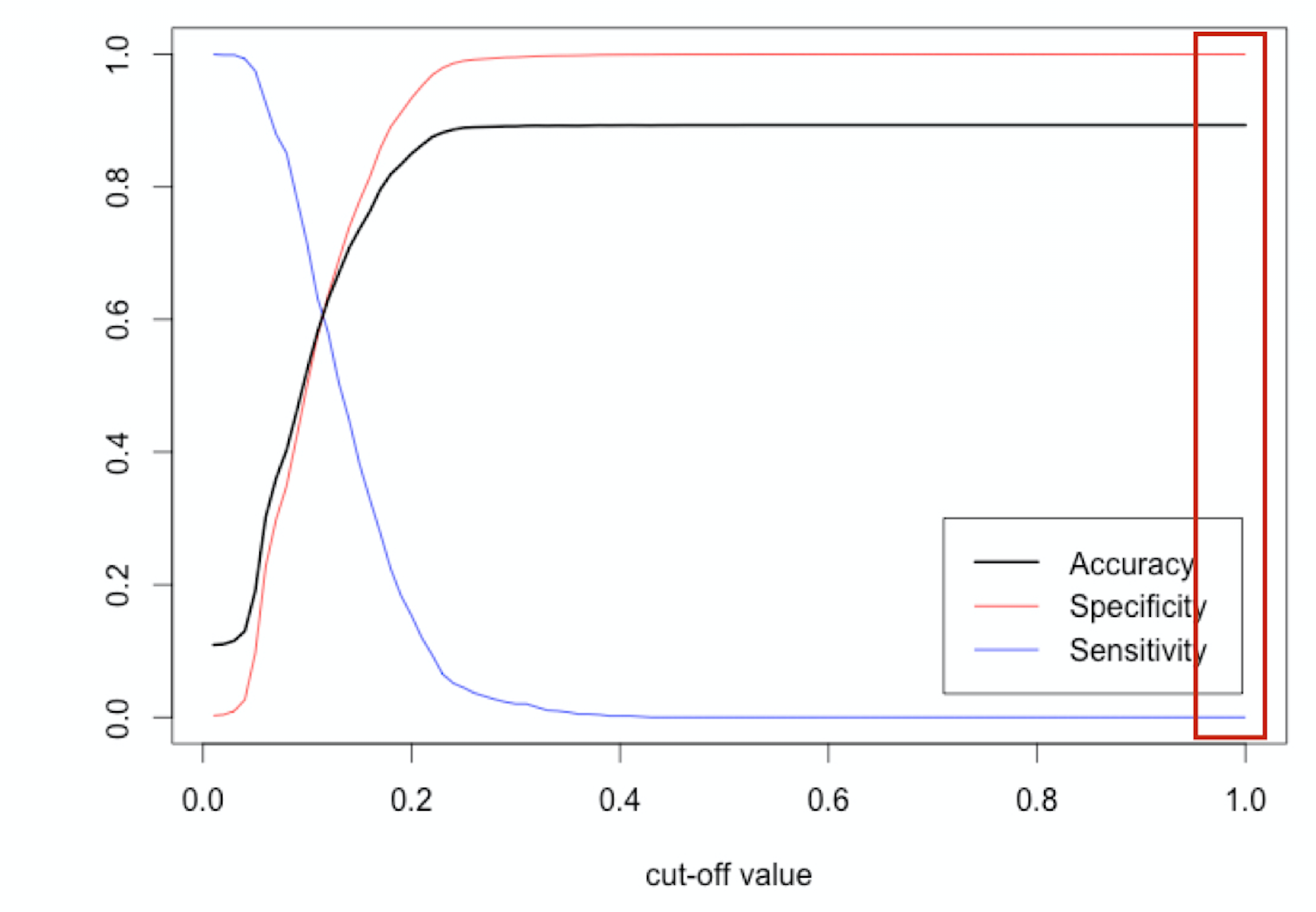
What about sensitivity or specificity?

Screen Shot 2020-06-22 at 2.43.39 PM.png

$\text{Sensitivity} = 0 / (0 + 1037) = 0\%$

$\text{Specificity} = 8640 / (8640 + 0) = 100\%$

About logistic regression…

log_model_full <- glm(loan_status ~ ., family = "binomial", data = training_set)

Is the same as:

log_model_full <- glm(loan_status ~ ., family = binomial(link = logit), data = training_set)

Recall:

$$P({\text{loan status}}=1|x_1,...,x_m) = \frac{1}{1+e^{-(\beta_0 + \beta_1 x_1 + ... + \beta_m x_m)}}$$

log_model_full <- glm(loan_status ~ ., 
                      family = binomial(link = probit), 
                      data = training_set)

log_model_full <- glm(loan_status ~ ., 
                      family = binomial(link = cloglog), 
                      data = training_set)

$\beta_j < 0$
- The probability of default decreases as $x_j$ increases
$\beta_j > 0$
- The probability of default increases as $x_j$ increases

$$P({\text{loan status}}=1|x_1,...,x_m) = \frac{1}{1+e^{-(\beta_0 + \beta_1 x_1 + ... + \beta_m x_m)}}$$

Let's practice!

Credit Risk Modeling in R