The ROC-curve
Credit Risk Modeling in R

Lore Dirick
Manager of Data Science Curriculum at Flatiron School
Until now
- Strategy table/curve : still make assumption
- What is "overall" best model?
Confusion matrix
$$
Actual loan status v. Model prediction
| No default (0) | Default (1) | |
|---|---|---|
| No default (0) | TN | FP |
| Default (1) | FN | TP |
$$
$\text{Accuracy} = \frac{TP +TN}{TP + FP + TN + FN}$
$\text{Sensitivity} = \frac{TP}{TP + FN}$
$\text{Specificity} = \frac{TN}{TN + FP}$
Accuracy?
$$
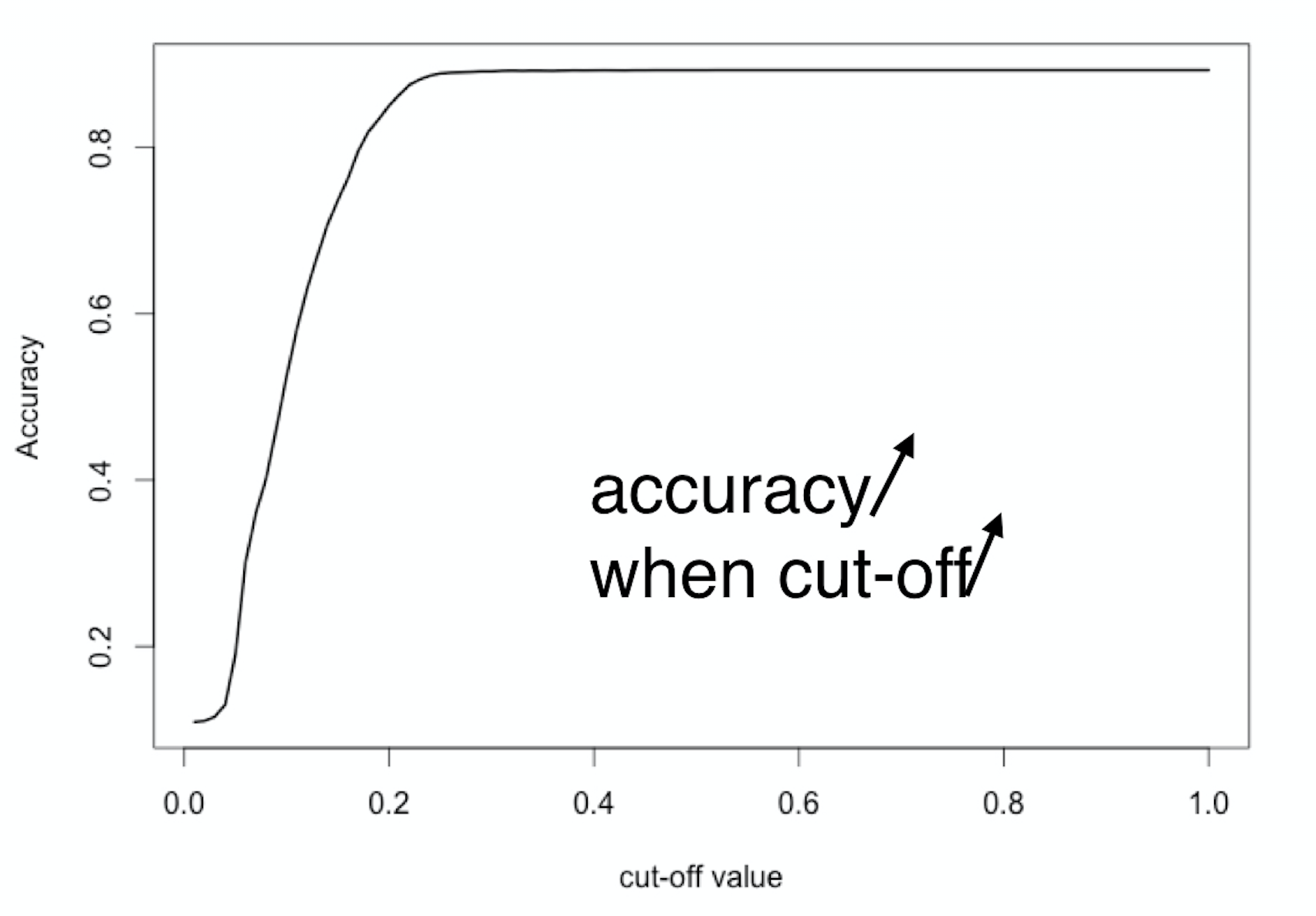
$$
$\text{Sensitivity} = \frac{TP}{TP + FN}$
$\text{Specificity} = \frac{TN}{TN + FP}$
The ROC-curve
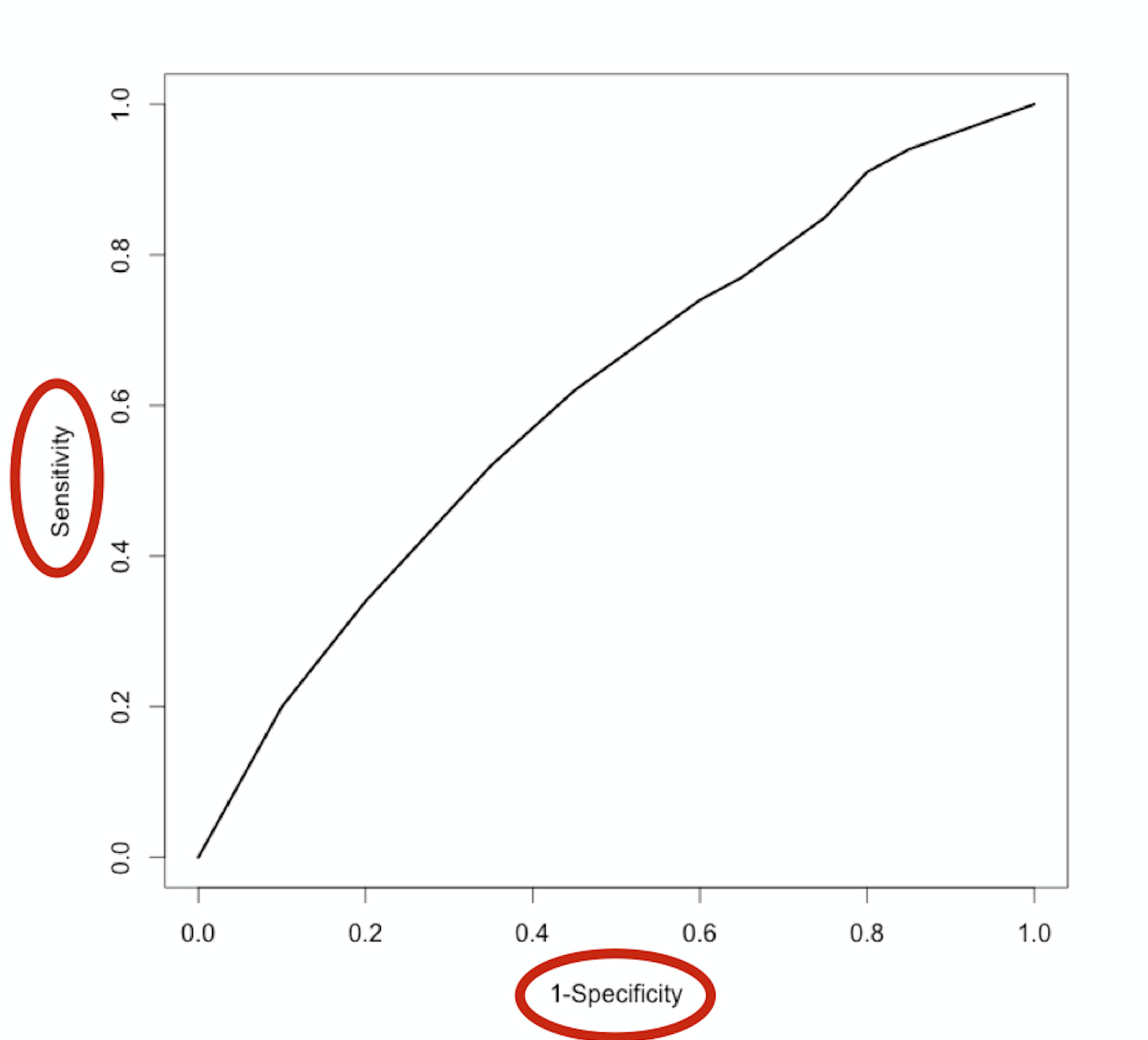
$$
$\text{Sensitivity} = \frac{TP}{TP + FN}$
$\text{Specificity} = \frac{TN}{TN + FP}$
The ROC-curve
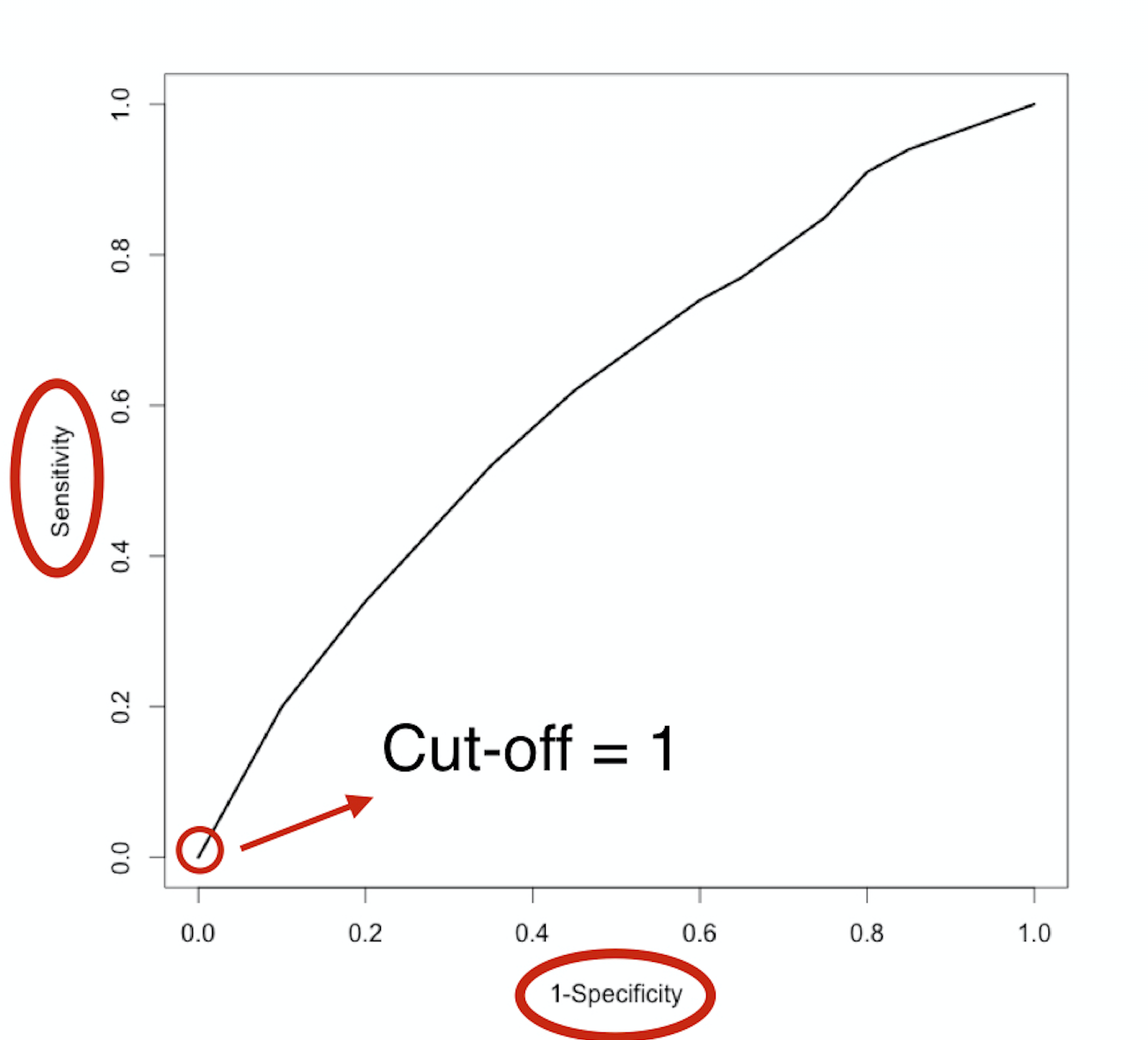
$$
$\text{Sensitivity} = \frac{TP}{TP + FN}$
$\text{Specificity} = \frac{TN}{TN + FP}$
The ROC-curve
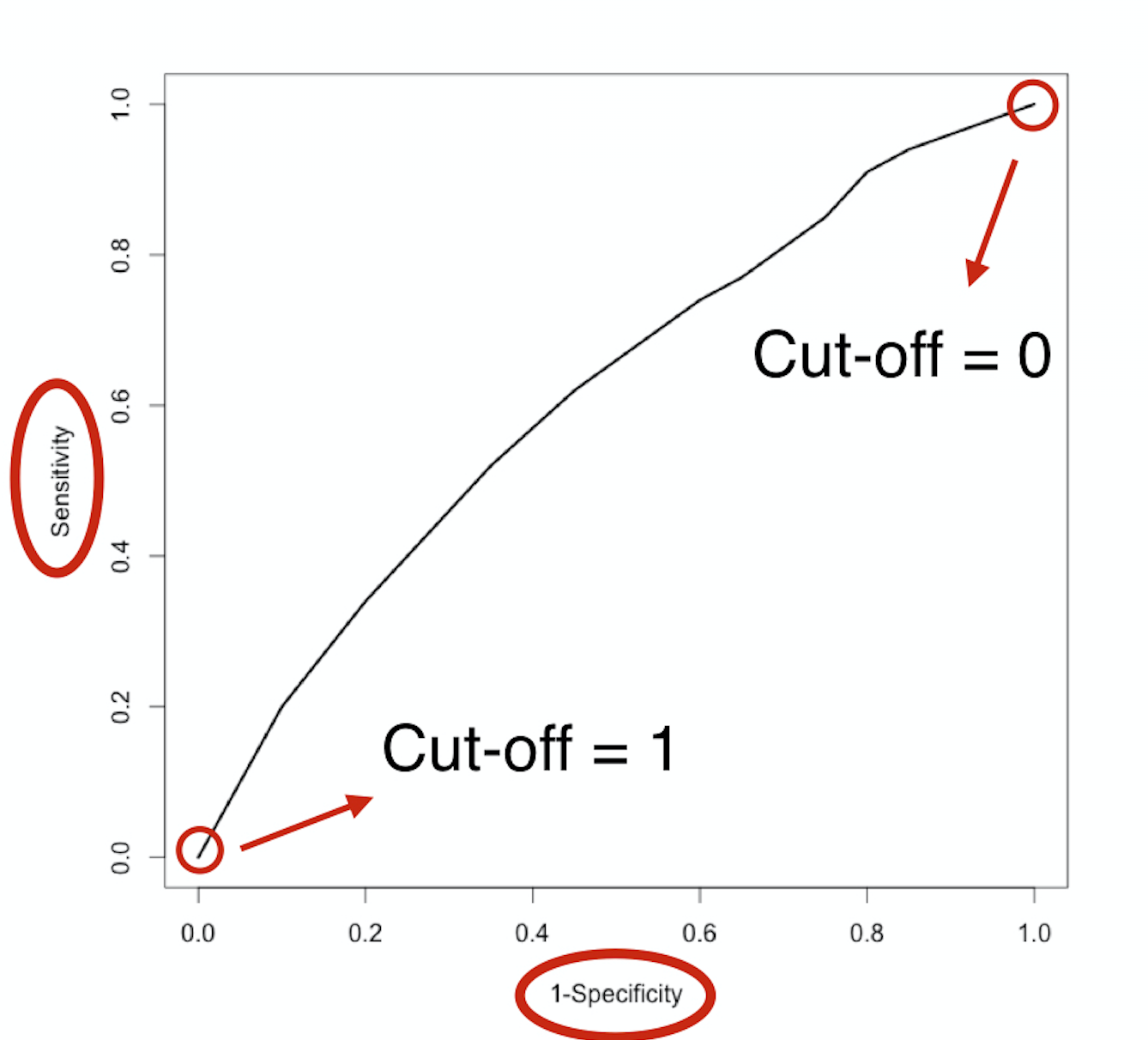
$$
$\text{Sensitivity} = \frac{TP}{TP + FN}$
$\text{Specificity} = \frac{TN}{TN + FP}$
The ROC-curve
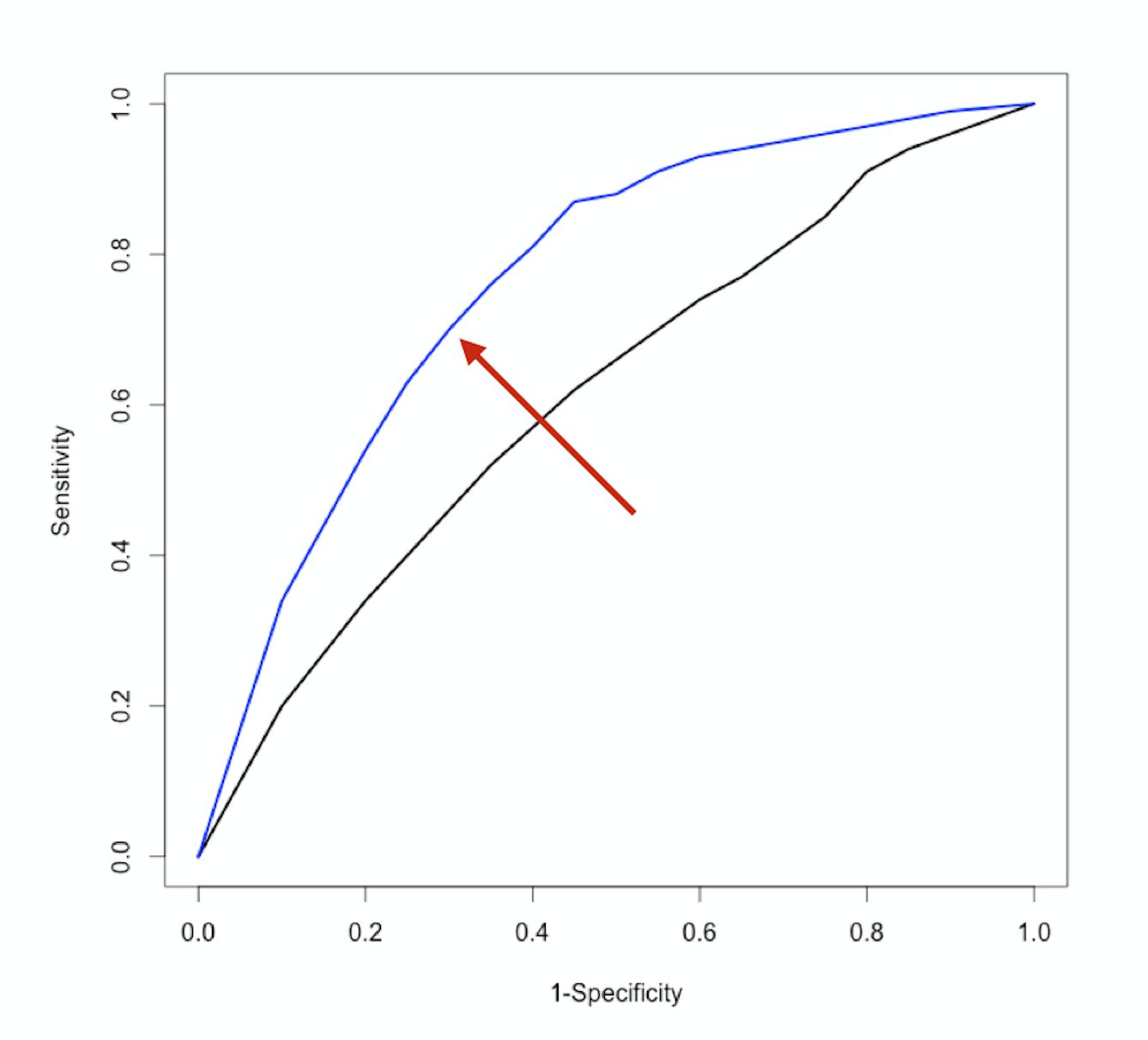
$$
$\text{Sensitivity} = \frac{TP}{TP + FN}$
$\text{Specificity} = \frac{TN}{TN + FP}$
The ROC-curve
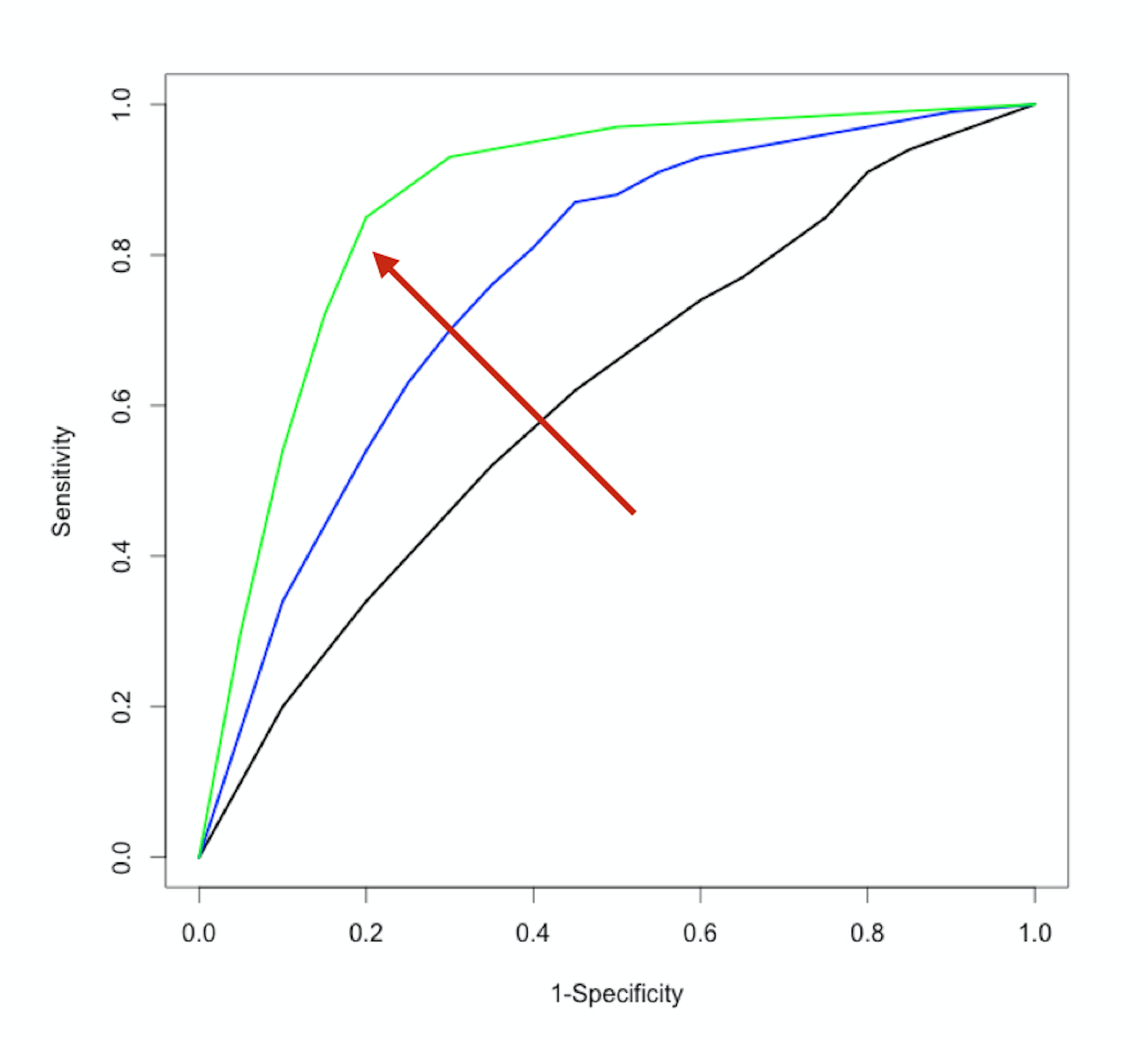
$$
$\text{Sensitivity} = \frac{TP}{TP + FN}$
$\text{Specificity} = \frac{TN}{TN + FP}$
The ROC-curve
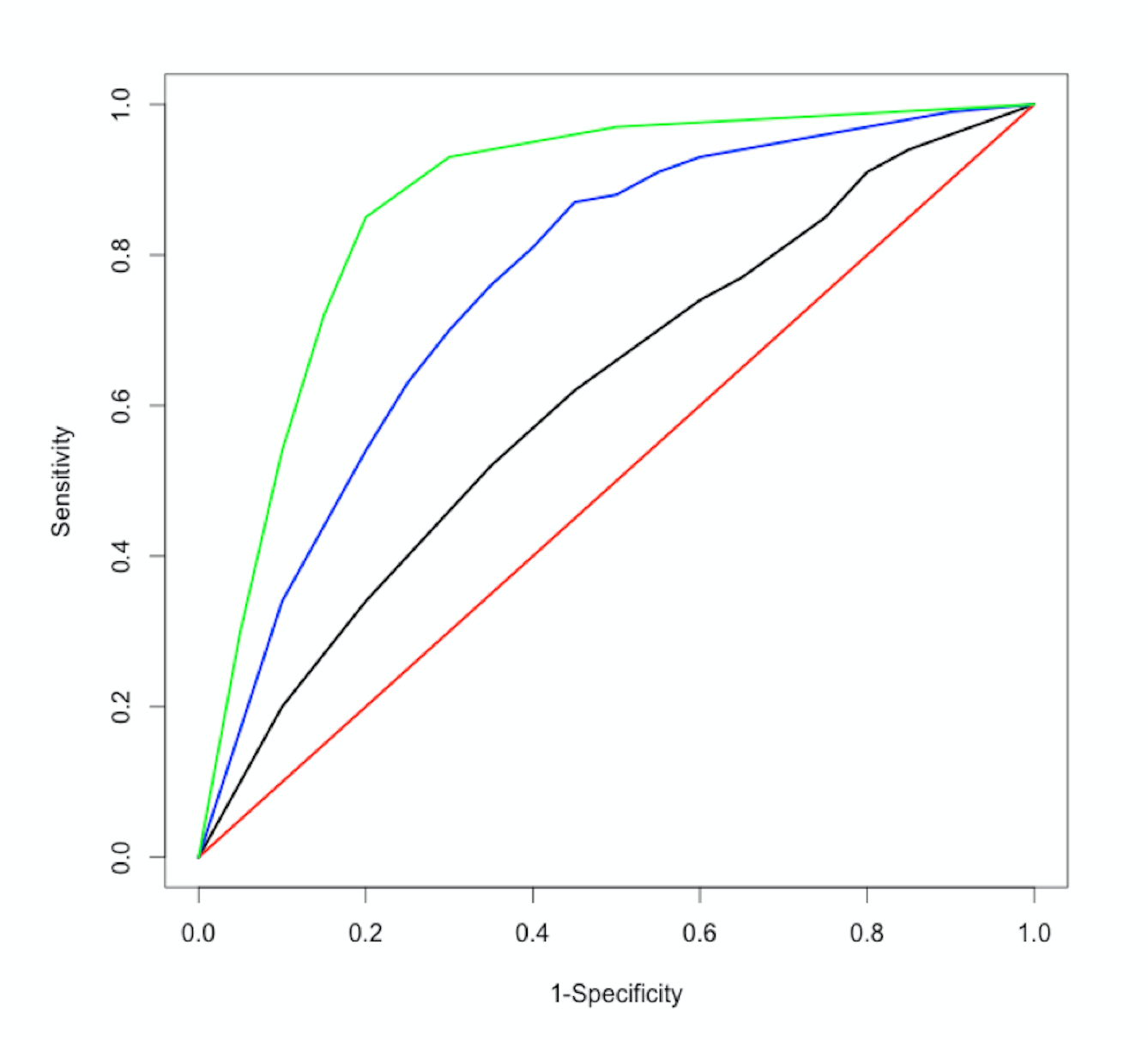
$$
$\text{Sensitivity} = \frac{TP}{TP + FN}$
$\text{Specificity} = \frac{TN}{TN + FP}$
Which one is better?
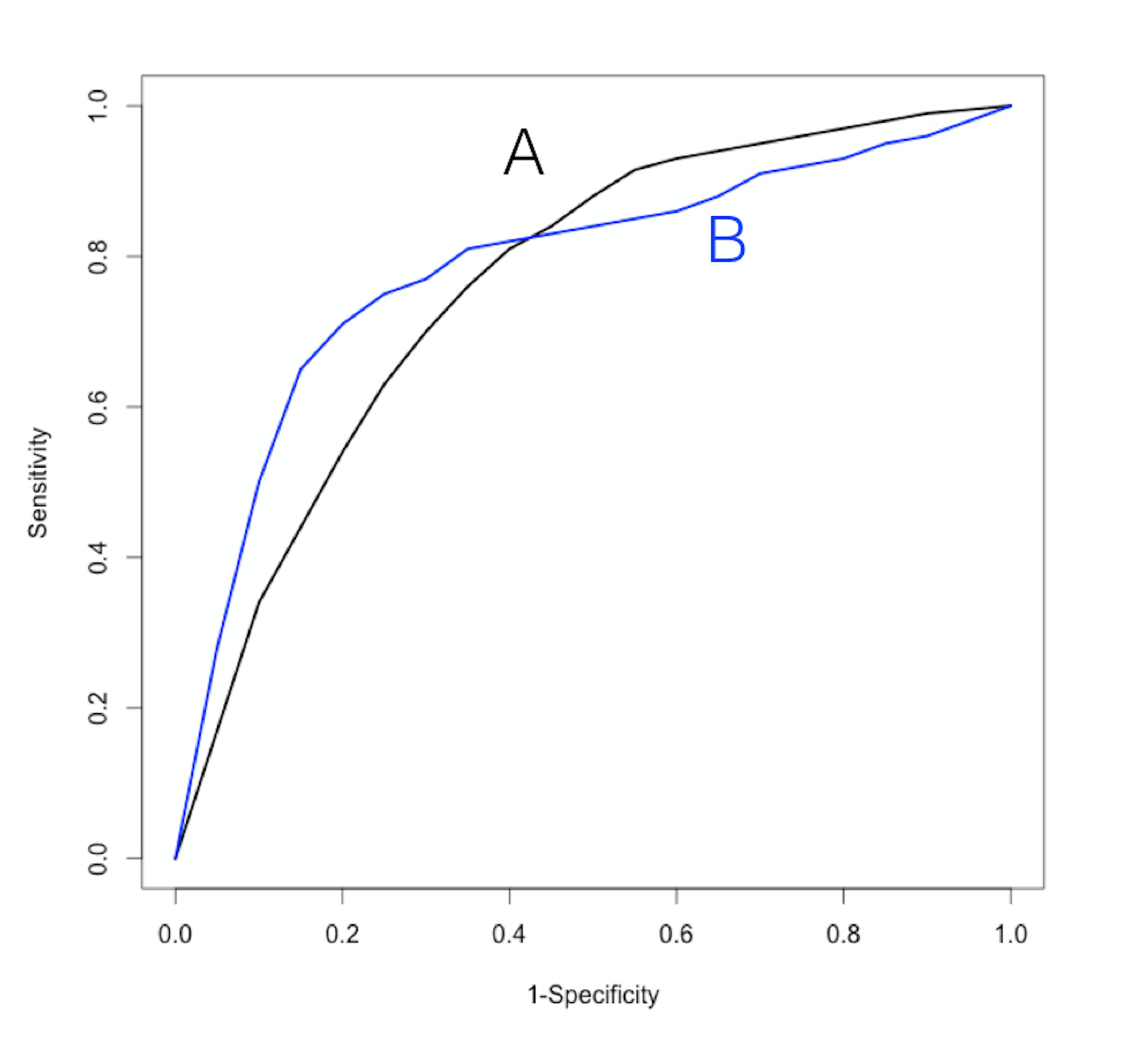
- AUC ROC-curve
A = 0.75 - AUC ROC-curve
B = 0.78
Let's practice!
Credit Risk Modeling in R

