The autoregressive model
Time Series Analysis in R

David S. Matteson
Associate Professor at Cornell University
The autoregressive model - I
The Autoregressive (AR) recursion:
$Today = Constant + Slope * Yesterday + Noise $
Mean centered version:
$(Today - Mean) = $
$ Slope*(Yesterday - Mean) + Noise $
The autoregressive model - II
$$(Today - Mean) = $$
$$Slope * (Yesterday - Mean) + Noise$$
More formally: $$ Y_t - \mu = \phi (Y_{t-1} - \mu ) + \epsilon_t$$ where $ \epsilon_t$ is mean zero white noise (WN).
- The mean $ \mu$
- The slope $ \phi$
- The WN variance $ \sigma ^2$
AR processes - I
$$Y_t - \mu = \phi(Y_{t-1} - \mu) + \epsilon_t$$
- If slope $ \phi = 0 $ then: $Y_t = \mu + \epsilon_t $ and
And $Y_t$ is white noise: $(\mu, \sigma _{\epsilon}^2)$
- If slope $ \phi \neq 0 $ then: $ Y_t$ depends on both $ \epsilon_t$ and $ Y_{t-1} $
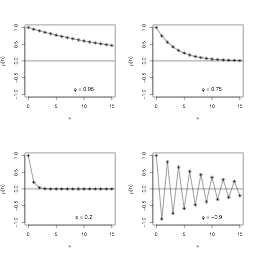
And the process {${Y_t}$} is autocorrelated
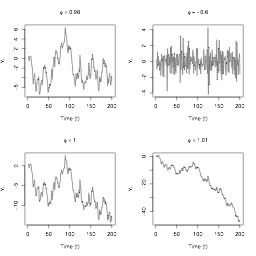
Large values of $ \phi$ lead to greater autocorrelation
Negative values of $ \phi$ result in oscillatory time series
AR examples
Autocorrelations
Random walk
If $ \mu = 0$ and slope $ \phi = 1$, then:
$$Y_t = Y_{t-1} + \epsilon_t$$
Which is:
$Today = Yesterday + Noise $
But this is a random walk.
And {$ Y_t $} is not stationary in this case.
Let's practice!
Time Series Analysis in R

