Compare AR and MA models
Time Series Analysis in R

David S. Matteson
Associate Professor at Cornell University
MA and AR processes
MA model: $Today = Mean + Noise + Slope * (Yesterday's Noise)$ $$Y_t = \mu + \epsilon_t + \theta\epsilon_{t-1}$$
AR model:
$(Today - Mean) = Slope*(Yesterday - Mean)$ $$+ Noise$$ $$Y_t - \mu = \phi(Y_{t-1} - \mu) +\epsilon_t$$
- Where:
$$\epsilon_t \sim WhiteNoise(0, \sigma^2_t)$$
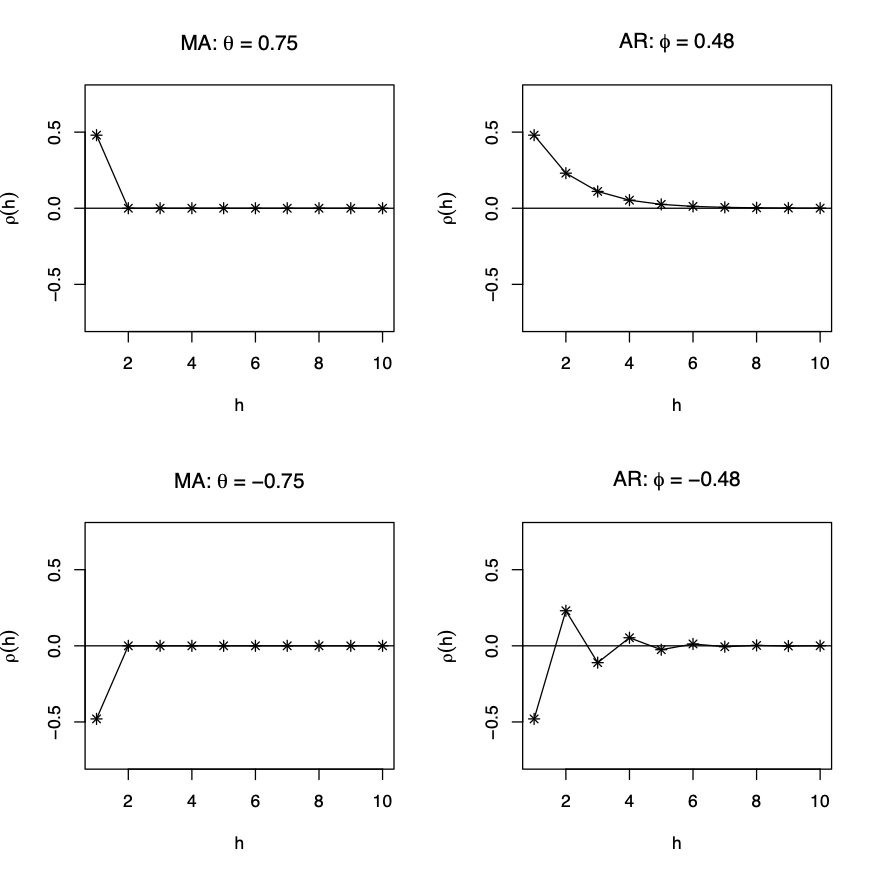
MA and AR processes: autocorrelations
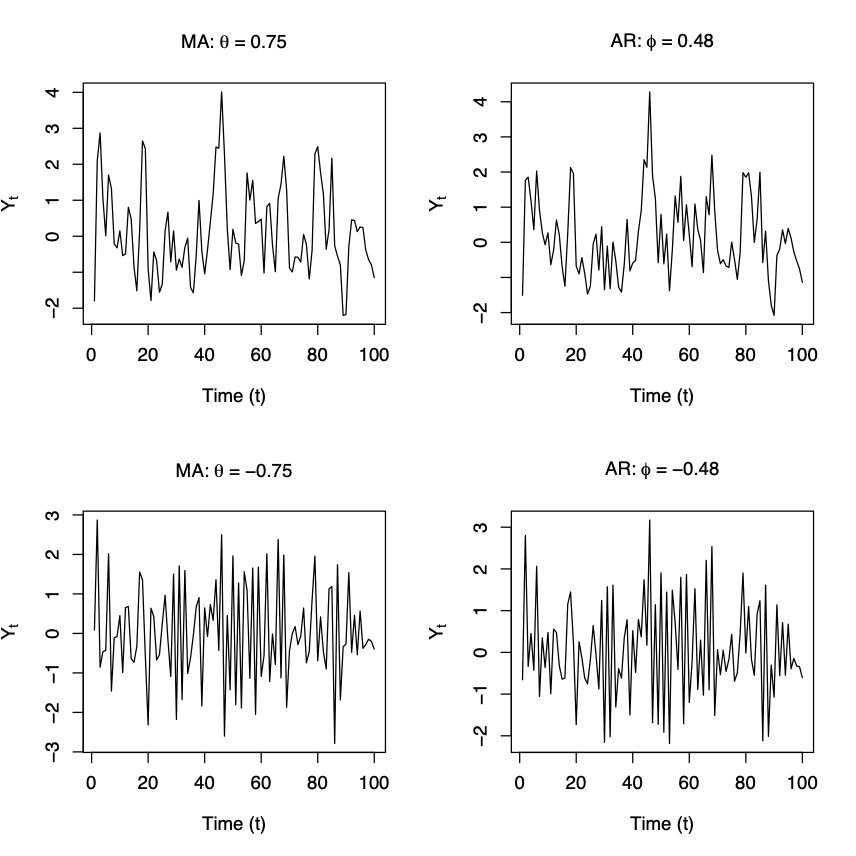
MA and AR processes: simulations
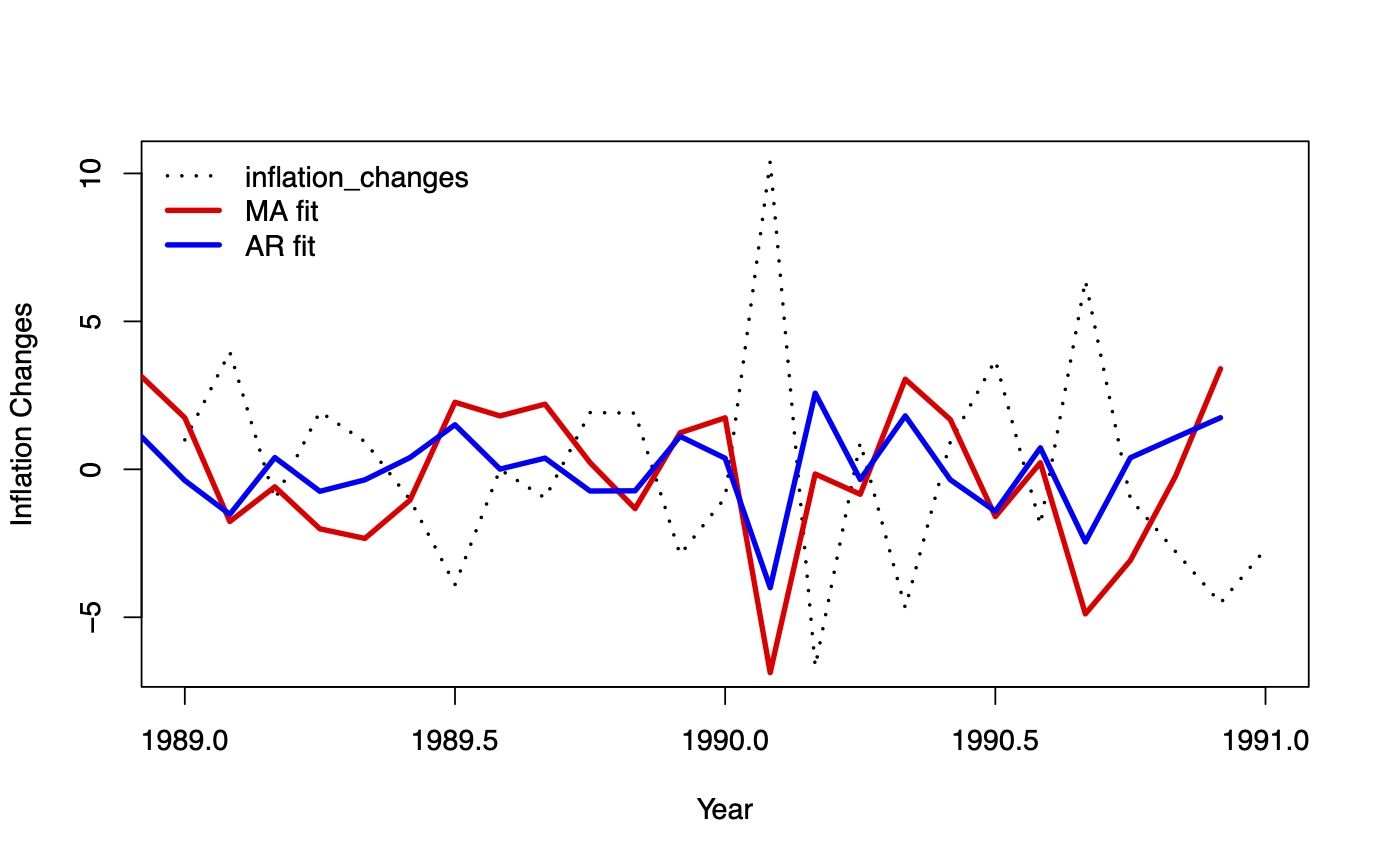
MA and AR processes: fitted values
- Changes in one-month US inflation rate
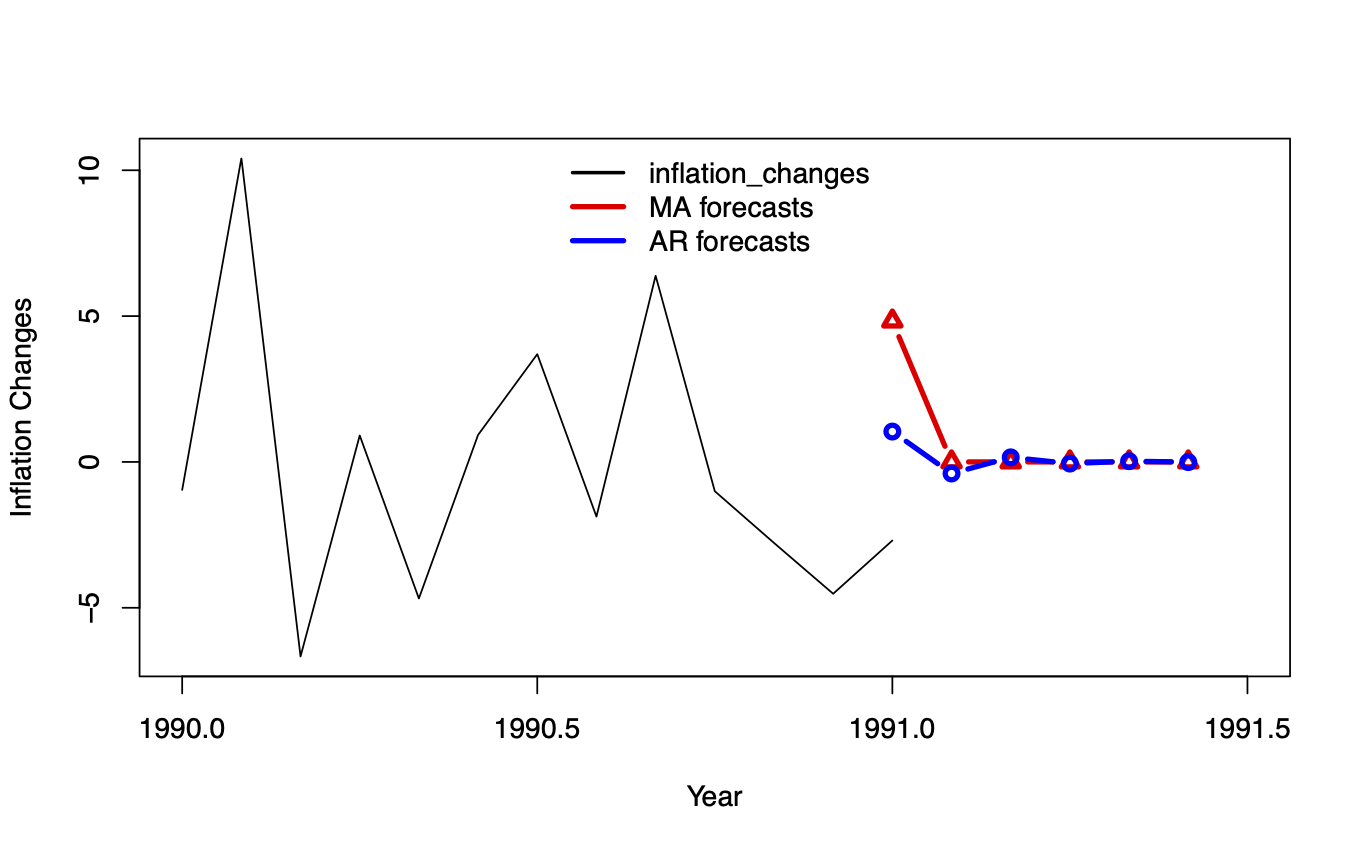
MA and AR processes: forecasts
- Changes in one-month US inflation rate
MA_inflation_changes <-
arima(inflation_changes,
order = c(0,0,1))
ma1 intercept
-0.7932 0.0010
s.e. 0.0355 0.0281
sigma^2 estimated as 8.882:
log likelihood = -1230.85,
aic = 2467.7
AIC(MA_inflation_changes)
BIC(MA_inflation_changes)
2467.703
2480.286
AR_inflation_changes <-
arima(inflation_changes,
order = c(1,0,0))
ar1 intercept
-0.3849 0.0038
s.e. 0.0420 0.1051
sigma^2 estimated as 10.37:
log likelihood = -1268.34,
aic = 2542.68
AIC(AR_inflation_changes)
BIC(AR_inflation_changes)
2542.679
2555.262
Let's practice!
Time Series Analysis in R

