The random walk (RW) model
Time Series Analysis in R

David S. Matteson
Associate Professor at Cornell University
Random walk
Random Walk (RW) is a simple example of a non-stationary process.
A random walk has:
- No specified mean or variance.
- Strong dependence over time.
- Its changes or increments are white noise (WN).
Random walk
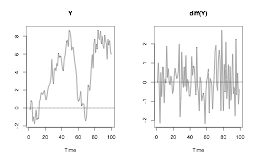
Time series plots of Random Walk:

Random walk
The random walk recursion:
$$Today = Yesterday + Noise$$
More formally:
$$ Y_t = Y_{t-1} + \epsilon_t$$
where $\epsilon_t$ is mean zero white noise (WN).
Simulation requires an initial point $Y_0$.
Only one parameter, the WN variance $\sigma^{2}_{\epsilon}$.
Random walk - I
The random walk process:
$$Y_t = Y_{t-1} + \epsilon_t$$
where $\epsilon_t$ is mean zero WN
As $Y_t - Y_{t-1} = \epsilon_t \rightarrow $ diff(Y) is WN
Random walk - II
Random walk with drift - I
The random walk with a drift:
$$Today = Constant + Yesterday + Noise$$
More formally: $$Y_t = c + Y_{t-1} + \epsilon_t$$
where $\epsilon_t$ is mean zero white noise (WN).
- Two parameters, the constant $c$ , and the WN variance $\sigma_{\epsilon}^2$.
- $Y_t - Y_{t-1} = $ ? $\rightarrow$ WN with mean $c$!
Random walk with drift - II
Time series plots of Random Walk with drift:
Let's practice!
Time Series Analysis in R

