AR model estimation and forecasting

Time Series Analysis in R

David S. Matteson

Associate Professor at Cornell University

AR processes: inflation rate

  • One-month US inflation rate (in percent, annual rate).
  • Monthly observations from 1950 through 1990
data(Mishkin, package = "Ecdat")

inflation <- as.ts(Mishkin[, 1])

ts.plot(inflation) ; acf(inflation)

Time Series Analysis in R

$$ (Today - Mean) = Slope * (Yesterday - Mean) + Noise $$

$$Y_t - \mu = \phi(Y_{t-1} - \mu) + \epsilon_t $$

$$\epsilon_t~ WhiteNoise(0, \sigma_{\epsilon}^2)$$

AR_inflation <- arima(inflation, order = c(1, 0, 0))

print(AR_inflation)

Coefficients:
        ar1  intercept
     0.5960     3.9745
s.e. 0.0364        0.3471
sigma^2 estimated as 9.713

ar1 = $ \hat{\phi}$, intercept = $ \hat{\mu} $, sigma^2 = $\hat{\sigma}^2_{\epsilon}$

Time Series Analysis in R

AR processes: fitted values - I

  • AR fitted values:

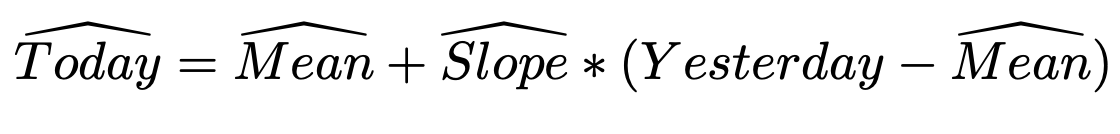
$$\hat{Y_t} = \hat{\mu} + \hat{\phi}(Y_{t-1} - \hat{\mu})$$

  • Residuals =

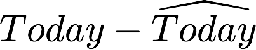
$$ \hat{\epsilon_t} = Y_t - \hat{Y_t}$$

Time Series Analysis in R

AR processes: fitted values - II

ts.plot(inflation)

AR_inflation_fitted <- inflation - residuals(AR_inflation)

points(AR_inflation_fitted, type = "l"
       col = "red", lty = 2)

Time Series Analysis in R

Forecasting

  • 1-step ahead forecasts
predict(AR_inflation)$pred 

Jan
1991 1.605797

predict(AR_inflation)$se

Jan
1991 3.116526
Time Series Analysis in R

Forecasting (cont.)

  • h-step ahead forecasts
predict(AR_inflation, n.ahead = 6)$pred

           Jan       Feb       Mar       Apr       May       Jun
1991  1.605797  2.562810  3.133165  3.473082  3.675664  3.796398

predict(AR_inflation, n.ahead = 6)$se

           Jan       Feb       Mar       Apr       May       Jun
1991  3.116526  3.628023  3.793136  3.850077  3.870101  3.877188
Time Series Analysis in R

Let's practice!

Time Series Analysis in R

Preparing Video For Download...