Correlations and t-tests

R For SAS Users

Melinda Higgins, PhD

Research Professor/Senior Biostatistician Emory University

Correlations compare SAS and R

sas proc corr like r psych corr.test function in r

sas and r codes for correlations

Correlations with psych package

# Correlations with psych::corr.test()
daviskeep %>%
  select(bmi, weight, height) %>%
  psych::corr.test()

Call:psych::corr.test(x = .)
Correlation matrix
        bmi weight height
bmi    1.00   0.88   0.38
weight 0.88   1.00   0.77
height 0.38   0.77   1.00
Sample Size
[1] 199
Probability values (Entries above the
diagonal are adjusted for multiple tests.)
       bmi weight height
bmi      0      0      0
weight   0      0      0
height   0      0      0

Scatterplot matrix SAS and R

plots matrix statement for sas proc corr and ggpairs from GGally package

sas and r codes for creating scatterplot matrix

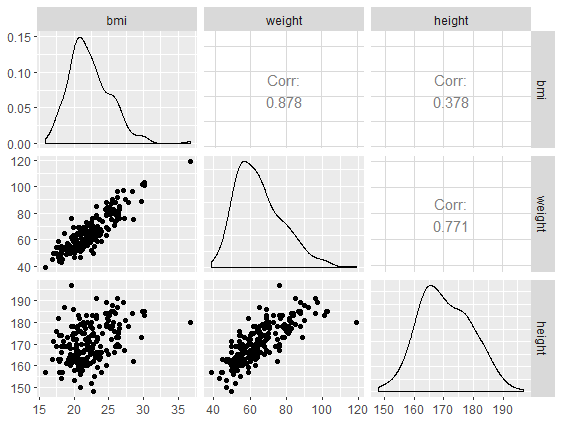
Scatterplot matrix - GGally::ggpairs() function

# Matrix plot with GGally::ggpairs()
daviskeep %>%
  select(bmi, weight, height) %>%
  GGally::ggpairs()

scatterplot matrix using ggpairs function from GGally package

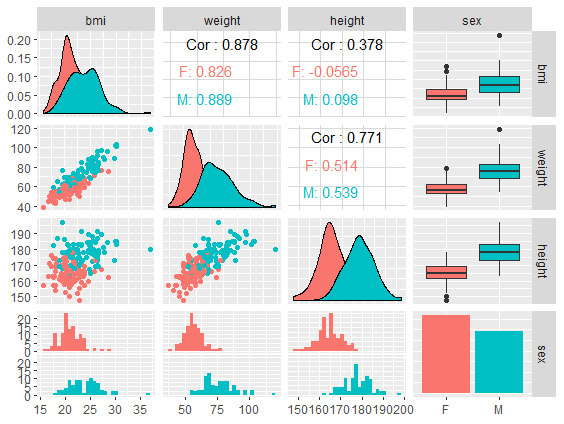
Scatterplot matrix - ggpairs by group

# Color points by sex group
daviskeep %>%
  select(bmi, weight, height, sex) %>%
  GGally::ggpairs(aes(color = sex))

scatterplot matrix using ggpairs function from GGally package by sex

Descriptive stats by group

No group counts

# Get mean and sd for bmi by sex
daviskeep %>% group_by(sex) %>%
  select(sex, bmi) %>%
  summarise(across(everything(),
                   list(mean = ~ mean(.x),
                        sd = ~ sd(.x))))

# A tibble: 2 × 3
  sex   bmi_mean bmi_sd
  <fct>    <dbl>  <dbl>
1 F         21.0   2.18
2 M         23.9   3.12

With group counts

# Add N = n(), get mean, sd for bmi by sex
daviskeep %>% group_by(sex) %>%
  select(sex, bmi) %>%
  summarise(across(everything(), 
                   list(mean = ~ mean(.x), 
                        sd = ~ sd(.x))),
            N = n())

# A tibble: 2 × 4
  sex   bmi_mean bmi_sd     N
  <fct>    <dbl>  <dbl> <int>
1 F         21.0   2.18   111
2 M         23.9   3.12    88

¹ https://dplyr.tidyverse.org/reference/context.html

T-tests SAS and R

sas proc ttest similar to using var.test and t.test r functions

sas and r codes for pooled and unpooled t-tests

T-tests - check for equal variances

# Perform equal variance test
var.test(bmi ~ sex, data = daviskeep)

    F test to compare two variances

data:  bmi by sex
F = 0.48637, num df = 110, denom df = 87, p-value = 0.0003668

alternative hypothesis: true ratio of variances is not equal to 1

95 percent confidence interval:
 0.3244691 0.7221946

sample estimates:
ratio of variances
         0.4863699

T-tests - pooled and unpooled

# UNPOOLED t-test bmi by sex
t.test(bmi ~ sex,
       data = daviskeep)

Welch Two Sample t-test

data:  bmi by sex
t = -7.5158, df = 149.45,
  p-value = 4.819e-12
alternative hypothesis: true difference
  in means is not equal to 0
95 percent confidence interval:
 -3.716353 -2.169035
sample estimates:
mean in group F mean in group M
       20.95632        23.89901

# POOLED t-test bmi by sex
t.test(bmi ~ sex, data = daviskeep,
       var.equal = TRUE)

    Two Sample t-test

data:  bmi by sex
t = -7.8239, df = 197,
  p-value = 3.055e-13
alternative hypothesis: true difference
  in means is not equal to 0
95 percent confidence interval:
 -3.684428 -2.200960
sample estimates:
mean in group F mean in group M
       20.95632        23.89901

Let's explore bivariate relationships in abalones!

R For SAS Users