Measuring Segregation: The Index of Dissimilarity

Analyzing US Census Data in Python

Lee Hachadoorian

Asst. Professor of Instruction, Temple University

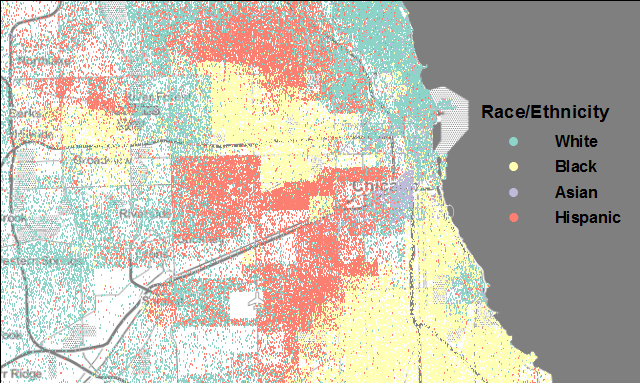
What is Segregation?

A dot density map of Chicago, showing White, Black, Asian, and Hispanic population in four different colors. Dots of the same color are clustered near each other, implying a landscape segregated by race.

Index of Dissimilarity Formula

Given two groups A and B:

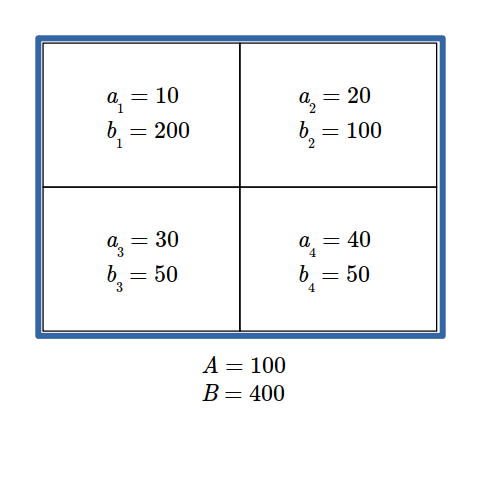
A box divided into four quadrants, showing populations of A and B in each quadrant.

Index of Dissimilarity Formula

Given two groups A and B:

$$\color{white}{D = {\frac{1}{2}\sum_i}\color{white}{\left\lvert \frac{a_i}{A} - \frac{b_i}{B} \right\rvert}}$$

$a_i$ = Small area Group A count
$b_i$ = Small area Group B count

A box divided into four quadrants, showing populations of A and B in each quadrant.

Index of Dissimilarity Formula

Given two groups A and B:

$$\color{white}{D = {\frac{1}{2}\sum_i}\color{white}{\left\lvert \frac{a_i}{A} - \frac{b_i}{B} \right\rvert}}$$

$a_i$ = Small area Group A count
$b_i$ = Small area Group B count
$A$ = Large area Group A count
$B$ = Large area Group B count

A box divided into four quadrants, showing populations of A and B in each quadrant.

Index of Dissimilarity Formula

Given two groups A and B:

$$\color{red}D = \frac{1}{2}\sum_i{\left\lvert \frac{{a_i}}{A} - \frac{b_i}{B} \right\rvert}$$

$a_i$ = Small area Group A count
$b_i$ = Small area Group B count
$A$ = Large area Group A count
$B$ = Large area Group B count

A box divided into four quadrants, showing populations of A and B in each quadrant.

Index of Dissimilarity Formula

Given two groups A and B:

$$D = \color{white}{\frac{1}{2}\sum_i}\color{white}{\left\lvert \color{red}{\frac{a_i}{A}} \color{white}{- \frac{b_i}{B}} \right\rvert}$$

$a_i$ = Small area Group A count
$b_i$ = Small area Group B count
$A$ = Large area Group A count
$B$ = Large area Group B count

A box divided into four quadrants, showing populations of A and B in each quadrant.

Index of Dissimilarity Formula

Given two groups A and B:

$$D = \color{white}{\frac{1}{2}\sum_i}\color{white}{\left\lvert \frac{a_i}{A} - \color{red}{\frac{b_i}{B}} \right\rvert}$$

$a_i$ = Small area Group A count
$b_i$ = Small area Group B count
$A$ = Large area Group A count
$B$ = Large area Group B count

A box divided into four quadrants, showing populations of A and B in each quadrant.

Index of Dissimilarity Formula

Given two groups A and B:

$$D = \color{white}{\frac{1}{2}\sum_i}\color{red}{\left\lvert \frac{a_i}{A} - \frac{b_i}{B} \right\rvert}$$

$a_i$ = Small area Group A count
$b_i$ = Small area Group B count
$A$ = Large area Group A count
$B$ = Large area Group B count

A box divided into four quadrants, showing populations of A and B in each quadrant.

Index of Dissimilarity Formula

Given two groups A and B:

$$D = \color{white}{\frac{1}{2}}\color{red}{\sum_i}{\left\lvert \frac{a_i}{A} - \frac{b_i}{B} \right\rvert}$$

$a_i$ = Small area Group A count
$b_i$ = Small area Group B count
$A$ = Large area Group A count
$B$ = Large area Group B count

A box divided into four quadrants, showing populations of A and B in each quadrant.

Index of Dissimilarity Formula

Given two groups A and B:

$$D = \color{red}{\frac{1}{2}}\sum_i{\left\lvert \frac{a_i}{A} - \frac{b_i}{B} \right\rvert}$$

$a_i$ = Small area Group A count
$b_i$ = Small area Group B count
$A$ = Large area Group A count
$B$ = Large area Group B count

A box divided into four quadrants, showing populations of A and B in each quadrant.

Index of Dissimilarity Formula

Given two groups A and B:

$$D = \frac{1}{2}\sum_i{\left\lvert \frac{a_i}{A} - \frac{b_i}{B} \right\rvert}$$

$a_i$ = Small area Group A count
$b_i$ = Small area Group B count
$A$ = Large area Group A count
$B$ = Large area Group B count

A box divided into four quadrants, showing populations of A and B in each quadrant.

Suitable Data

tracts.head()

  state county   tract  white  black
0    01    001  020100   1601    217
1    01    001  020200    844   1214
2    01    001  020300   2538    647
3    01    001  020400   4030    191
4    01    001  020500   8438   1418

Source: Table P5 - 2010 Decennial Census

white = Nonhispanic White population
black = Nonhispanic Black population

Calculating the Index of Dissimilarity (D)

# Extract California tracts using state FIPS "06"
ca_tracts = tracts[tracts["state"] == "06"]

# Define convenience variables to hold column names
w = "white"
b = "black"

Calculating the Index of Dissimilarity (D)

# Print the sum of Black population for all tracts in California
print(ca_tracts[b].sum())

# Print the sum of White population for all tracts in California
print(ca_tracts[w].sum())

14956253

Calculating the Index of Dissimilarity (D)

$$D = \frac{1}{2}\sum_i{\left\lvert \frac{a_i}{A} - \frac{b_i}{B} \right\rvert}$$

# Calculate Index of Dissimilarity
print(0.5 * sum(abs(
  ca_tracts[w] / ca_tracts[w].sum() - ca_tracts[b] / ca_tracts[b].sum()
  )))

0.6033425039167011

Let's Practice!

Analyzing US Census Data in Python

Preparing Video For Download...