Geometric distributions
Foundations of Probability in Python

Alexander A. Ramírez M.
CEO @ Synergy Vision
Geometric modeling

Geometric parameter
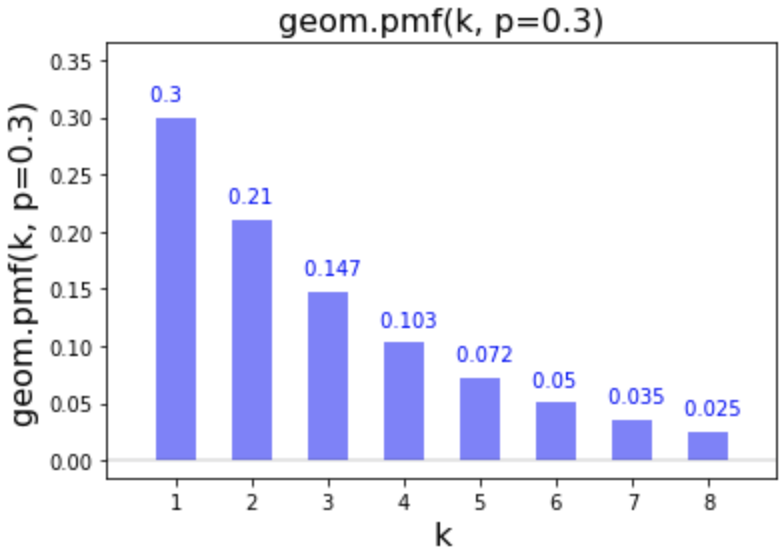
Model for a basketball player with probability 0.3 of scoring.
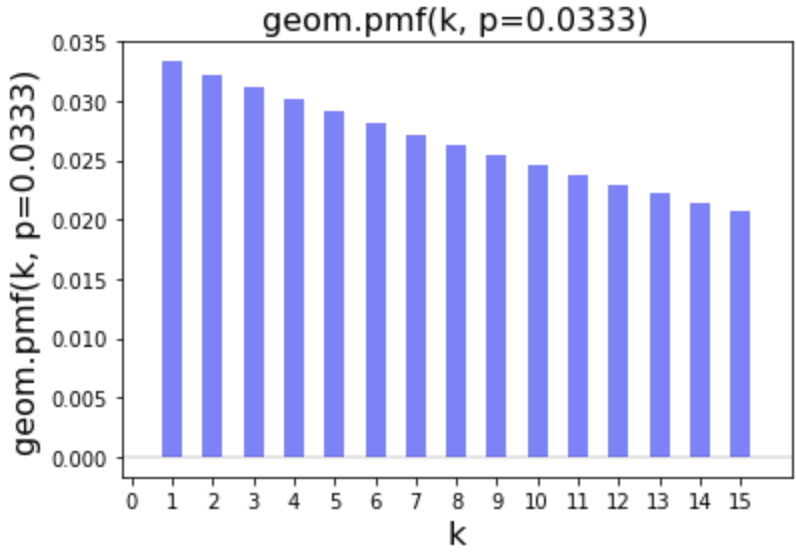
We can model a grizzly bear that has a 0.033 probability of catching a salmon.
Probability mass function (pmf)

In Python we code this as follows:
# Import geom
from scipy.stats import geom
# Calculate the probability mass
# with pmf
geom.pmf(k=30, p=0.0333)
0.02455102908739612
p parameter specifies probability of success.
Cumulative distribution function (cdf)
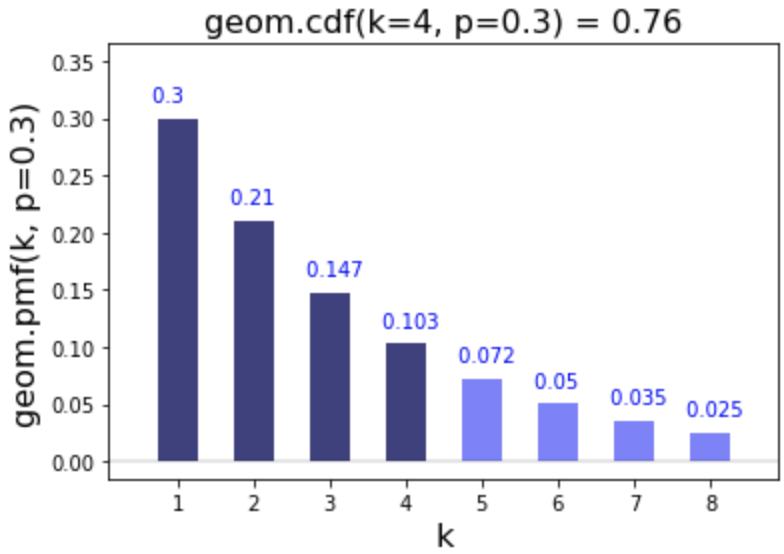
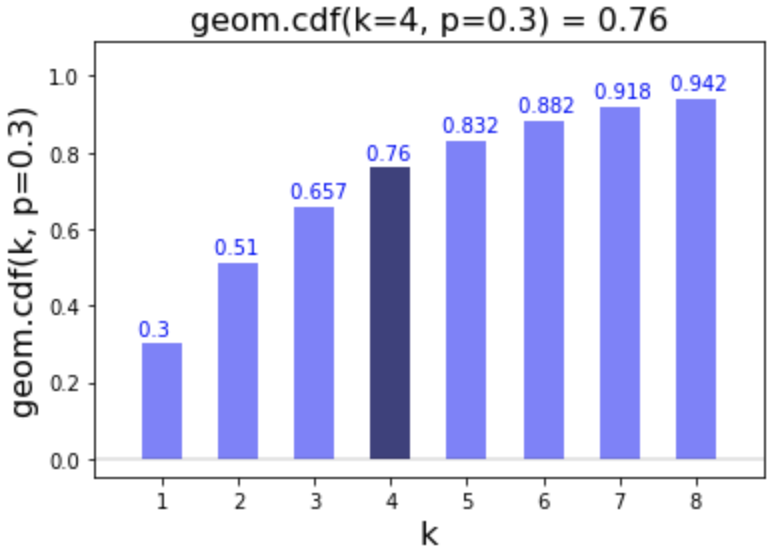
# Calculate cdf of 4
geom.cdf(k=4, p=0.3)
0.7598999999999999
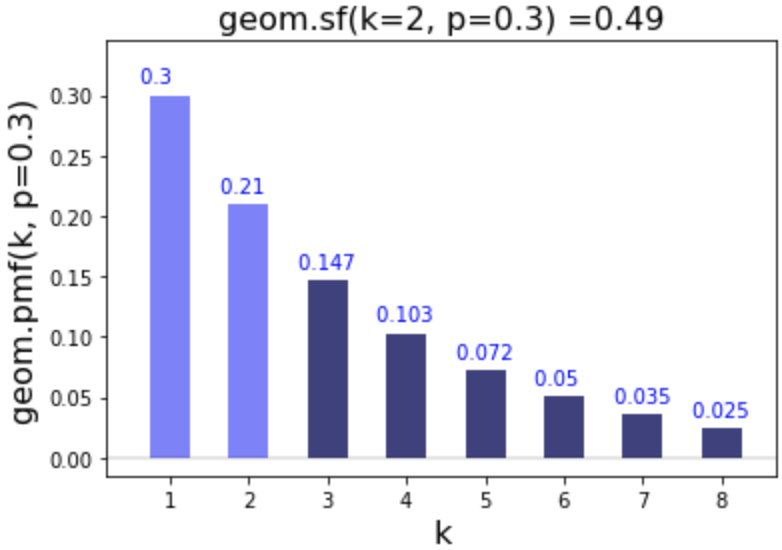
Survival function (sf)
$$ $$
# Calculate sf of 2
geom.sf(k=2, p=0.3)
0.49000000000000005
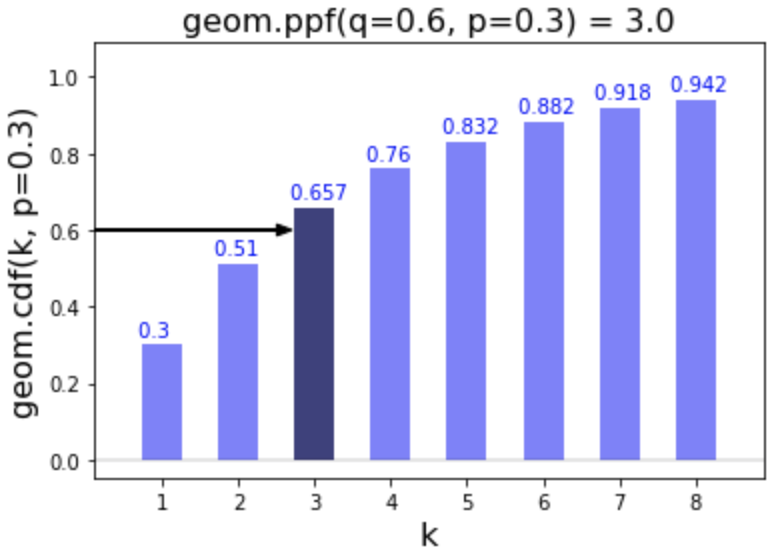
Percent point function (ppf)
$$ $$
# Calculate ppf of 0.6
geom.ppf(q=0.6, p=0.3)
3.0
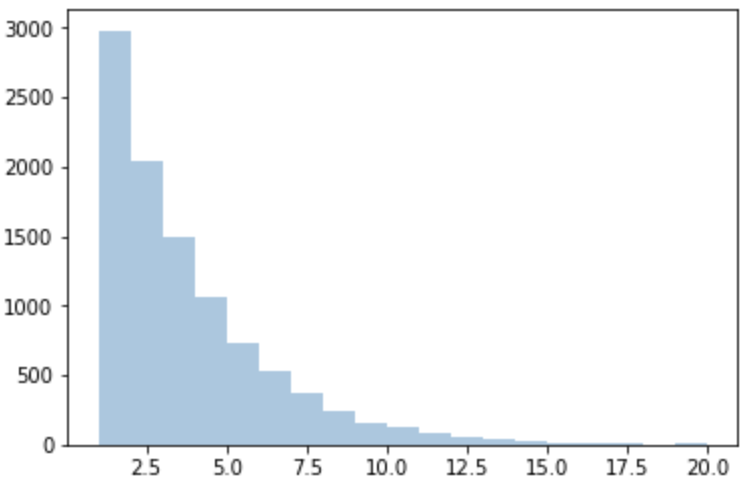
Sample generation (rvs)
# Import poisson, matplotlib.pyplot, and seaborn
from scipy.stats import geom
import matplotlib.pyplot as plt
import seaborn as sns
# Create the sample using geom.rvs()
sample = geom.rvs(p=0.3, size=10000, random_state=13)
# Plot the sample
sns.distplot(sample, bins = np.linspace(0,20,21), kde=False)
plt.show()
Sample generation (rvs) (Cont.)
Let's go try until we succeed!
Foundations of Probability in Python

