Probability mass and distribution functions

Foundations of Probability in Python

Alexander A. Ramírez M.

CEO @ Synergy Vision

Probability mass function (pmf)

$$ $$

$$ binomial.pmf(k, n, p) = \binom{n}{k}p^k(1-p)^{n-k} $$

$$ $$

$$ binomial.pmf(k, n, p) = \color{red}{\binom{n}{k}}p^k(1-p)^{n-k} $$

$$ $$

$$ binomial.pmf(k, n, p) = \binom{n}{k}\color{red}{p^k}(1-p)^{n-k} $$

$$ $$

$$ binomial.pmf(k, n, p) = \binom{n}{k}p^k\color{red}{(1-p)^{n-k}} $$

Probability mass function for binomial distribution for 10 flips and fair coin

$$ $$

$$ binomial.pmf(k, n, p) = \binom{n}{k}p^k(1-p)^{n-k} $$

In Python:

binom.pmf(k, n, p)

# Probability of 2 heads after 10 throws with a fair coin
binom.pmf(k=2, n=10, p=0.5)

0.04394531249999999

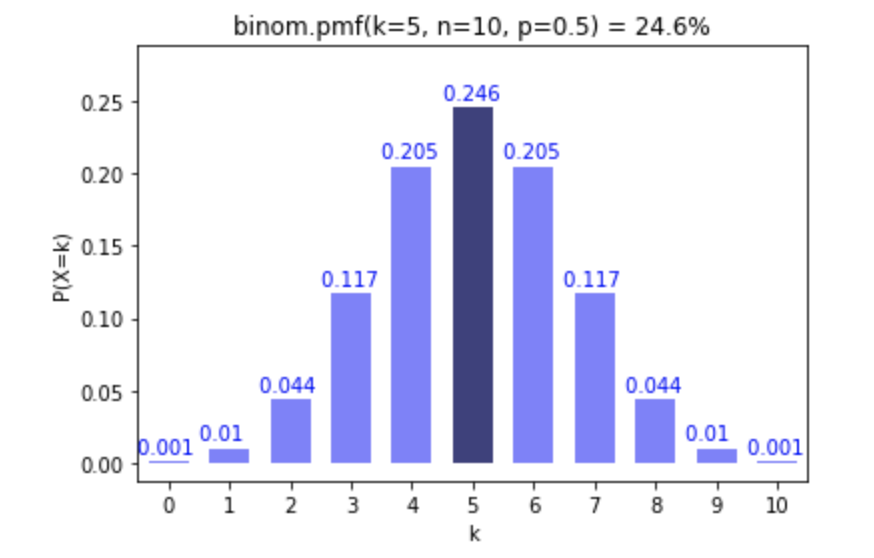
# Probability of 5 heads after 10 throws with a fair coin
binom.pmf(k=5, n=10, p=0.5)

0.24609375000000025

# Probability of 50 heads after 100 throws with p=0.3
binom.pmf(k=50, n=100, p=0.3)

1.3026227131445298e-05

# Probability of 65 heads after 100 throws with p=0.7
binom.pmf(k=65, n=100, p=0.7)

0.0467796823527298

$$ $$

$$ binomial.cdf(k, n, p) = \binom{n}{0}p^0(1-p)^{n} + \binom{n}{1}p(1-p)^{n-1} + ... + \binom{n}{k}p^k(1-p)^{n-k} $$

$$ $$

$$ binomial.cdf(k, n, p) = \color{red}{\binom{n}{0}p^0(1-p)^{n}} + \binom{n}{1}p(1-p)^{n-1} + ... + \binom{n}{k}p^k(1-p)^{n-k} $$

$$ $$

$$ binomial.cdf(k, n, p) = \binom{n}{0}p^0(1-p)^{n} + \color{red}{\binom{n}{1}p(1-p)^{n-1}} + ... + \binom{n}{k}p^k(1-p)^{n-k} $$

$$ $$

$$ binomial.cdf(k, n, p) = \binom{n}{0}p^0(1-p)^{n} + \binom{n}{1}p(1-p)^{n-1} + ... + \color{red}{\binom{n}{k}p^k(1-p)^{n-k}} $$

$$ $$ Probability mass function for binomial distribution for 10 flips and fair coin

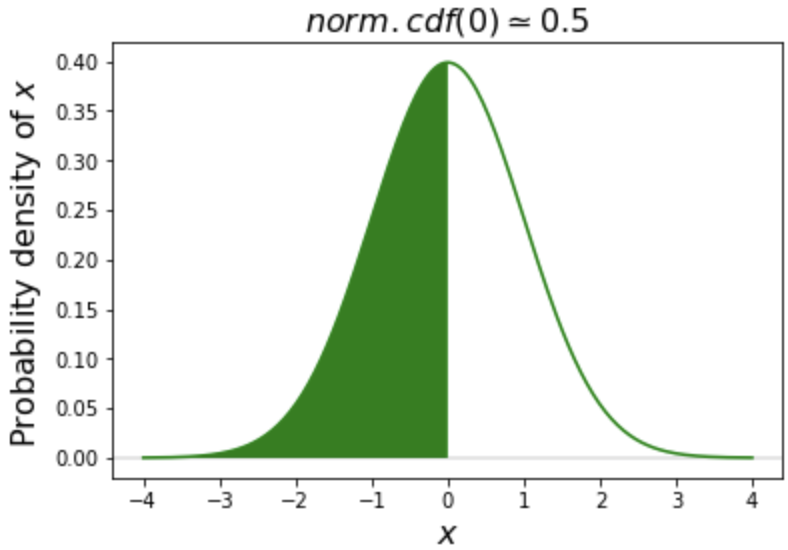
$$ $$ Normal Cumulative distribution function

$$ $$ $$ binomial.cdf(k, n, p) = \binom{n}{0}p^0(1-p)^{n} + \binom{n}{1}p(1-p)^{n-1} + ... + \binom{n}{k}p^k(1-p)^{n-k} $$

In Python:

binom.cdf(k=1, n=3, p=0.5)

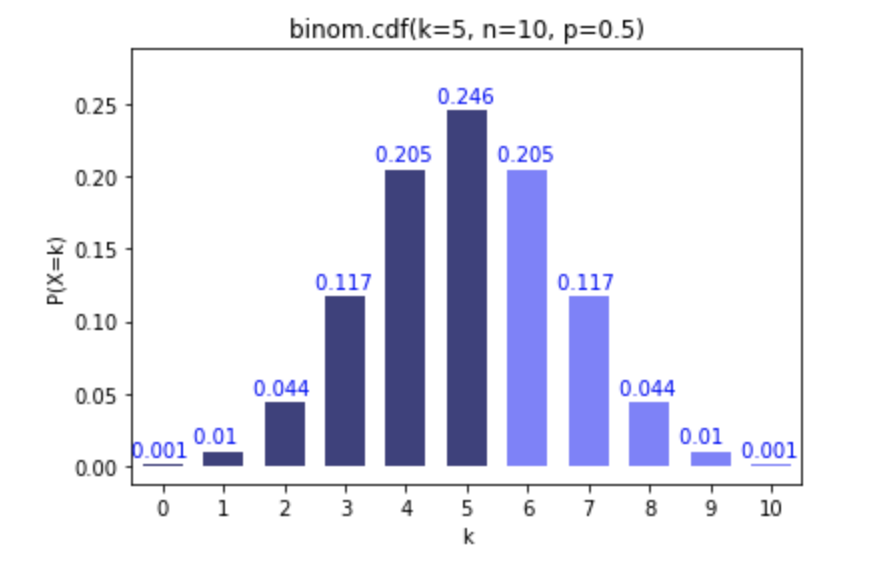
# Probability of 5 heads or less after 10 throws with a fair coin
binom.cdf(k=5, n=10, p=0.5)

0.6230468749999999

# Probability of 50 heads or less after 100 throws with p=0.3
binom.cdf(k=50, n=100, p=0.3)

0.9999909653138043

# Probability of more than 59 heads after 100 throws with p=0.7
1-binom.cdf(k=59, n=100, p=0.7)

0.9875015928335618

# Probability of more than 59 heads after 100 throws with p=0.7
binom.sf(k=59, n=100, p=0.7)

0.9875015928335618

Foundations of Probability in Python