Bayes' rule

Foundations of Probability in Python

Alexander A. Ramírez M.

CEO @ Synergy Vision

Probability of two coin flips

P(A and B) for independent events

$$ $$

$$\color{red}{P(A\ and\ B)=P(A)P(B)}$$

P(A and B) for dependent events

$$ $$

$$P(A\ and\ B)=P(A)P(B)$$ $$P(A\ and\ B)=\color{blue}{P(A)P(B|A)}$$

P(A and B) for dependent events (Cont.)

$$ $$

$$P(A\ and\ B)=P(A)P(B)$$ $$P(A\ and\ B)=P(A)P(B|A)$$ $$P(B\ and\ A)=\color{red}{P(B)P(A|B)}$$

P(A and B) is equal to P(B and A)

$$ $$

$$P(A\ and\ B)=P(A)P(B)$$ $$\color{gray}{P(A\ and\ B)}=\color{blue}{P(A)P(B|A)}$$ $$\color{gray}{P(B\ and\ A)}=\color{red}{P(B)P(A|B)}$$

P(A and B) is equal to P(B and A) (Cont.)

$$ $$

$$P(A\ and\ B)=P(A)P(B)$$ $$\color{gray}{P(A\ and\ B)}=\color{blue}{P(A)P(B|A)}$$ $$\color{gray}{P(B\ and\ A)}=\color{red}{P(B)P(A|B)}$$ $$\color{blue}{P(A)P(B|A)}=\color{gray}{P(A\ and\ B)}=\color{gray}{P(B\ and\ A)}=\color{red}{P(B)P(A|B)}$$

Bayes' relation

$$ $$

Bayes' rule

$$ $$

$$\color{blue}{P(A)P(B|A)}=\color{red}{P(B)P(A|B)}$$ $$ $$ $$\Longrightarrow \large{\color{red}{P(A|B)} = \frac{\color{blue}{P(A)P(B|A)}}{\color{red}{P(B)}}}$$

Total probability

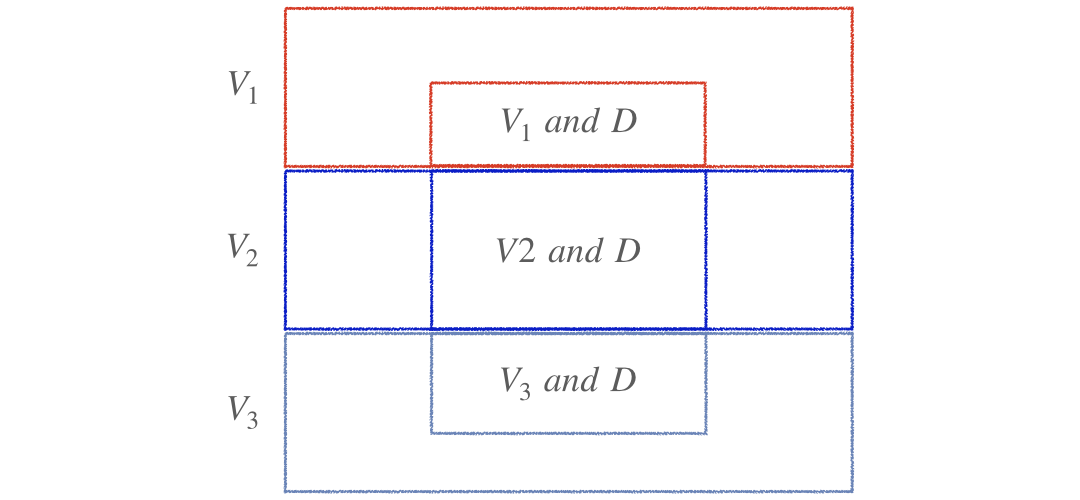
Damaged parts from all vendors in a Venn diagram

$$P(D) = P(V_1\ and\ D) + P(V_2\ and\ D) + P(V_3\ and\ D)$$

Total probability (Cont.)

$$ $$ $$P(D) = \color{red}{P(V_1\ and\ D)} + \color{blue}{P(V_2\ and\ D)} + \color{#9FAAC3}{P(V_3\ and\ D)}$$

$$\color{red}{P(V_1\ and\ D)} = \color{red}{P(V_1)P(D|V_1)}$$ $$\color{blue}{P(V_2\ and\ D)} = \color{blue}{P(V_2)P(D|V_2)}$$ $$\color{#9FAAC3}{P(V_3\ and\ D)} = \color{#9FAAC3}{P(V_3)P(D|V_3)}$$

$$P(D)=\color{red}{P(V_1)P(D|V_1)}+\color{blue}{P(V_2)P(D|V_2)}+\color{#9FAAC3}{P(V_3)P(D|V_3)}$$

Total probability (Cont.)

Damaged parts from all vendors in a Venn diagram

$$P(D)=\color{red}{P(V_1)P(D|V_1)}+\color{blue}{P(V_2)P(D|V_2)}+\color{#9FAAC3}{P(V_3)P(D|V_3)}$$

Bayes' formula

$$P(A|B) = \frac{P(A)P(B|A)}{P(B)}$$

Bayes' formula (Cont.)

Bayes' formula:

$$P(A|B) = \frac{P(A)P(B|A)}{P(B)}$$

The probability of a part being from vendor i, given that it is damaged:

$$P(V_i|D) = \frac{P(V_i)P(D|V_i)}{P(D)}$$

Bayes' formula (Cont.)

Bayes' formula: $$P(A|B) = \frac{P(A)P(B|A)}{P(B)}$$
The probability of a part being from vendor i, given that it is damaged:

$$P(V_i|D) = \frac{P(V_i)P(D|V_i)}{P(D)}$$ $$ $$ $$P(V_1|D) = \frac{P(V_1)P(D|V_1)}{P(V_1)P(D|V_1)+P(V_2)P(D|V_2)+P(V_3)P(D|V_3)}$$

Visual representation of Bayes' rule

Damaged parts from all vendors in a Venn diagram

$$P(V_1|D) = \frac{P(V_1)P(D|V_1)}{P(V_1)P(D|V_1)+P(V_2)P(D|V_2)+P(V_3)P(D|V_3)}$$

Visual representation of Bayes' rule (Cont.)

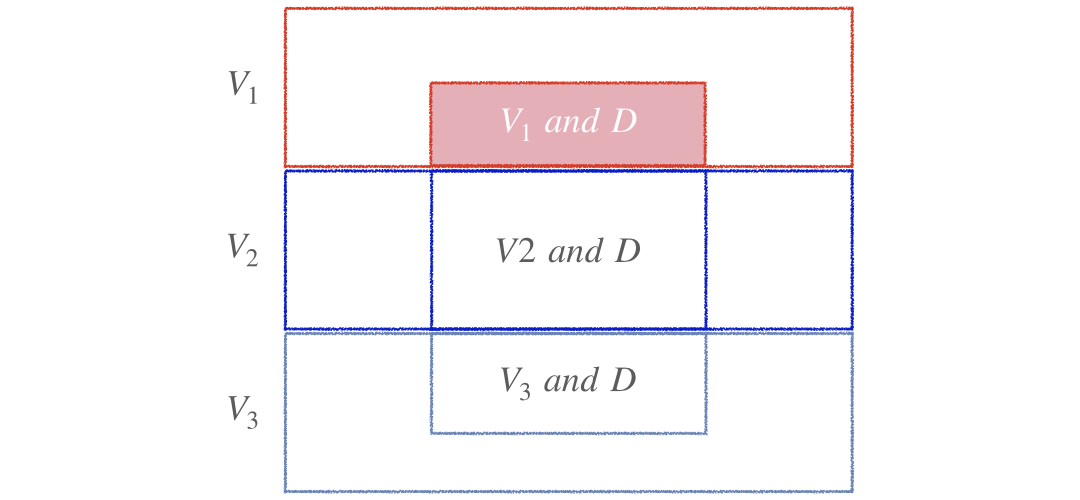
Damaged parts from vendor 1 in a Venn diagram

$$P(V_1|D) = \frac{\color{red}{P(V_1)P(D|V_1)}}{P(V_1)P(D|V_1)+P(V_2)P(D|V_2)+P(V_3)P(D|V_3)}$$

Visual representation of Bayes' rule (Cont.)

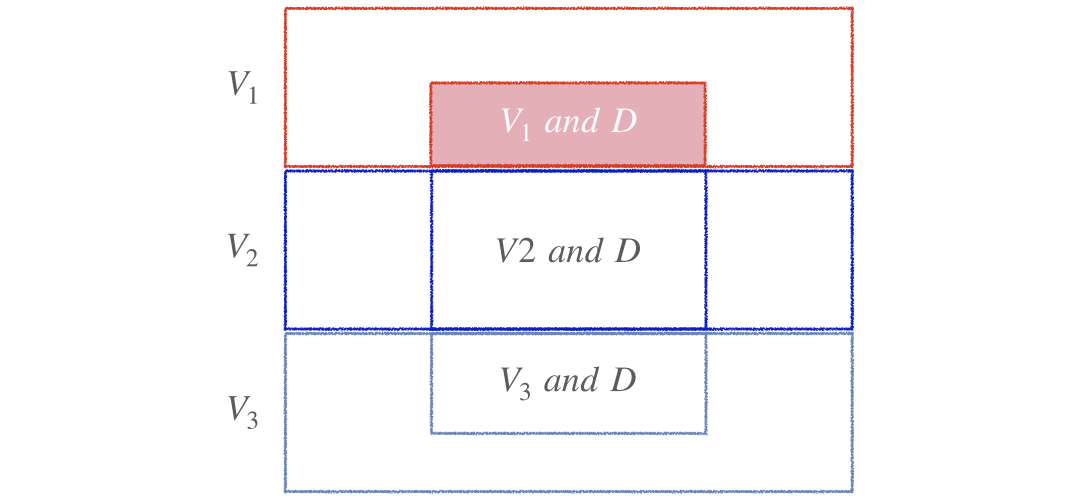
Damaged parts from vendor 1 in a Venn diagram

$$P(V_1|D) = \frac{P(V_1)P(D|V_1)}{\color{red}{P(V_1)P(D|V_1)}+P(V_2)P(D|V_2)+P(V_3)P(D|V_3)}$$

Visual representation of Bayes' rule (Cont.)

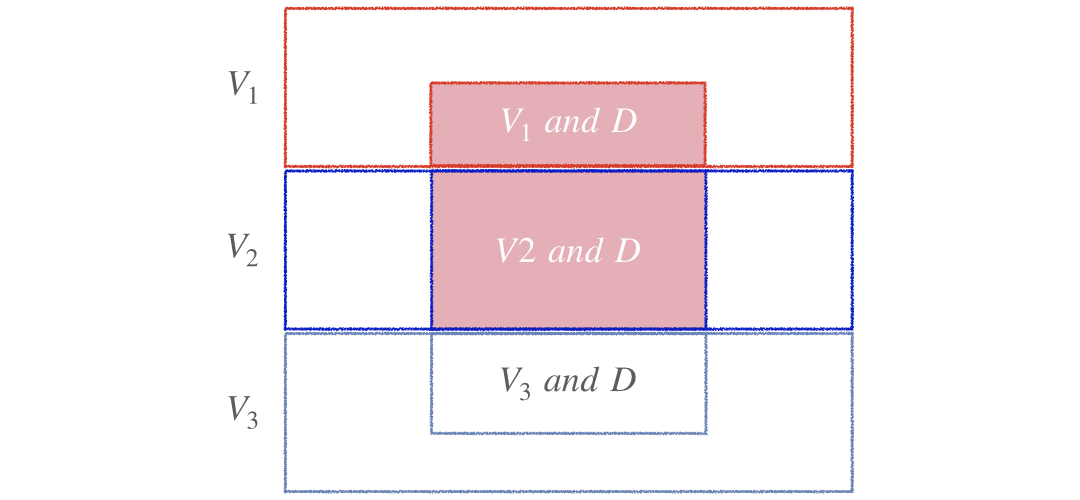
Damaged parts from vendor 1 and 2 in a Venn diagram

$$P(V_1|D) = \frac{P(V_1)P(D|V_1)}{P(V_1)P(D|V_1)+\color{red}{P(V_2)P(D|V_2)}+P(V_3)P(D|V_3)}$$

Visual representation of Bayes' rule (Cont.)

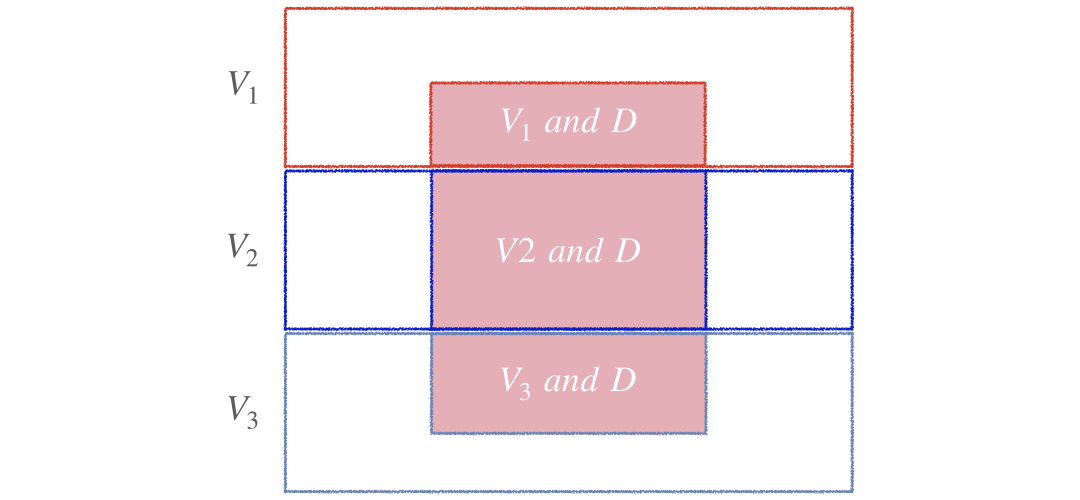
Damaged parts from vendor 1, 2 and 3 in a Venn diagram

$$P(V_1|D) = \frac{P(V_1)P(D|V_1)}{P(V_1)P(D|V_1)+P(V_2)P(D|V_2)+\color{red}{P(V_3)P(D|V_3)}}$$

Visual representation of Bayes' rule (Cont.)

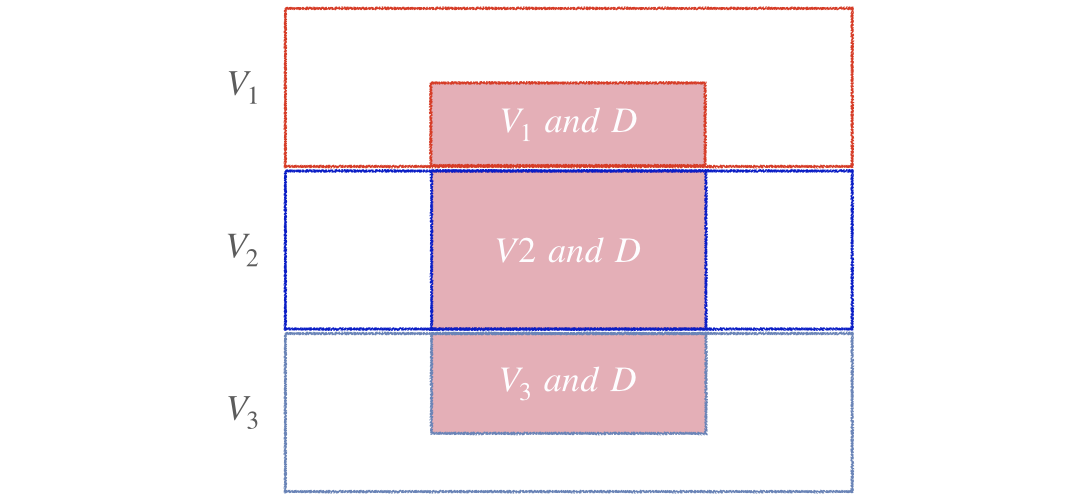
Damaged parts from vendor 1, 2 and 3 in a Venn diagram

$$P(V_1|D) = \frac{P(V_1)P(D|V_1)}{P(V_1)P(D|V_1)+P(V_2)P(D|V_2)+P(V_3)P(D|V_3)}$$

Visual representation of Bayes' rule (Cont.)

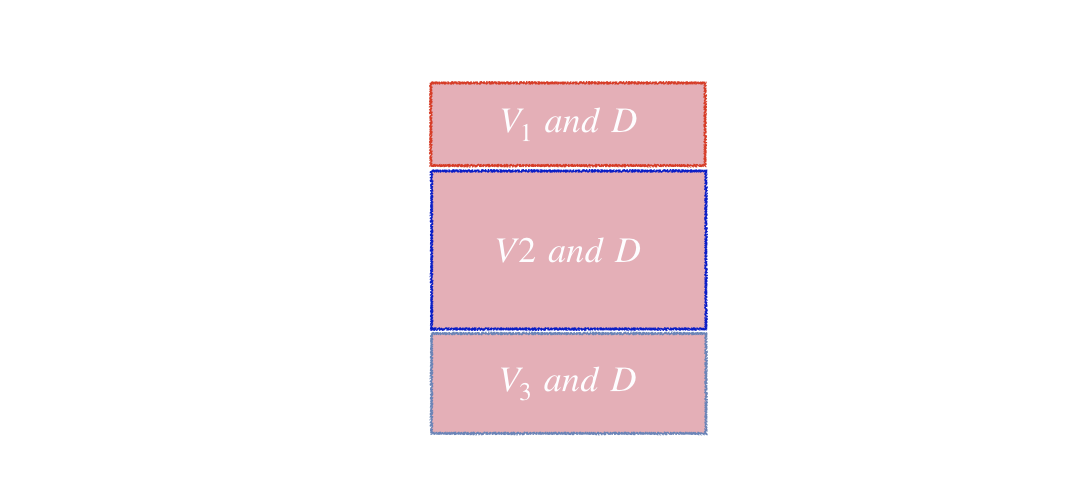
Damaged parts from vendor 1, 2 and 3 in a Venn diagram

$$P(V_1|D) = \frac{P(V_1)P(D|V_1)}{P(V_1)P(D|V_1)+P(V_2)P(D|V_2)+P(V_3)P(D|V_3)}$$

Visual representation of Bayes' rule (Cont.)

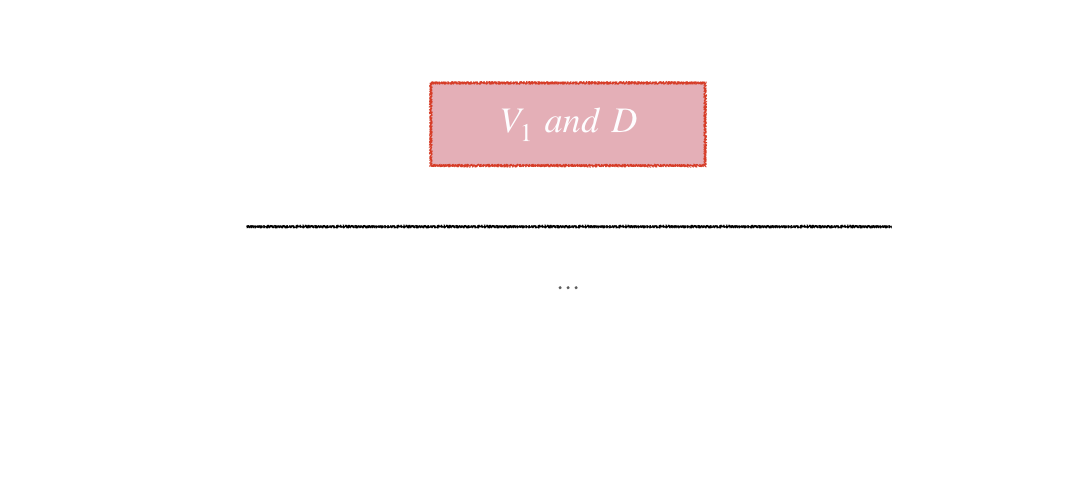
Damaged parts from vendor 1 over damaged parts from vendor 1, 2 and 3 in a Venn diagram

$$P(V_1|D) = \frac{\color{red}{P(V_1)P(D|V_1)}}{...}$$

Visual representation of Bayes' rule (Cont.)

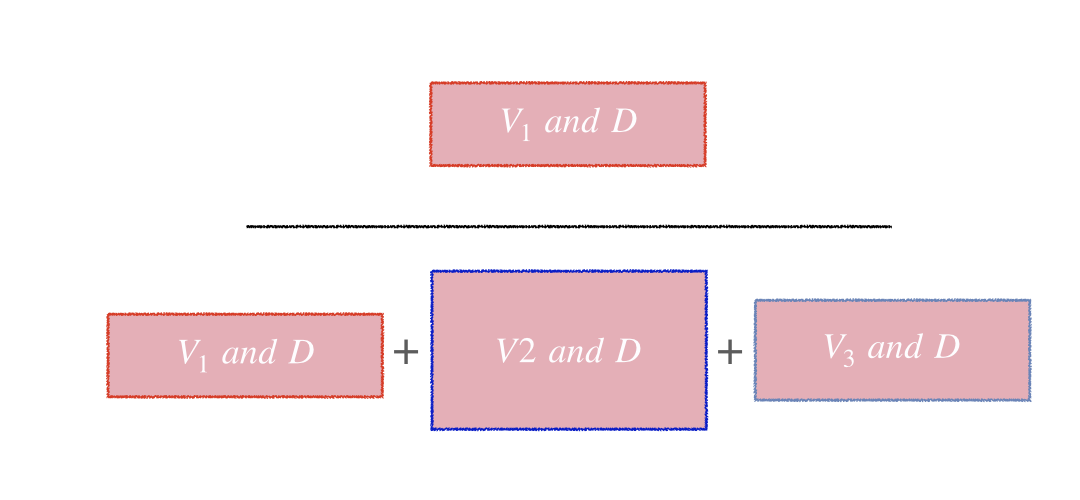
Damaged parts from vendor 1 over damaged parts from vendor 1, 2 and 3 in a Venn diagram

$$P(V_1|D) = \frac{\color{red}{P(V_1)P(D|V_1)}}{\color{red}{P(V_1)P(D|V_1)}+\color{blue}{P(V_2)P(D|V_2)}+\color{#9FAAC3}{P(V_3)P(D|V_3)}}$$

Factories and parts example in Python

A certain electronic part is manufactured by three different vendors, V1, V2, and V3.

Half of the parts are produced by V1, and V2 and V3 each produce 25%. The probability of a part being damaged given that it was produced by V1 is 1%, while it's 2% for V2 and 3% for V3.

Given that the part is damaged, what is the probability that it was manufactured by V1?

Factories and parts example in Python (Cont.)

Given that the part is damaged, get the probability that it was manufactured by V1.

P_V1 = 0.5
P_V2 = 0.25
P_V3 = 0.25

P_D_g_V1 = 0.01
P_D_g_V2 = 0.02
P_D_g_V3 = 0.03

P_Damaged = P_V1 * P_D_g_V1 + P_V2 * P_D_g_V2 + P_V3 * P_D_g_V3

Factories and parts example in Python (Cont.)

P_V1_g_D = (P_V1 * P_D_g_V1) / P_Damaged # P(V1|D) calculation
print(P_V1_g_D)

A randomly selected part which is damaged is manufactured by V1 with probability:

0.285714285714

Let's exercise with Bayes

Foundations of Probability in Python