Normal probabilities

Foundations of Probability in Python

Alexander A. Ramírez M.

CEO @ Synergy Vision

Probability density

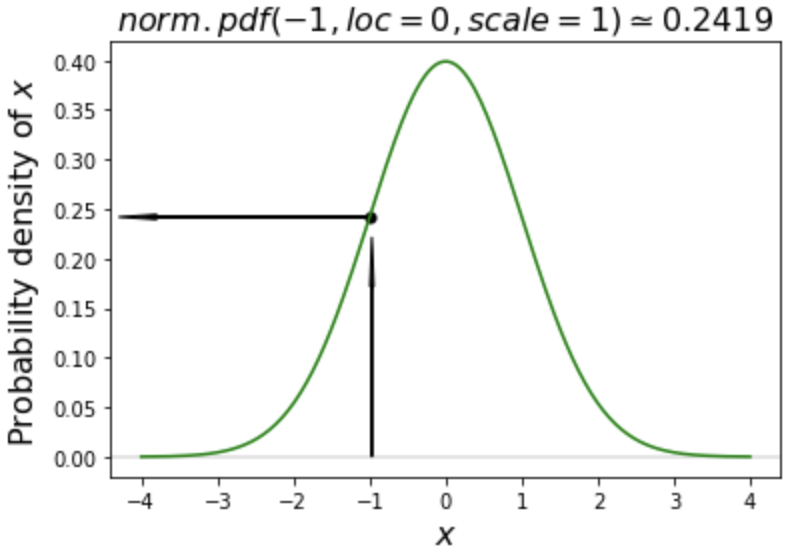
$$ $$ Plot of probability density of -1

In Python this can be done in a couple of lines:

# Import norm
from scipy.stats import norm

# Calculate the probability density 
# with pdf
norm.pdf(-1, loc=0, scale=1)

0.24197072451914337

loc parameter specifies the mean and scale parameter specifies the standard deviation.

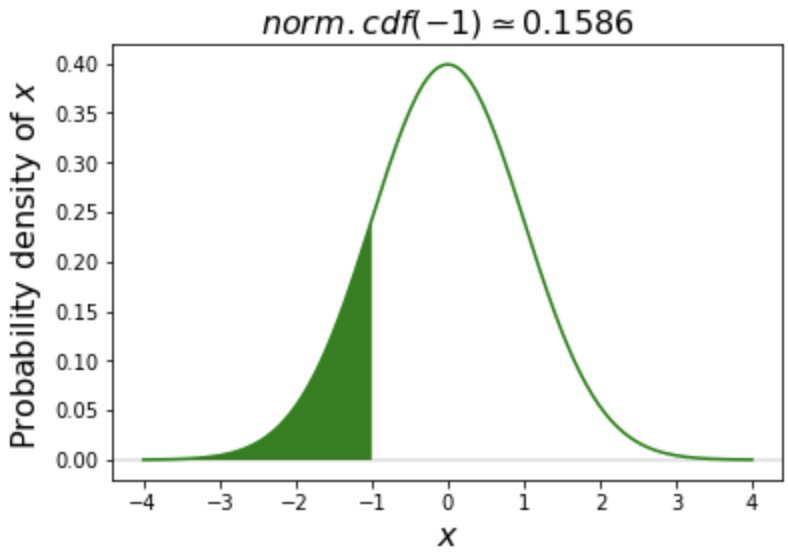
$$ $$ Cumulative distribution function of -1 in density plot

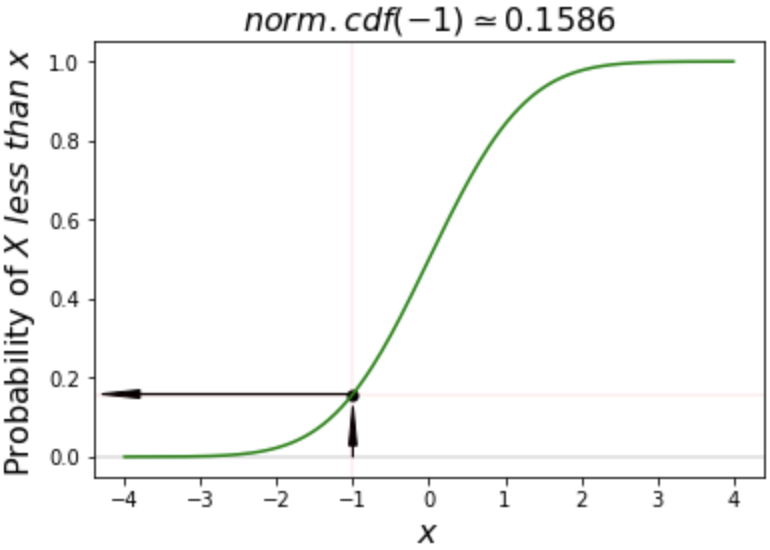
$$ $$ Plot of cumulative distribution function of -1

$$ $$ Plot of probability density function less than 1.5

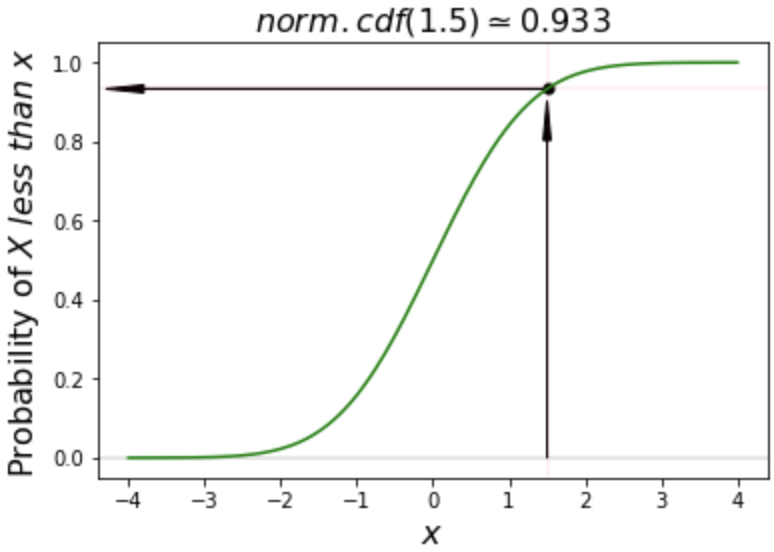
$$ $$ Plot of cumulative distribution function for 1.5

$$ $$ Plot of probability density function less than 5

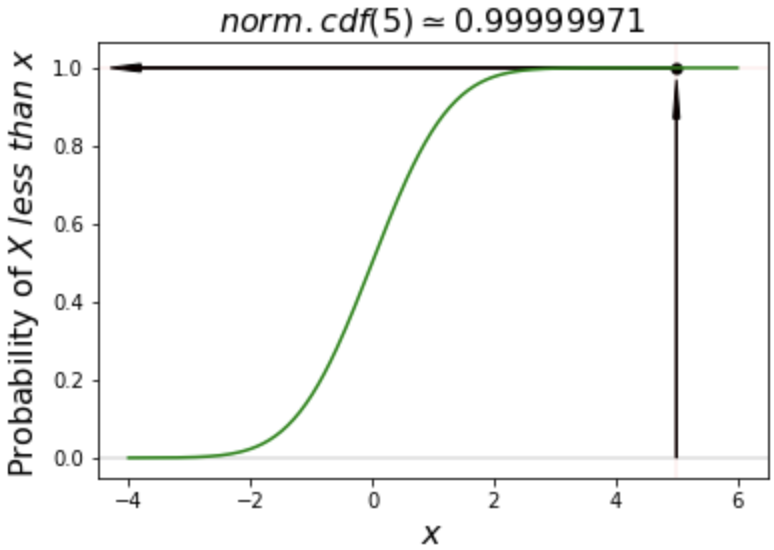
$$ $$ Plot of cumulative distribution function for 5

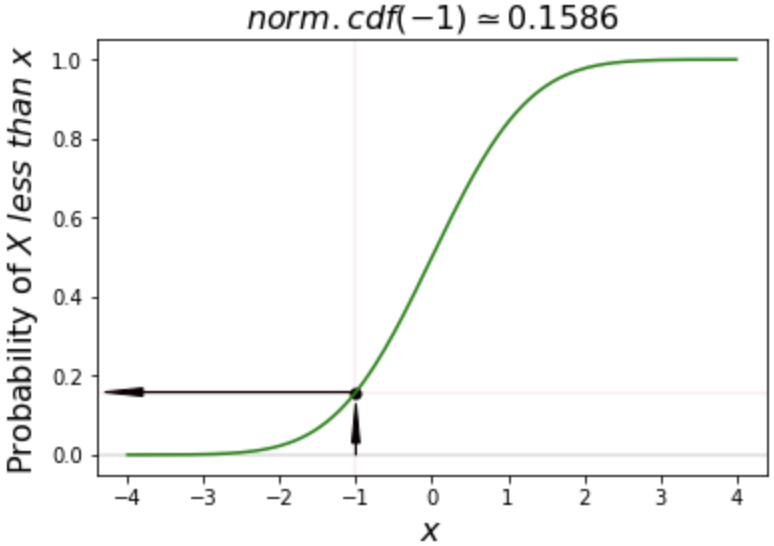
Plot of cumulative distribution function for -1

# Calculate cdf of -1
norm.cdf(-1)

0.15865525393145707

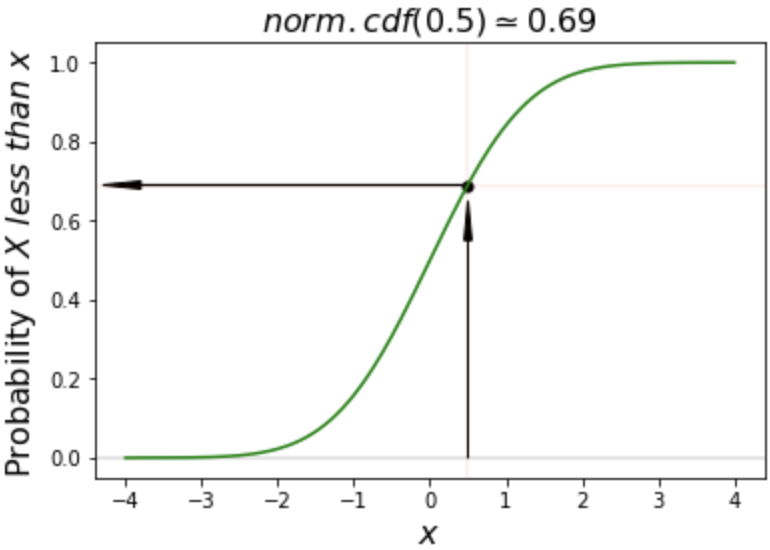
Plot of cumulative distribution function for 0.5

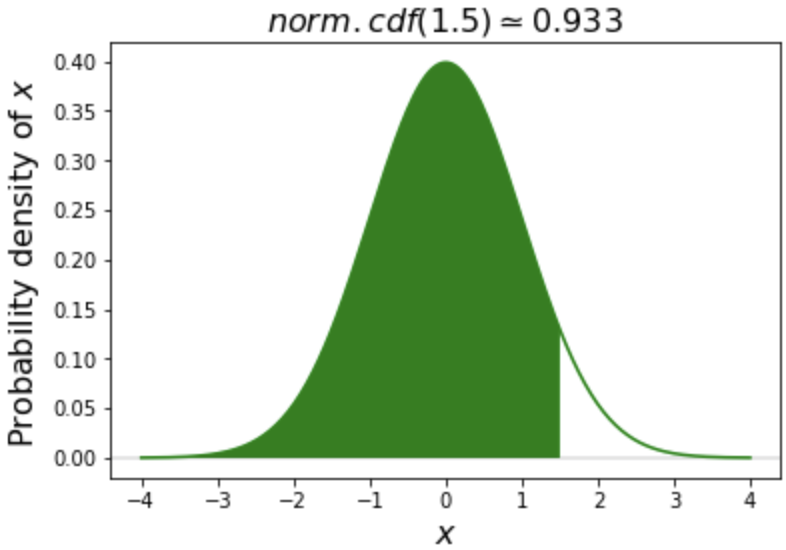
# Calculate cdf of 0.5
norm.cdf(0.5)

0.6914624612740131

Percent point function for 0.2

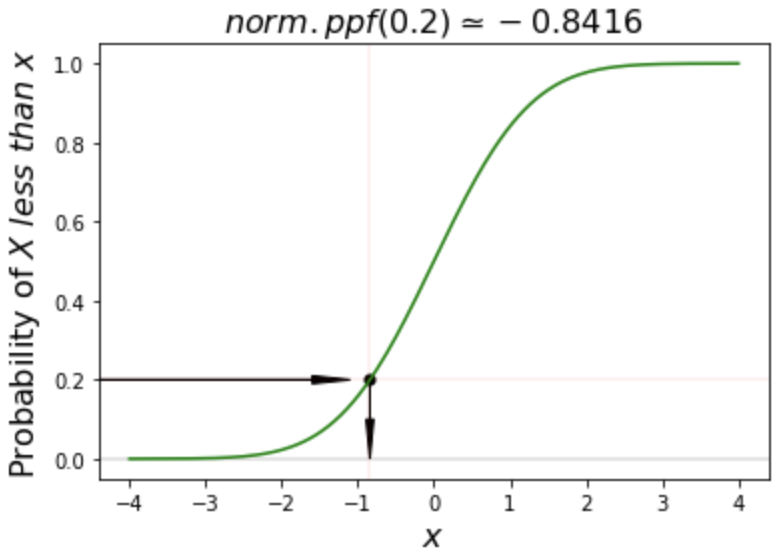
# Calculate ppf of 0.2
norm.ppf(0.2)

-0.8416212335729142

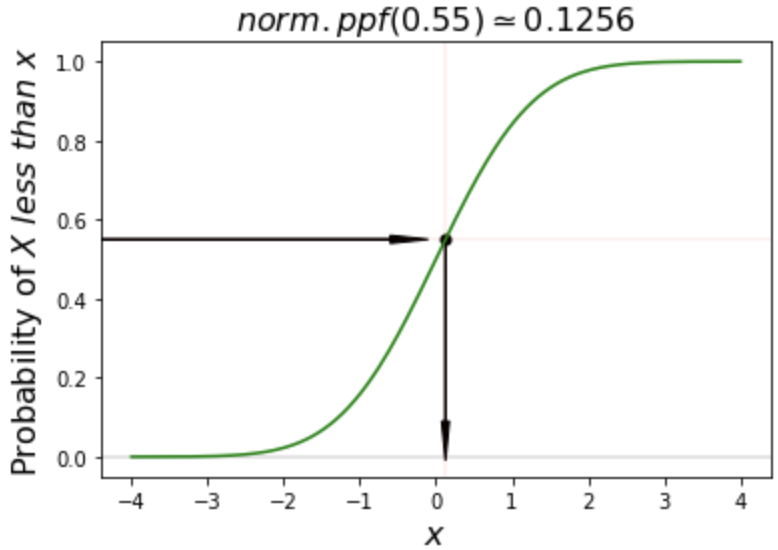
Percent point function for 0.55

# Calculate ppf of 55%
norm.ppf(0.55)

0.12566134685507416

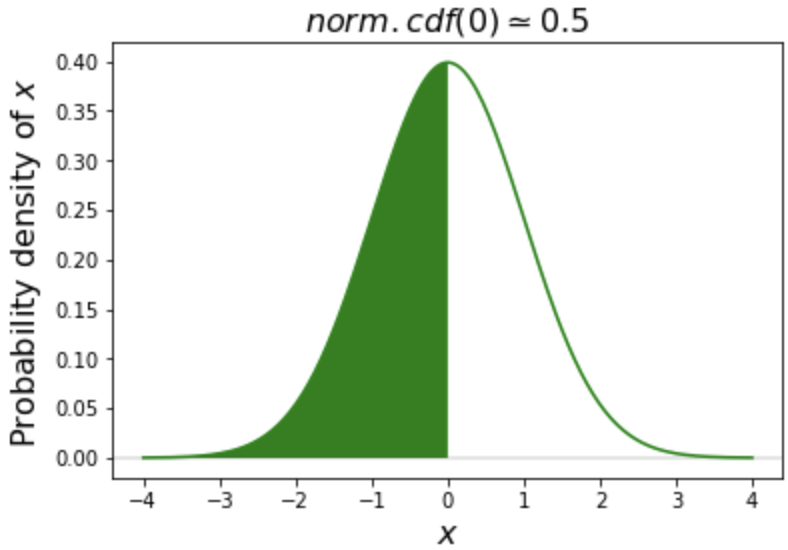
Cumulative distribution function for 0

# Calculate cdf of value 0
norm.cdf(0)

0.5

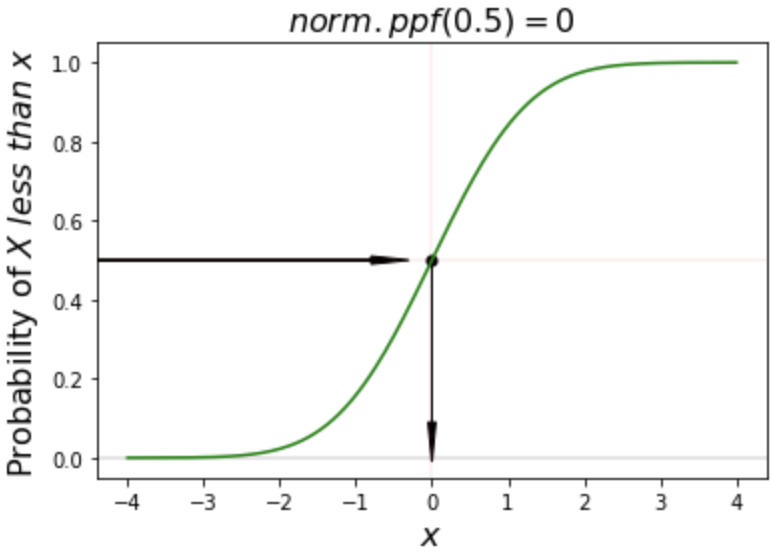
Percent point function for 0.5

# Calculate ppf of probability 50%
norm.ppf(0.5)

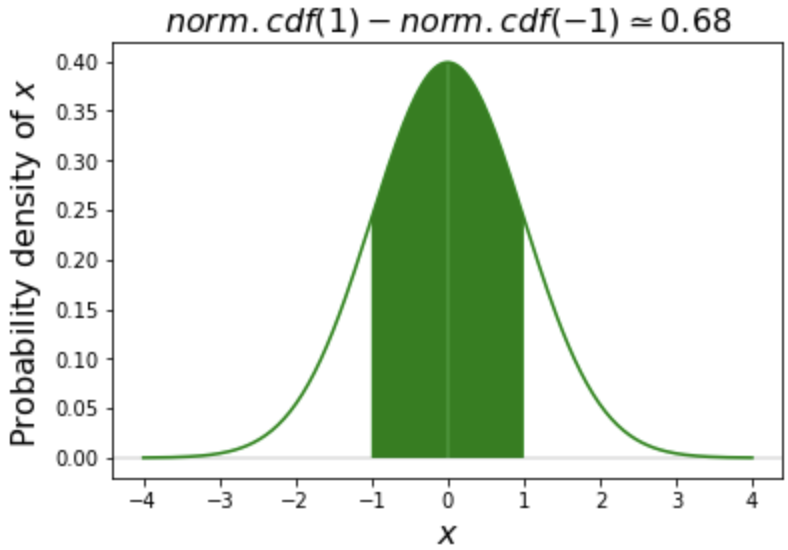
$$ $$ Probability of x less than 1 and greater than -1

$$ $$

# Create our variables
a = -1
b = 1
# Calculate the probability between
# two values, subtracting
norm.cdf(b) - norm.cdf(a)

0.6826894921370859

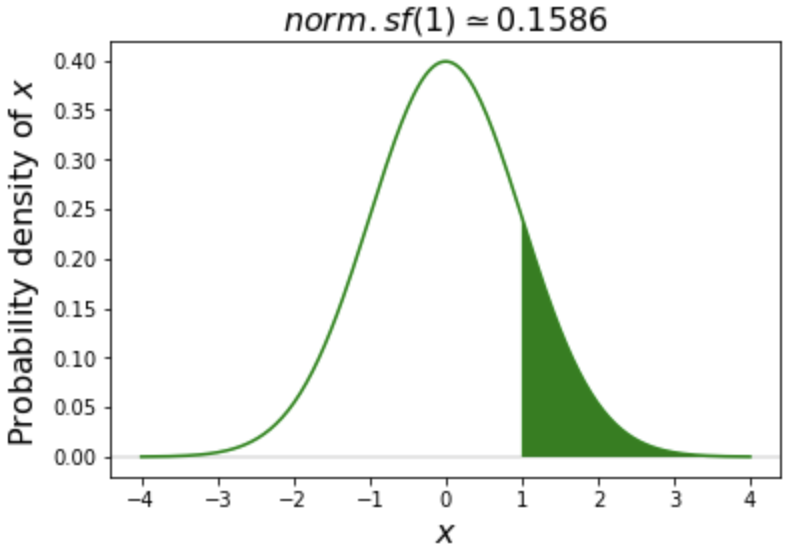
$$ $$ Probability of x greater than 1

$$ $$

# Create our variable
a = 1

# Calculate the complement 
# of cdf() using sf()
norm.sf(a)

0.15865525393145707

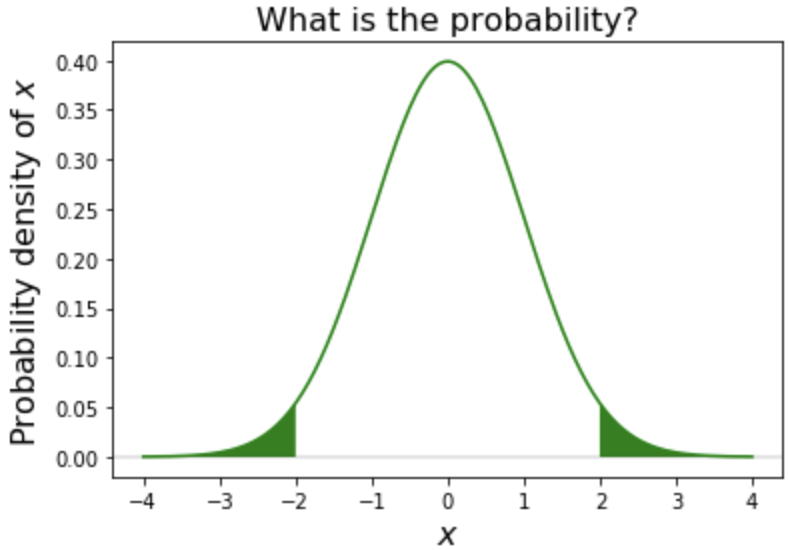
$$ $$ Probability of x greater than 2 and less than -2

$$ $$

# Create our variables
a = -2
b = 2
# Calculate tail probability 
# by adding each tail
norm.cdf(a) + norm.sf(b)

0.04550026389635839

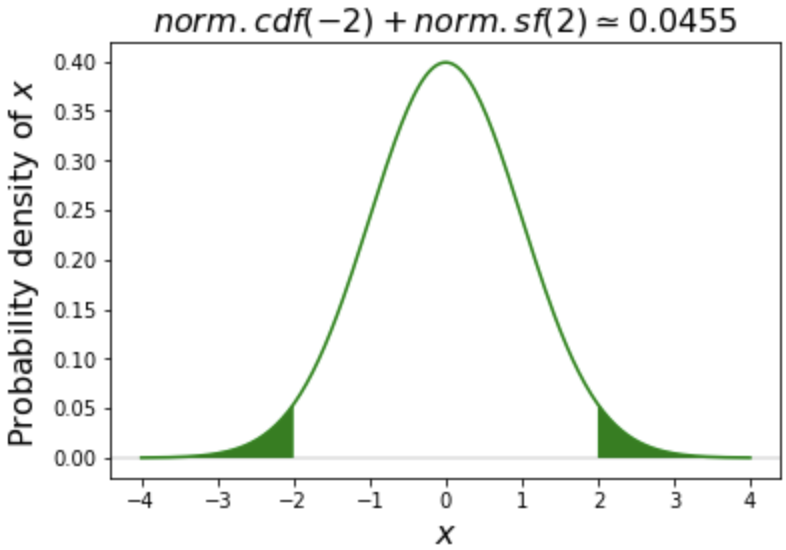
$$ $$ Probability of x greater than 2 and less than -2

$$ $$

# Create our variables
a = -2
b = 2

# Calculate tail probability 
# by adding each tail
norm.cdf(a) + norm.sf(b)

0.04550026389635839

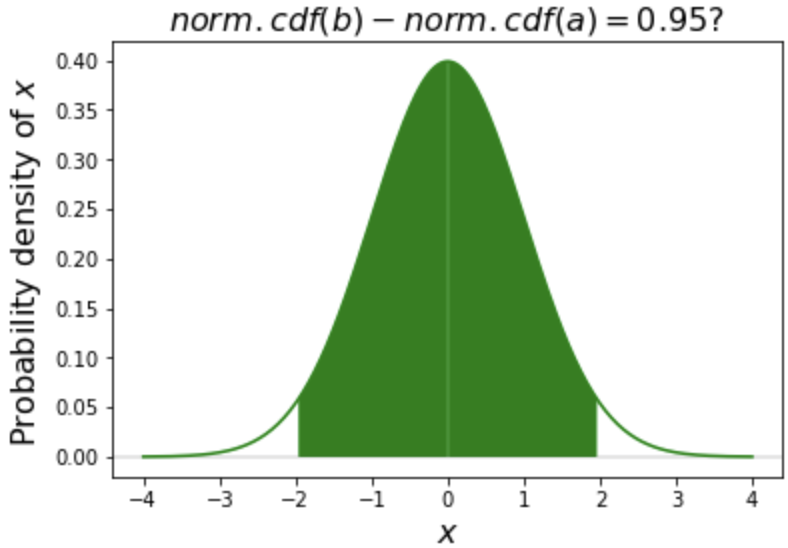
$$ $$ Values of a and b to get 0.95 probability

$$ $$

# Create our variable
alpha = 0.95

# Calculate the interval
norm.interval(alpha)

(-1.959963984540054, 1.959963984540054)

Foundations of Probability in Python