From sample mean to population mean

Foundations of Probability in Python

Alexander A. Ramírez M.

CEO @ Synergy Vision

Sample mean review

$$ $$

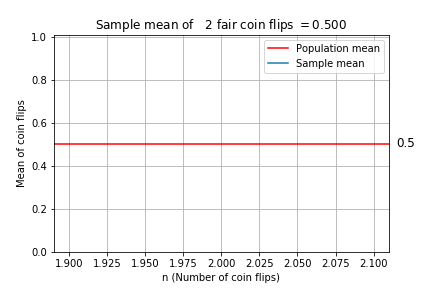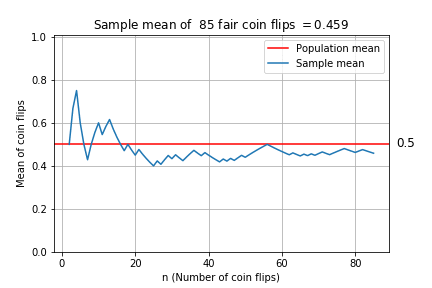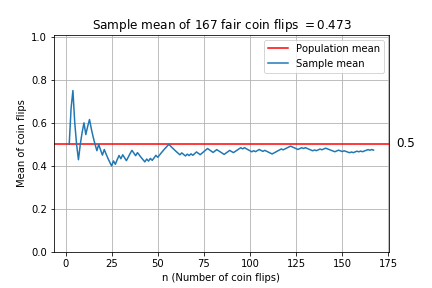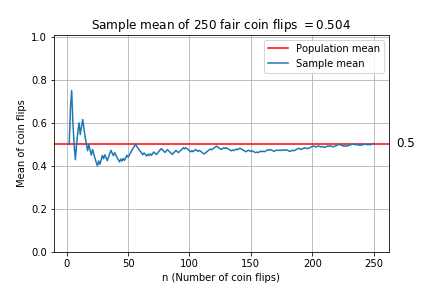
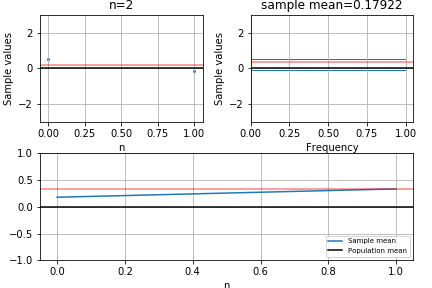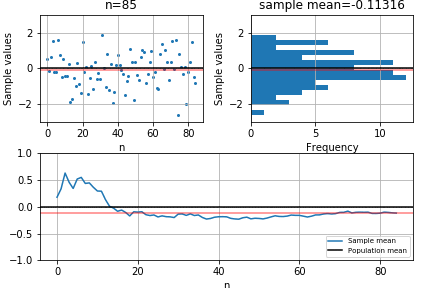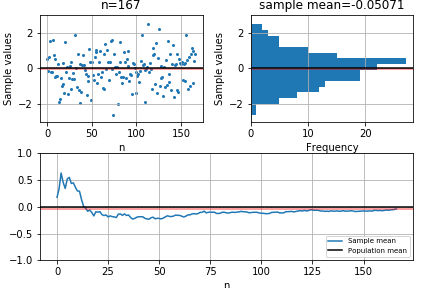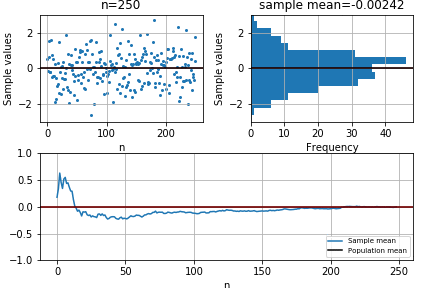
Law of large numbers

The sample mean approaches the expected value as the sample size increases.

Jakob Bernoulli stamp

Sample mean review (Cont.)

$$ \text{Sample mean} = \bar{X_2} = \frac{x_1+x_2}{2} $$

Sample mean review (Cont.)

$$ \text{Sample mean} = \bar{X_3} = \frac{x_1+x_2+x_3}{3} $$

Sample mean review (Cont.)

$$ \text{Sample mean} = \bar{X_n} = \frac{x_1+x_2+\cdots +x_n}{n} $$

Sample mean review (Cont.)

$$ \text{Sample mean} = \bar{X_n} = \frac{x_1+x_2+\cdots +x_n}{n} \to \mathbb{E(X)} $$

Generating the sample

# Import binom and describe
from scipy.stats import binom
from scipy.stats import describe

# Sample of 250 fair coin flips
samples = binom.rvs(n=1, p=0.5, size=250, random_state=42)

# Print first 100 values from the sample
print(samples[0:100])

[0 1 1 1 0 0 0 1 1 1 0 1 1 0 0 0 0 1 0 0 1 0 0 0 0 1 0 1 1 0 1 0 0 1 1 1 0
 0 1 0 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 1 0 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 0 1
 1 1 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 1 0 0 0]

Calculating the sample mean

# Calculate the sample mean
print(describe(samples[0:10]).mean)

0.6

Sample mean convergence to the expected value

Sample mean animation to the expected value

Plotting the sample mean

$$ $$

from scipy.stats import binom
from scipy.stats import describe
import matplotlib.pyplot as plt

# Define our variables
coin_flips, p, sample_size , averages = 1, 0.5, 1000, []

# Generate the sample
samples = binom.rvs(n=coin_flips, p=p, size=sample_size, random_state=42)

Plotting the sample mean (Cont.)

$$ $$

# Calculate the sample mean
for i in range(2,sample_size+1):
    averages.append(describe(samples[0:i]).mean)

# Print the first values of averages
print(averages[0:10])

[0.5, 0.6666666666666666, 0.75, 0.6, 0.5, 0.42857142857142855, 0.5, 
0.5555555555555556,0.6, 0.5454545454545454]

Plotting the sample mean (Cont.)

$$ $$

# Add population mean line and sample mean plot
plt.axhline(binom.mean(n=coin_flips, p=p), color='red')
plt.plot(averages, '-')

# Add legend
plt.legend(("Population mean","Sample mean"), loc='upper right')
plt.show()

Sample mean plot

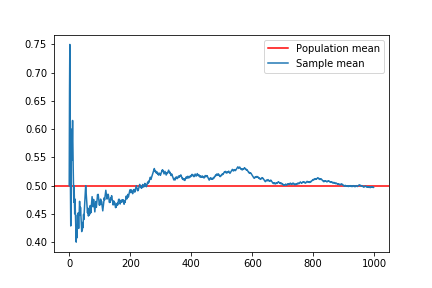
Let's practice!

Foundations of Probability in Python