Conditional probabilities

Foundations of Probability in Python

Alexander A. Ramírez M.

CEO @ Synergy Vision

Dependent events

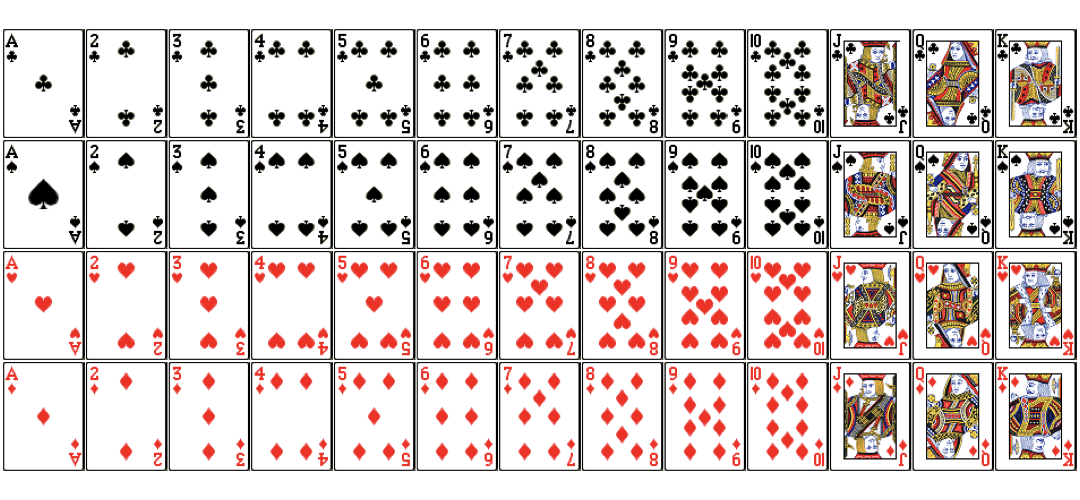
Deck of cards

Dependent events (Cont.)

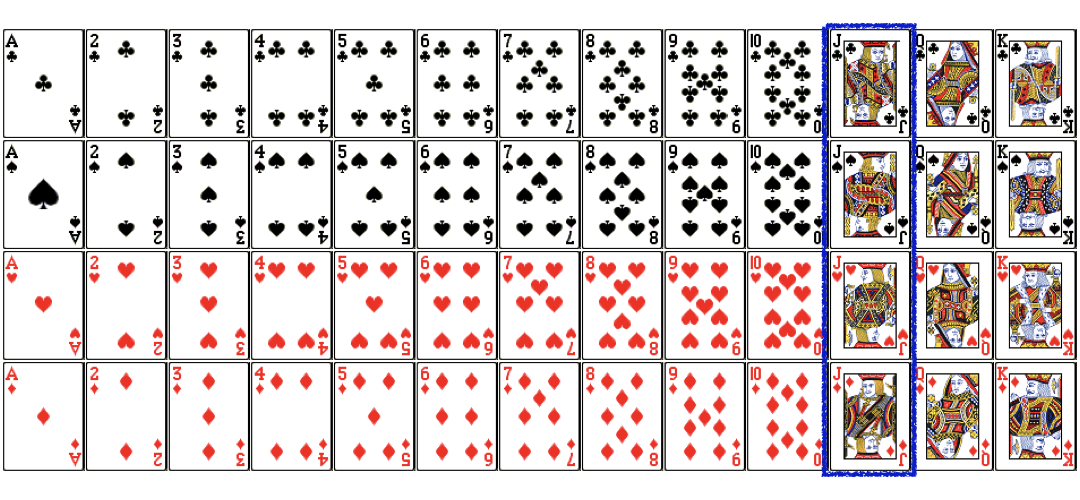
Jacks from a Deck of cards

$$P(Jack) = \frac{4}{52} \simeq 7.69\%$$

Dependent events (Cont.)

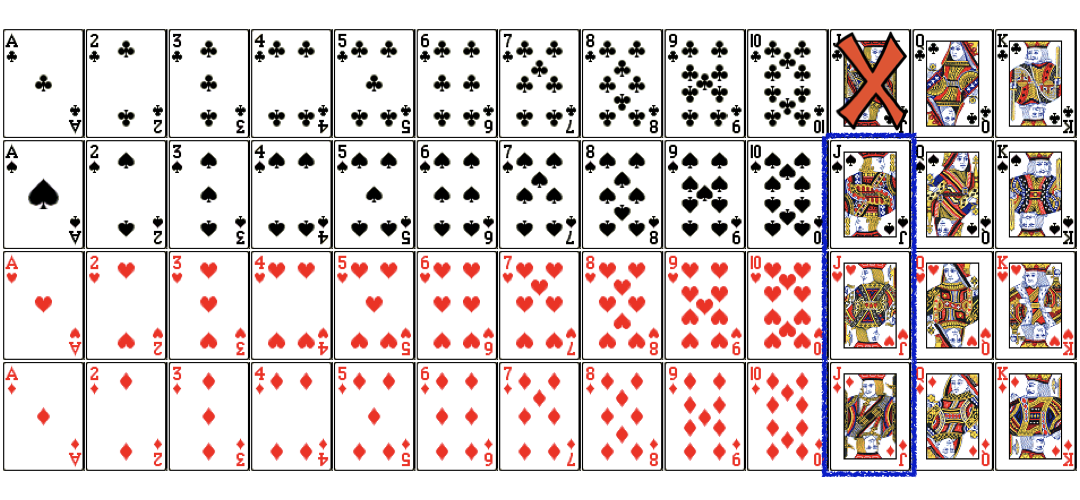
Three Jacks from a Deck of cards

$$P(Jack) = \frac{3}{51} \simeq 5.88\%$$

Conditional probability formula

$$ $$

$$P(A\ and\ B)=P(A)P(B)$$

Conditional probability formula (Cont.)

$$ $$

$$P(A\ and\ B)=P(A)\color{red}{P(B|A)}$$

$$ $$

$$\color{red}{P(B|A)}=\frac{P(A\ and\ B)}{P(A)}$$

Conditional probability

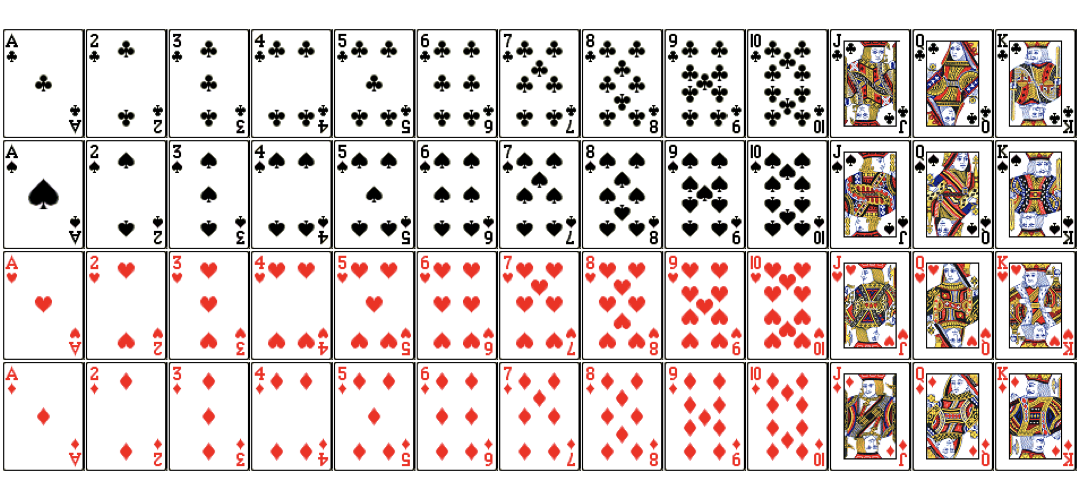
Deck of cards

Conditional probability (Cont.)

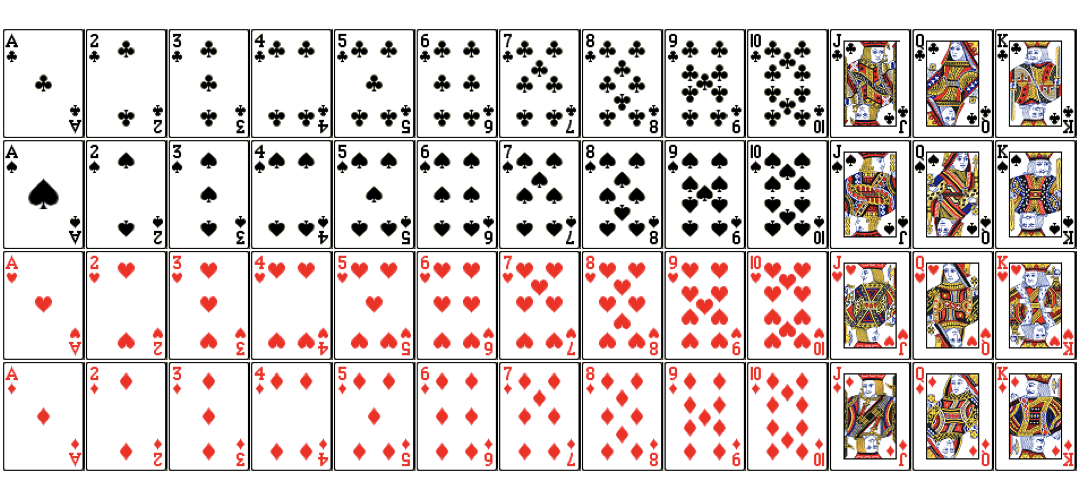
Deck of cards

$$P(Red|Jack)=?$$

Conditional probability (Cont.)

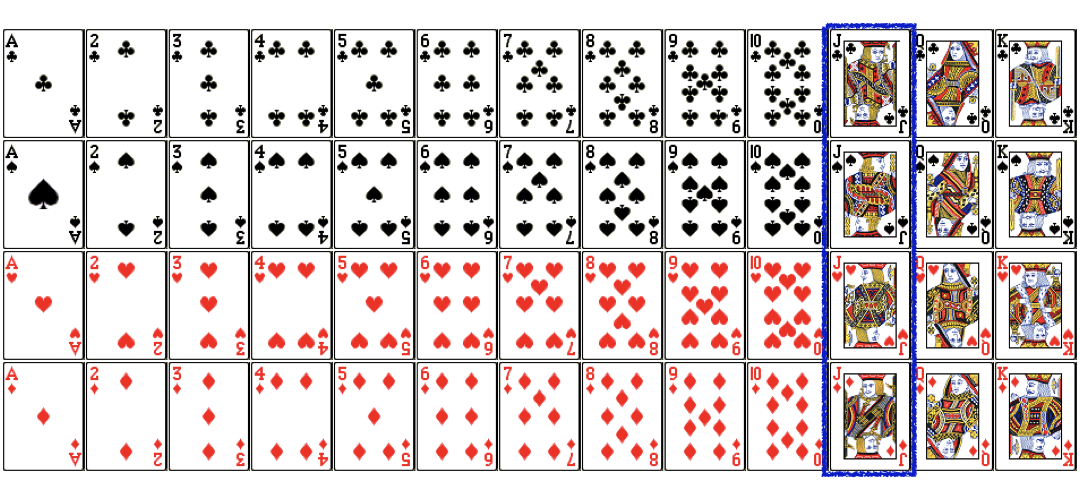
Jacks from a Deck of cards

$$P(Red|Jack) = \frac{P(Jack\ and\ Red)}{P(Jack)}$$

Conditional probability (Cont.)

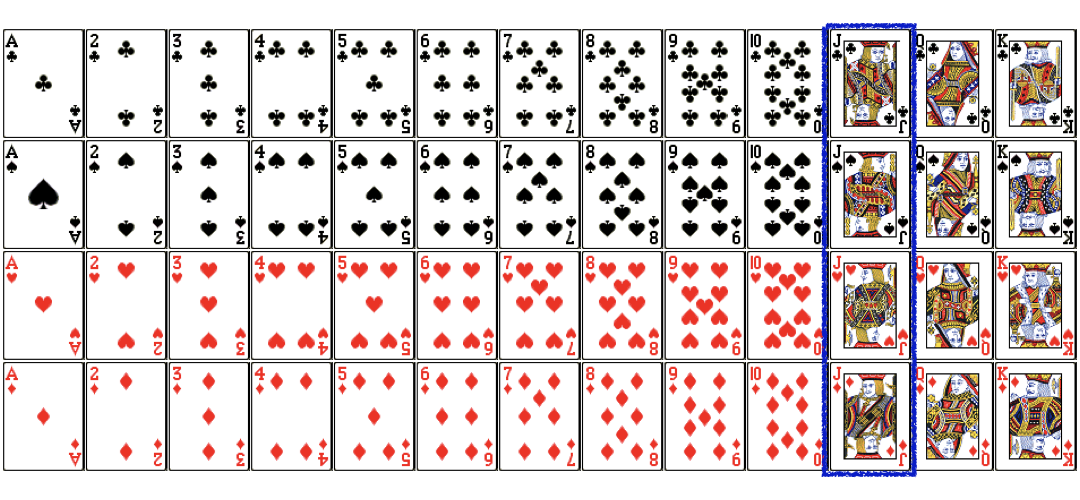
Jacks from a Deck of cards

$$P(Red|Jack) = \frac{P(Jack\ and\ Red)}{\color{blue}{P(Jack)}}$$

Conditional probability (Cont.)

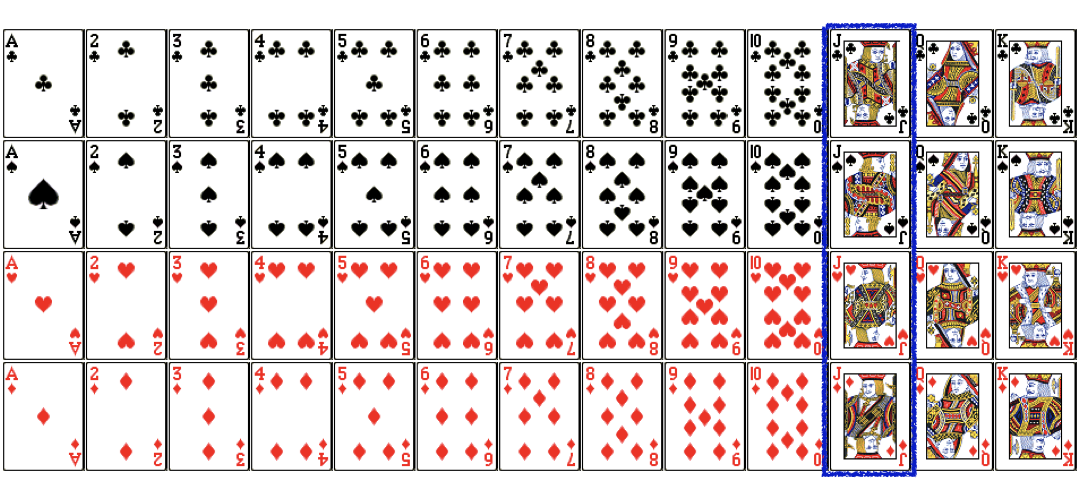Jacks from a Deck of cards $$P(Red|Jack) = \frac{P(Jack\ and\ Red)}{\color{blue}{P(Jack)}} = \frac{X}{\color{blue}{\frac{4}{52}}}$$

Conditional probability (Cont.)

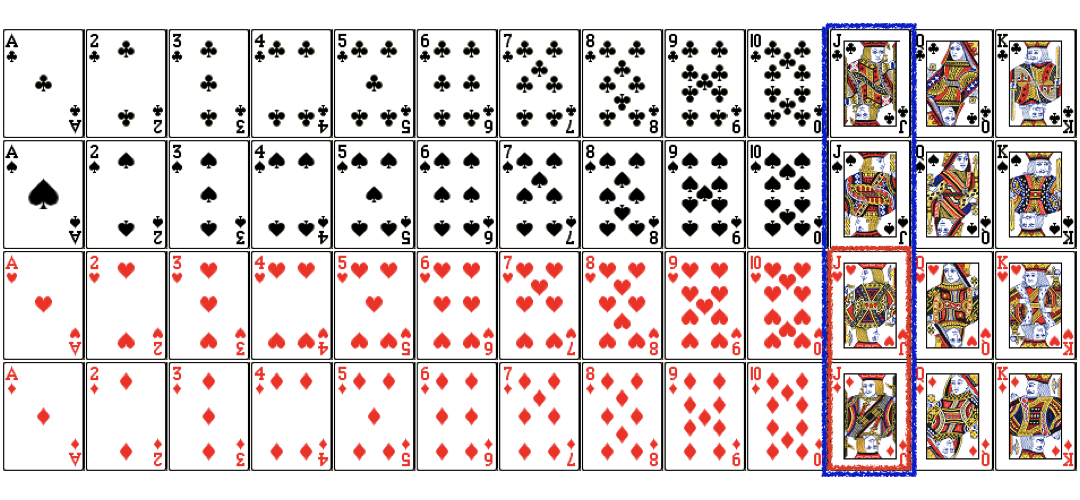
Red Jacks from a Deck of cards

$$P(Red|Jack) = \frac{\color{red}{P(Jack\ and\ Red)}}{P(Jack)} = \frac{\color{red}{\frac{2}{52}}}{\frac{4}{52}}$$

Conditional probability (Cont.)

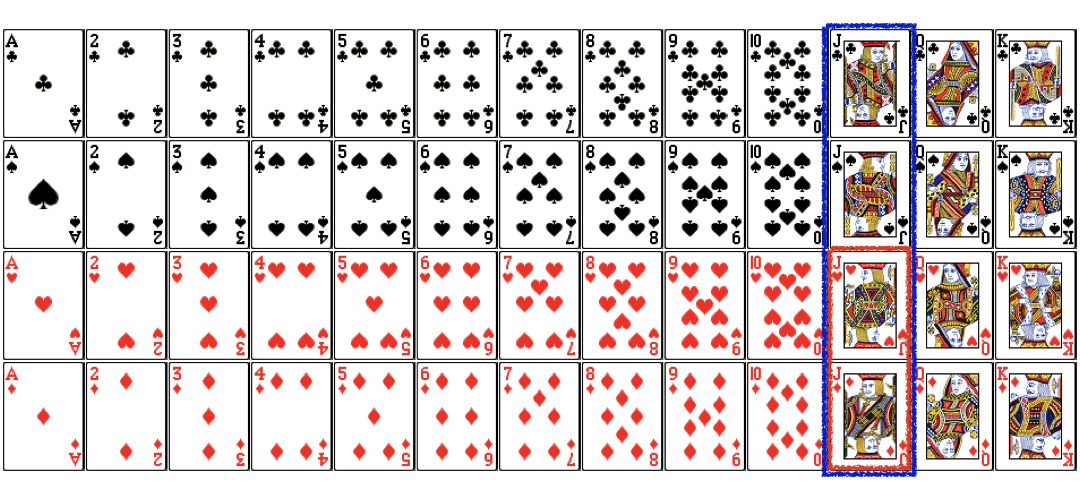
Red Jacks from a Deck of cards

$$P(Red|Jack) = \frac{P(Jack\ and\ Red)}{P(Jack)} = \frac{\frac{2}{52}}{\frac{4}{52}} = \frac{2}{4} = \frac{1}{2}$$

Conditional probability (Cont.)

Red Jacks over Total Jacks from a Deck of Cards

$$P(Red|Jack) = \frac{P(Jack\ and\ Red)}{P(Jack)} = \frac{\frac{2}{52}}{\frac{4}{52}} = \frac{2}{4} = \frac{1}{2}$$

P(Red | Jack) calculation in Python

P_Jack = 4/52
P_Jack_n_Red = 2/52

P_Red_given_Jack = P_Jack_n_Red / P_Jack

print(P_Red_given_Jack)

0.5

Conditional probability

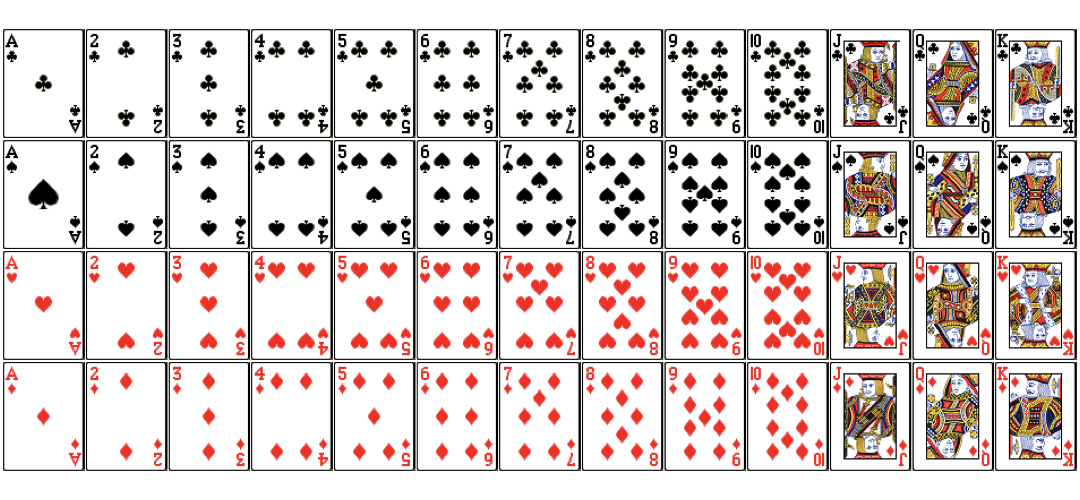
Deck of cards

$$P(Jack|Red)=?$$

Conditional probability (Cont.)

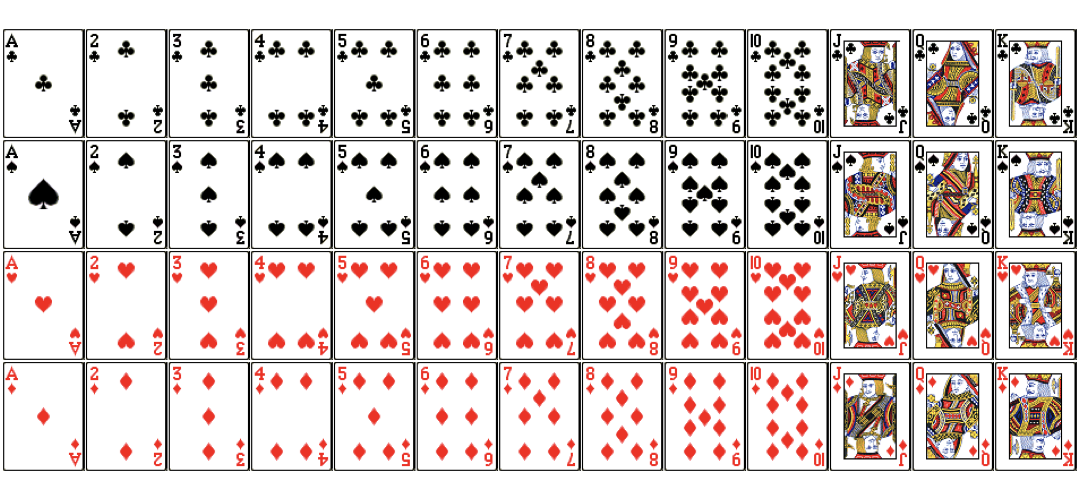
Deck of cards

$$P(Jack|Red)=\frac{P(Red\ and\ Jack)}{P(Red)}$$

Conditional probability (Cont.)

Red cards from a Deck of cards

$$P(Jack|Red) = \frac{P(Red\ and\ Jack)}{P(Red)}$$

Conditional probability (Cont.)

Red cards from a Deck of cards

$$P(Jack|Red) = \frac{P(Red\ and\ Jack)}{\color{red}{P(Red)}}$$

Conditional probability (Cont.)

Red cards from a Deck of cards

$$P(Jack|Red) = \frac{P(Red\ and\ Jack)}{\color{red}{P(Red)}} = \frac{X}{\color{red}{\frac{26}{52}}}$$

Conditional probability (Cont.)

Red jacks from a Deck of cards

$$P(Jack|Red) = \frac{\color{blue}{P(Red\ and\ Jack)}}{P(Red)} = \frac{\color{blue}{\frac{2}{52}}}{\frac{26}{52}}$$

Conditional probability (Cont.)

Red jacks from a deck of cards

$$P(Jack|Red) = \frac{P(Red\ and\ Jack)}{P(Red)} = \frac{\frac{2}{52}}{\frac{26}{52}} = \frac{2}{26} = \frac{1}{13}$$

Conditional probability (Cont.)

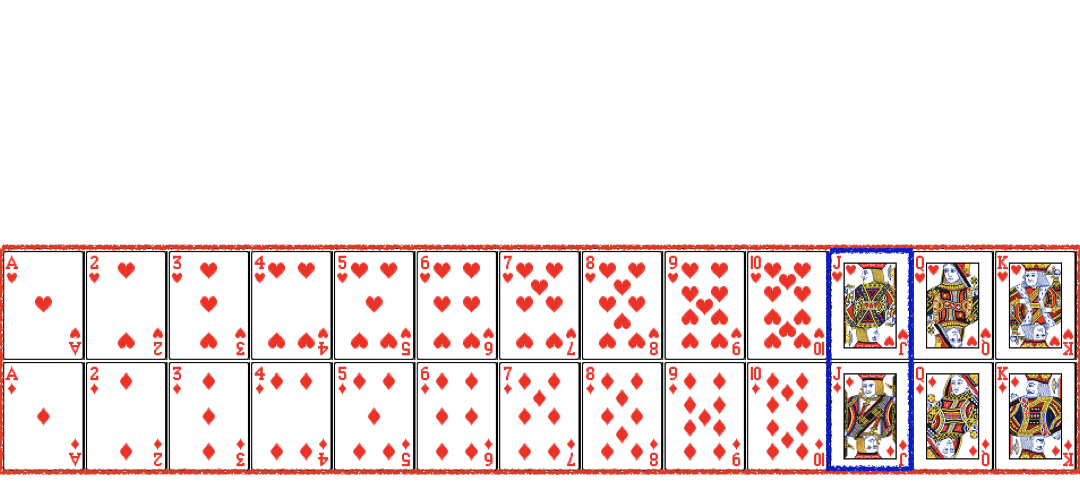
Red jacks from a deck of cards

$$P(Jack|Red) = \frac{P(Red\ and\ Jack)}{P(Red)} = \frac{\frac{2}{52}}{\frac{26}{52}} = \frac{2}{26} = \frac{1}{13}$$

P(Jack | Red) calculation in Python

P_Red = 26/52
P_Red_n_Jack = 2/52

P_Jack_given_Red = P_Red_n_Jack / P_Red

print(P_of_Jack_given_Red)

0.0769230769231

Let's condition events to calculate probabilities

Foundations of Probability in Python