Foundations of Probability in Python
Alexander A. Ramírez M.
CEO @ Synergy Vision
Expected value: sum of possible outcomes weighted by it's probability.
$$ E(X) = \sum_{i=1}^{k} x_ip_i = x_1p_1 + x_2p_2 + \cdots + x_kp_k $$
The expected value of a discrete random variable is the sum of the possible outcomes weighted by their probability.
In our case, for the coin flip we get:
$$ E(X) = \sum_{i=1}^{2} x_ip_i = x_1p_1 + x_2p_2 = \color{red}{0\times (1-p)} + 1\times p = p $$
$$ E(X) = \sum_{i=1}^{2} x_ip_i = x_1p_1 + x_2p_2 = 0\times (1-p) + \color{red}{1\times p} = p $$
Each $x_i$ is the outcome from one experiment (i.e., a coin flip, either 0 or 1).
$$ \bar{X} = \frac{1}{n}\sum_{i=1}^{n} x_i = \frac{1}{n}(x_1+x_2+\cdots +x_n) $$
In Python we will use the scipy.stats.describe() function to get the arithmetic mean.
scipy.stats.describe()
from scipy.stats import describe describe([0,1]).mean
0.5
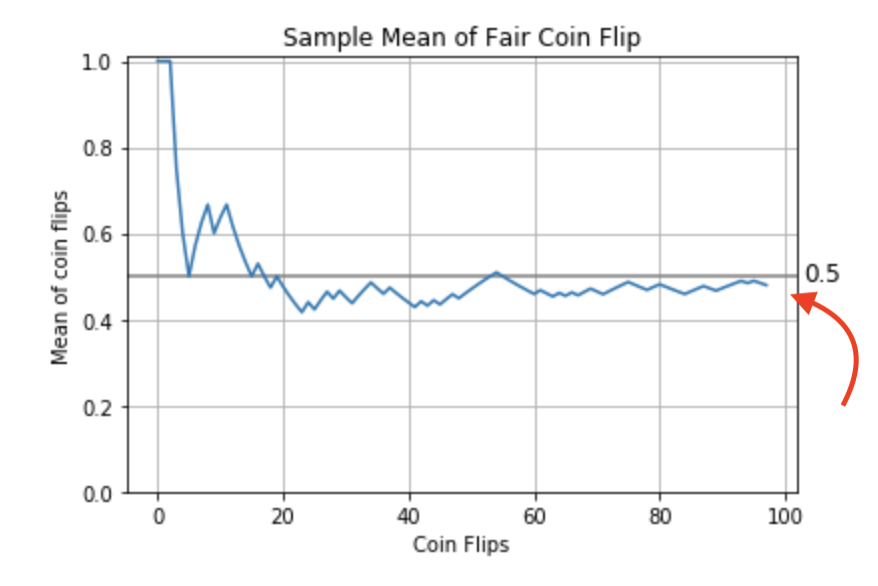
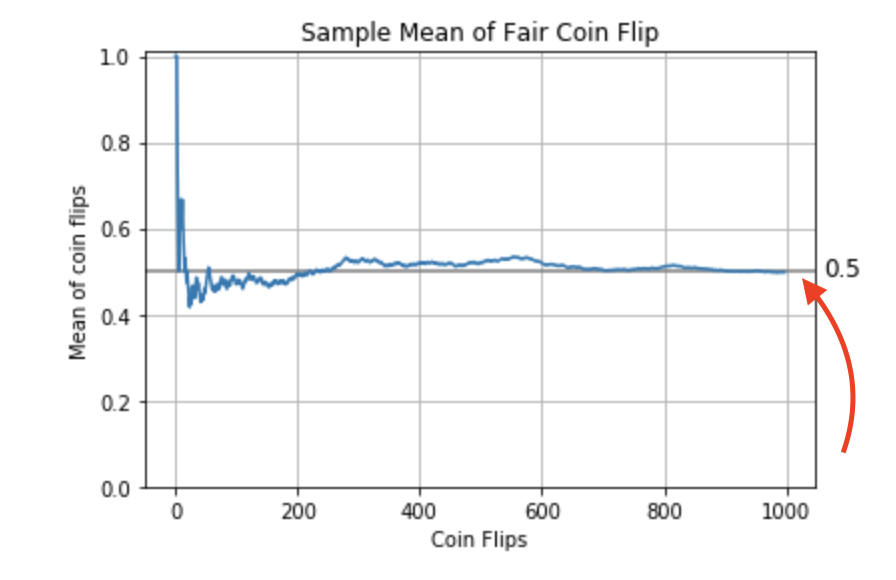
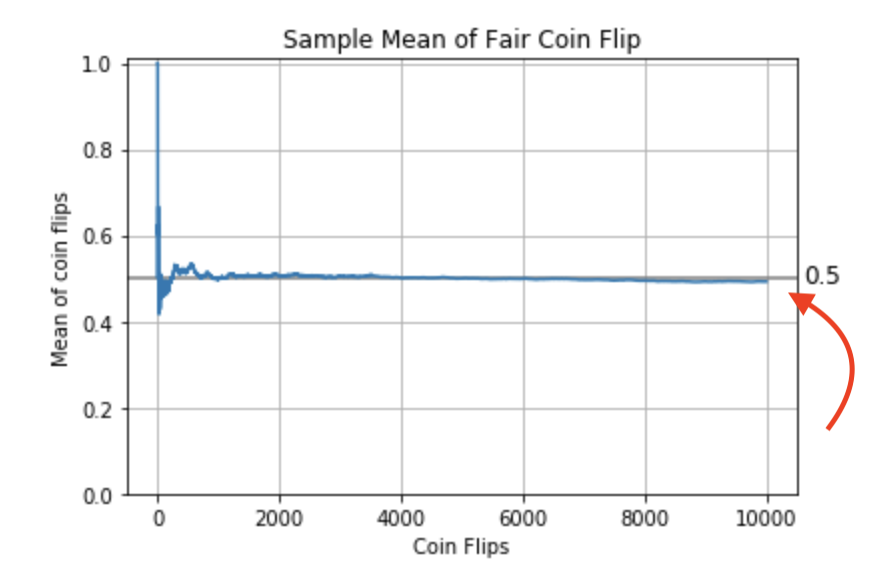
Variance is a measure of dispersion.
It's the expected value of the squared deviation from its expected value.
$$ Var(X) = E[(X - E(X))^2] = \sum_{i=1}^{n}p_i \times (x_i-E(X))^2 $$
In Python, we will use the scipy.stats.describe() function to get the sample variance.
describe([0,1]).variance
For $X\sim Binomial(n, p)$
$$ E(X) = n \times p $$
$$ Var(X) = n \times p \times (1-p) $$
Example: $n=10$ and $p=0.5$
In Python we will use the binom.stats() method to get the expected value and variance.
binom.stats()
binom.stats(n=10, p=0.5)
(array(5.), array(2.5))
What are the expected value and variance for one fair coin flip?
binom.stats(n=1, p=0.5)
(array(0.5), array(0.25))
What are the expected value and variance for one biased coin flip, with 30% probability of success?
binom.stats(n=1, p=0.3)
(array(0.3), array(0.21))
What are the expected value and variance for 10 fair coin flips?
Preparing Video For Download...
