Calculating probabilities of two events

Foundations of Probability in Python

Alexander A. Ramírez M.

CEO @ Synergy Vision

Independence

Given that A and B are events in a random experiment, the conditions for independence of A and B are:

1. The order in which A and B occur does not affect their probabilities.
2. If A occurs, this does not affect the probability of B.
3. If B occurs, this does not affect the probability of A.

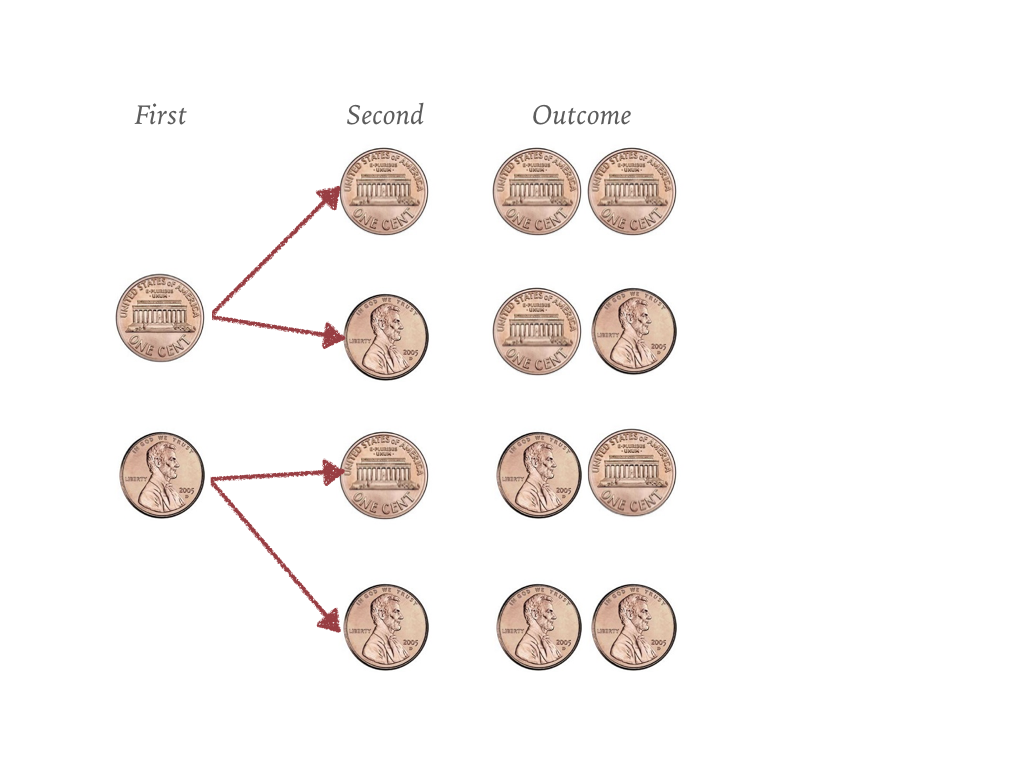
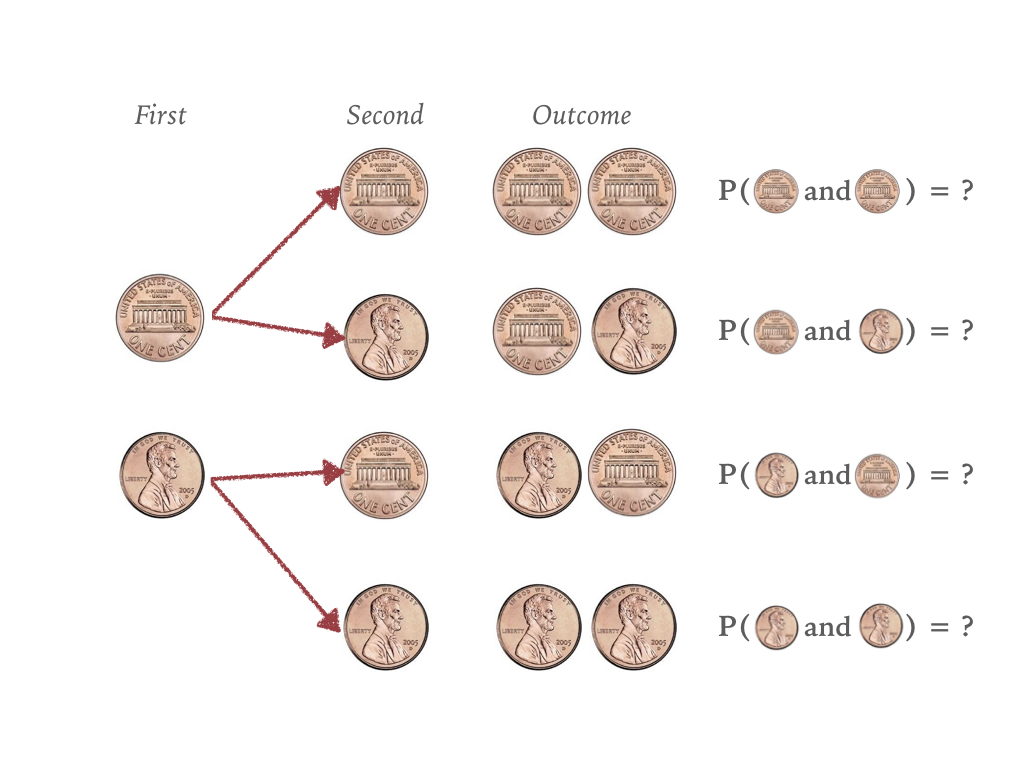
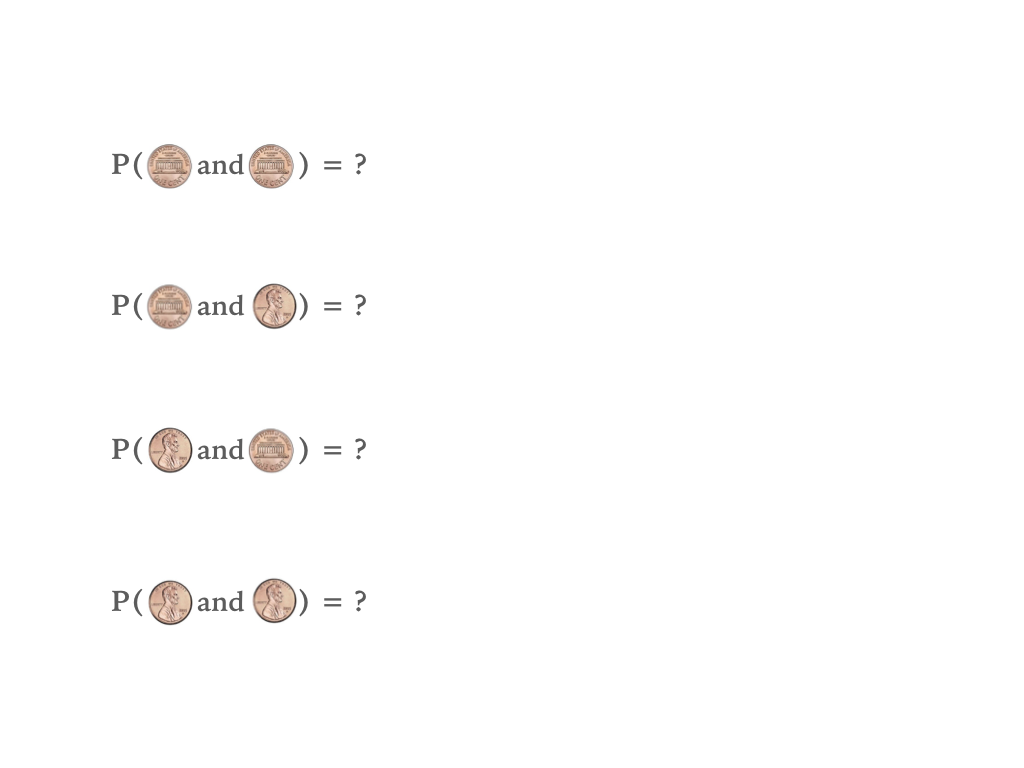
Measuring a sample

Generate a sample that represents 1000 throws of two fair coin flips

from scipy.stats import binom
sample = binom.rvs(n=2, p=0.5, size=1000, random_state=1)

array([1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 2, 0, 1, 1, 1, 0, 0, 2, 2,...

Find repeated data

from scipy.stats import find_repeats
find_repeats(sample)

RepeatedResults(values=array([0., 1., 2.]), counts=array([249, 497, 254]))

Measuring a biased sample

Using biased_sample data generated, calculate the relative frequency of each outcome

from scipy.stats import relfreq
relfreq(biased_sample, numbins=3).frequency

array([0.039, 0.317, 0.644])

Joint probability calculation

$$ $$

	Engine	Gear box
Fails	0.01	0.005
Works	0.99	0.995

$$ $$ $$P(Engine\ fails\ and\ Gear\ box\ fails)=?$$

$$ $$

P_Eng_fail = 0.01
P_GearB_fail = 0.005
P_both_fails = P_Eng_fail*P_GearB_fail
print(P_both_fails)

0.00005

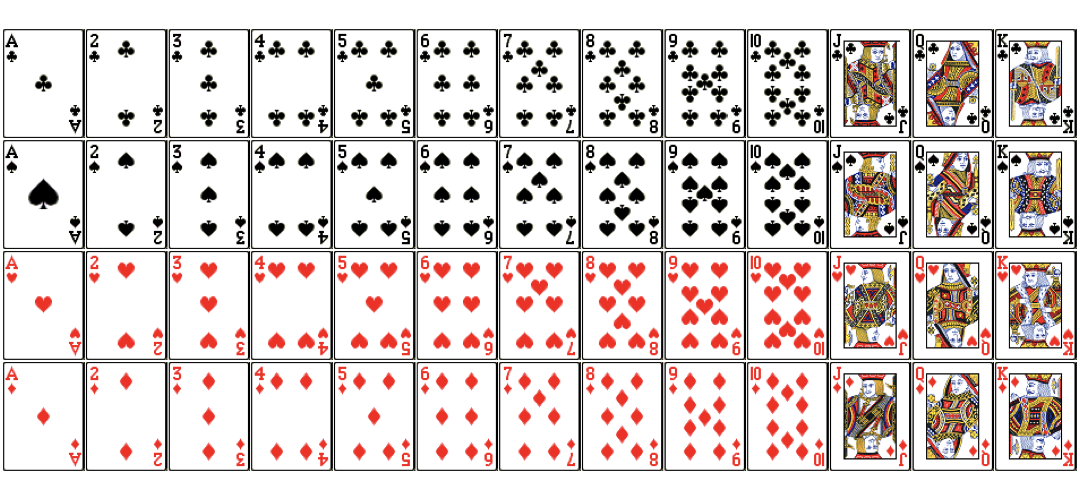
P(A or B) with cards

$$P(Jack\ or\ King) = ?$$

P(A or B) with cards (Cont.)

$$P(Jack\ or\ King) = \color{red}{P(Jack)}+...$$ 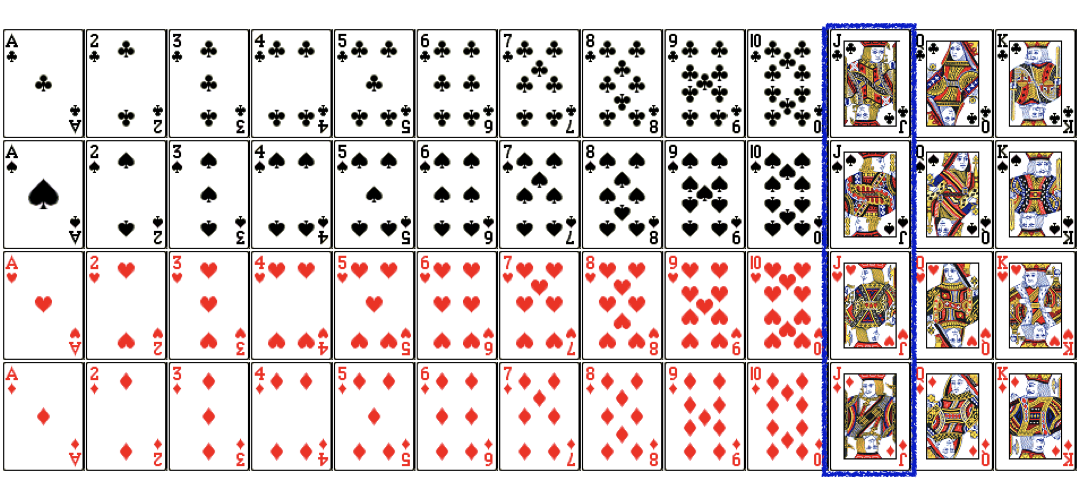$$P(Jack\ or\ King) = \color{red}{\frac{4}{52}}+...$$

P(A or B) with cards (Cont.)

$$P(Jack\ or\ King) = P(Jack)+\color{red}{P(King)}$$ 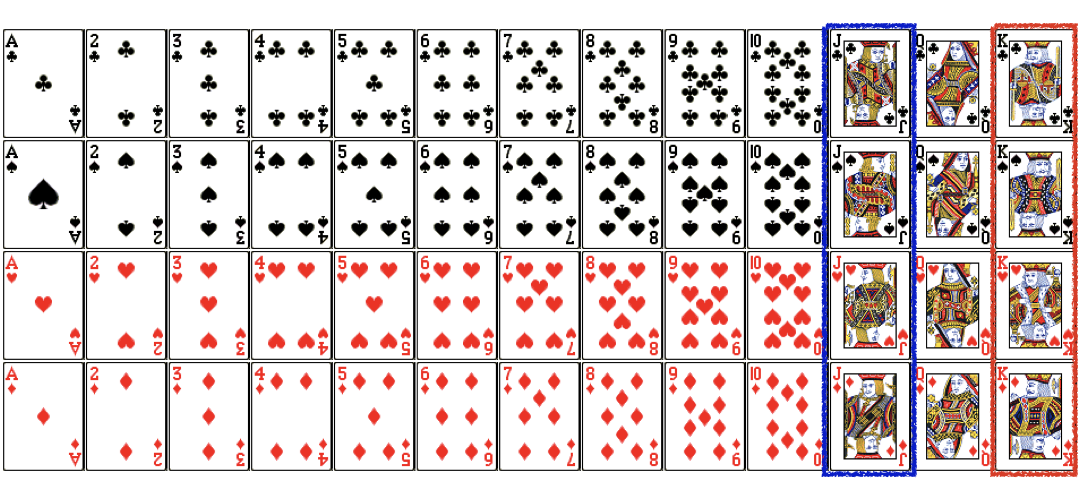$$P(Jack\ or\ King) = \frac{4}{52}+\color{red}{\frac{4}{52}}$$

P(A or B) with cards (Cont.)

$$P(Jack\ or\ King) = P(Jack)+P(King)$$ 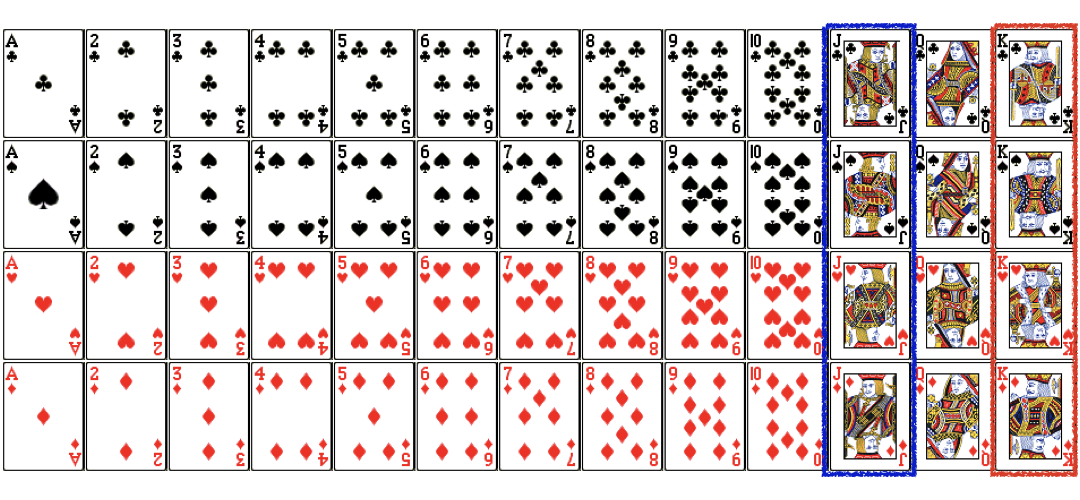$$P(Jack\ or\ King) = \frac{4}{52}+\frac{4}{52}=\frac{8}{52}=\frac{2}{13}$$

P(A or B) with cards (Cont.)

$$P(Jack\ or\ King) = P(Jack)+P(King)$$ $$P(Jack\ or\ King) = \frac{4}{52}+\frac{4}{52}=\frac{8}{52}=\frac{2}{13}$$

Probability of A or B

Probability of A or B (Cont.)

Probability of A or B (Cont.)

$$P(A\ or\ B) = ?$$

Probability of A or B (Cont.)

$$P(A\ or\ B) = \color{red}{P(A)}+...$$

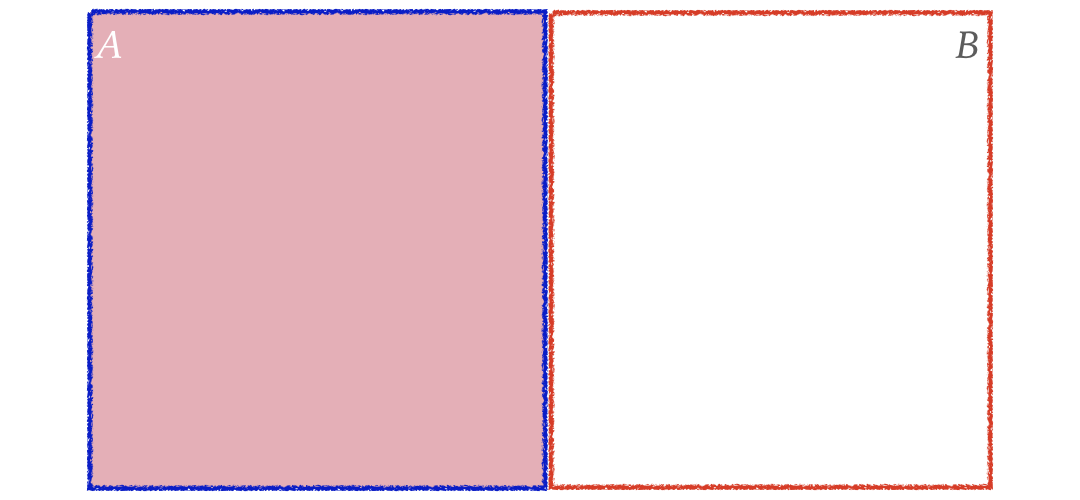
Probability of A or B (Cont.)

$$P(A\ or\ B) = P(A) + \color{red}{P(B)}$$

P(A or B) with overlap

$$P(Jack\ or\ Heart)=?$$

P(A or B) with overlap (Cont.)

$$P(Jack\ or\ Heart) =\color{red}{P(Jack)}+...$$ 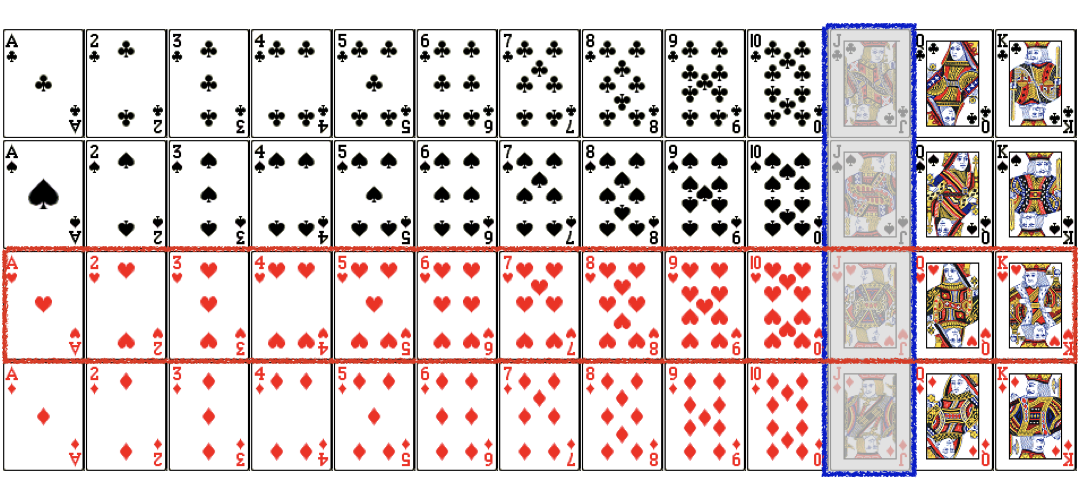$$P(Jack\ or\ Heart) =\color{red}{\frac{4}{52}}+...$$

P(A or B) with overlap (Cont.)

$$P(Jack\ or\ Heart) =P(Jack)+\color{red}{P(Heart)}\ ...$$ 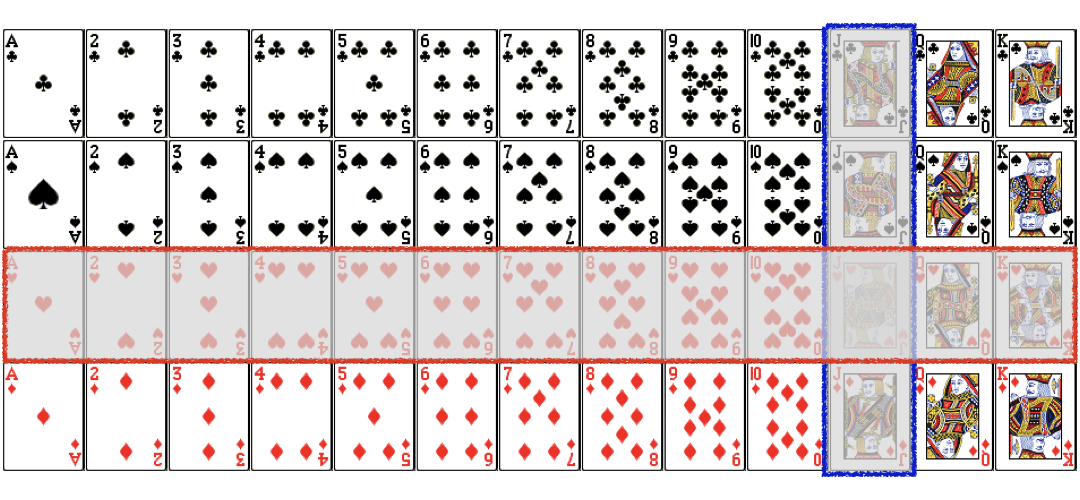$$P(Jack\ or\ Heart) =\frac{4}{52}+\color{red}{\frac{13}{52}}\ ...$$

P(A or B) with overlap (Cont.)

$$P(Jack\ or\ Heart) =P(Jack)+P(Heart)...$$ 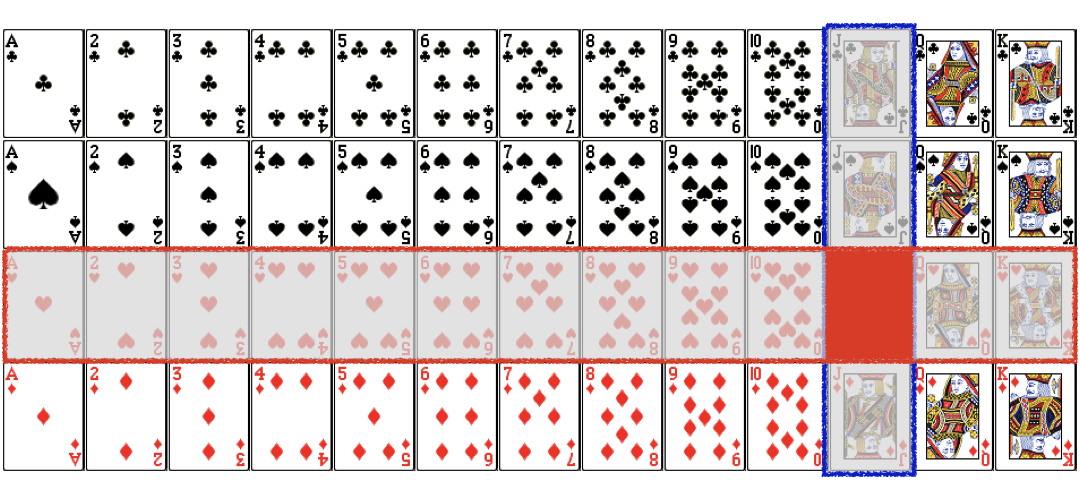$$P(Jack\ or\ Heart) =\frac{4}{52}+\frac{13}{52}...$$

P(A or B) with overlap (Cont.)

$$P(Jack\ or\ Heart) =P(Jack)+P(Heart)-\color{red}{P(Jack\ and\ Heart)}$$ 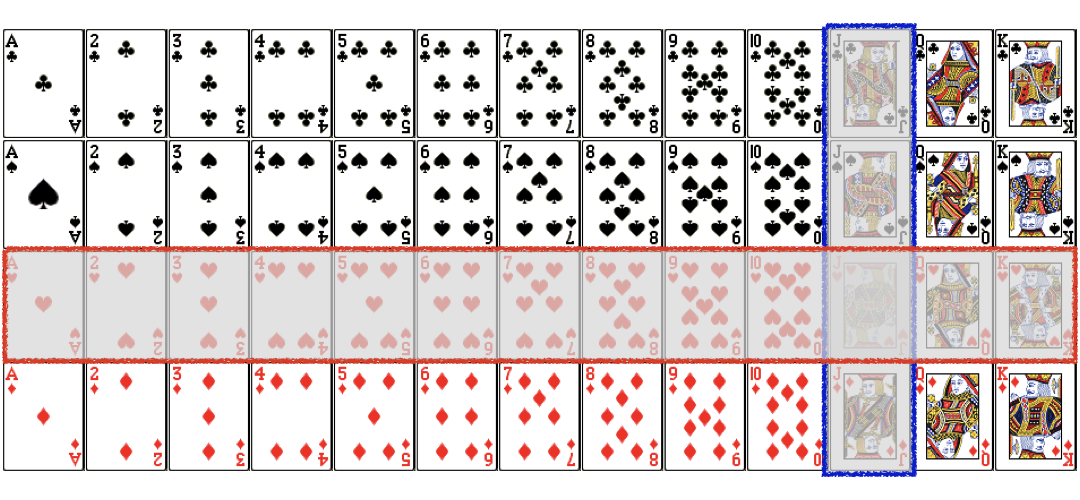$$P(Jack\ or\ Heart) =\frac{4}{52}+\frac{13}{52}-\color{red}{\frac{1}{52}}$$

P(A or B) with overlap (Cont.)

$$P(Jack\ or\ Heart) =P(Jack)+P(Heart)-P(Jack\ and\ Heart)$$ 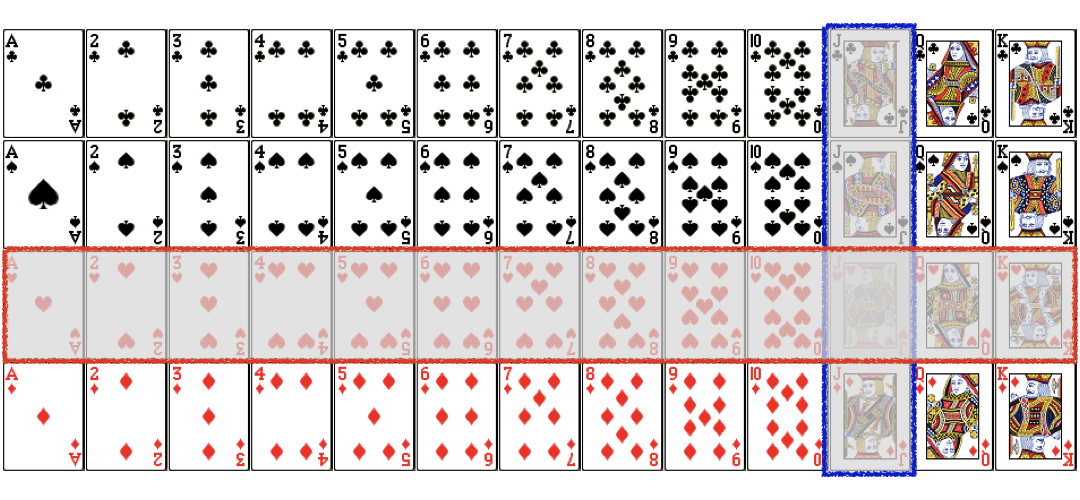$$P(Jack\ or\ Heart) =\frac{4}{52}+\frac{13}{52}-\frac{1}{52}=\frac{16}{52}=\frac{4}{13}$$

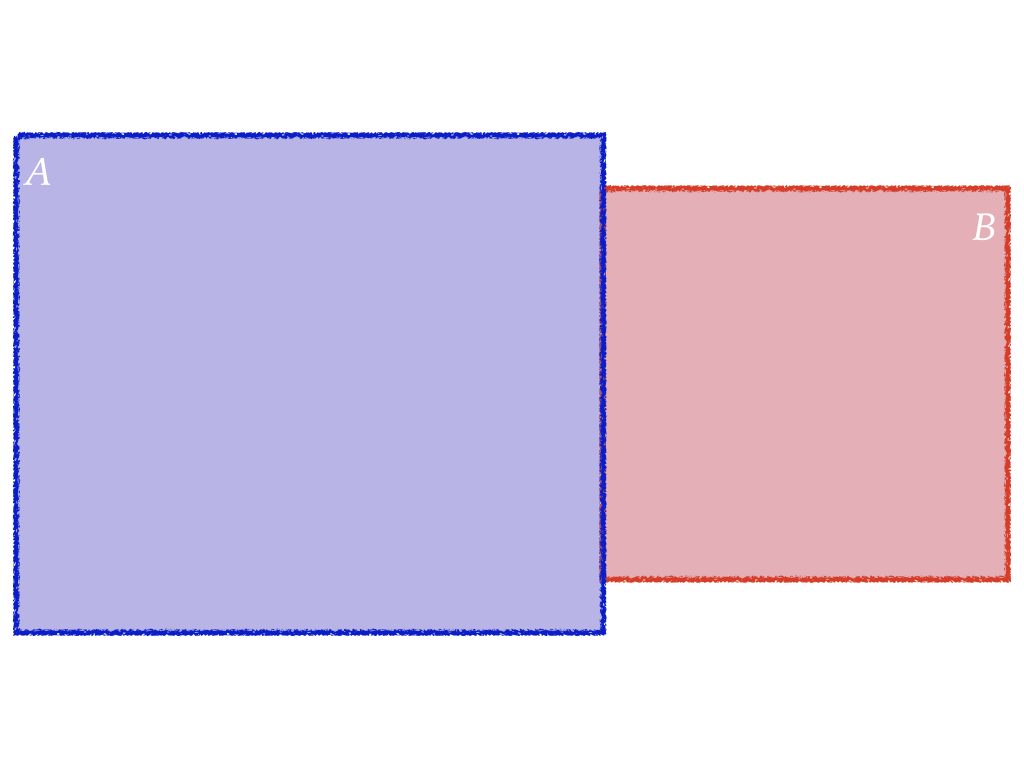
Diagram of P(A or B)

Diagram of P(A or B) (Cont.)

Diagram of P(A or B) (Cont.)

$$P(A\ or\ B)=?$$

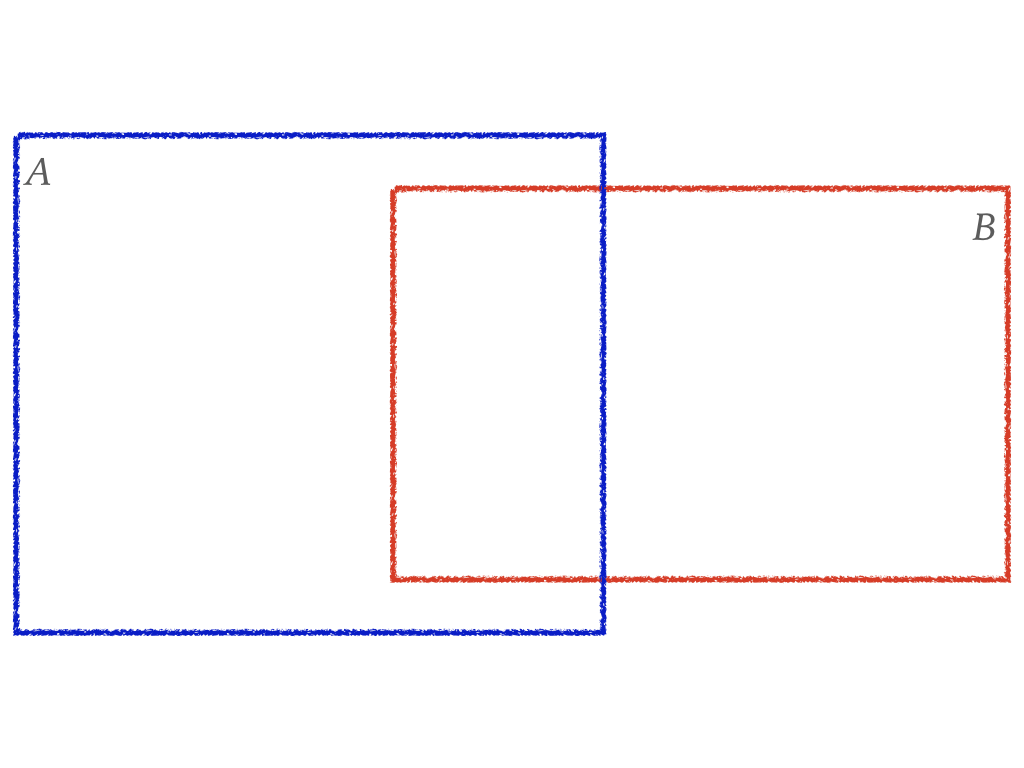
Diagram of P(A or B) (Cont.)

$$P(A\ or\ B)=\color{red}{P(A)}+...$$

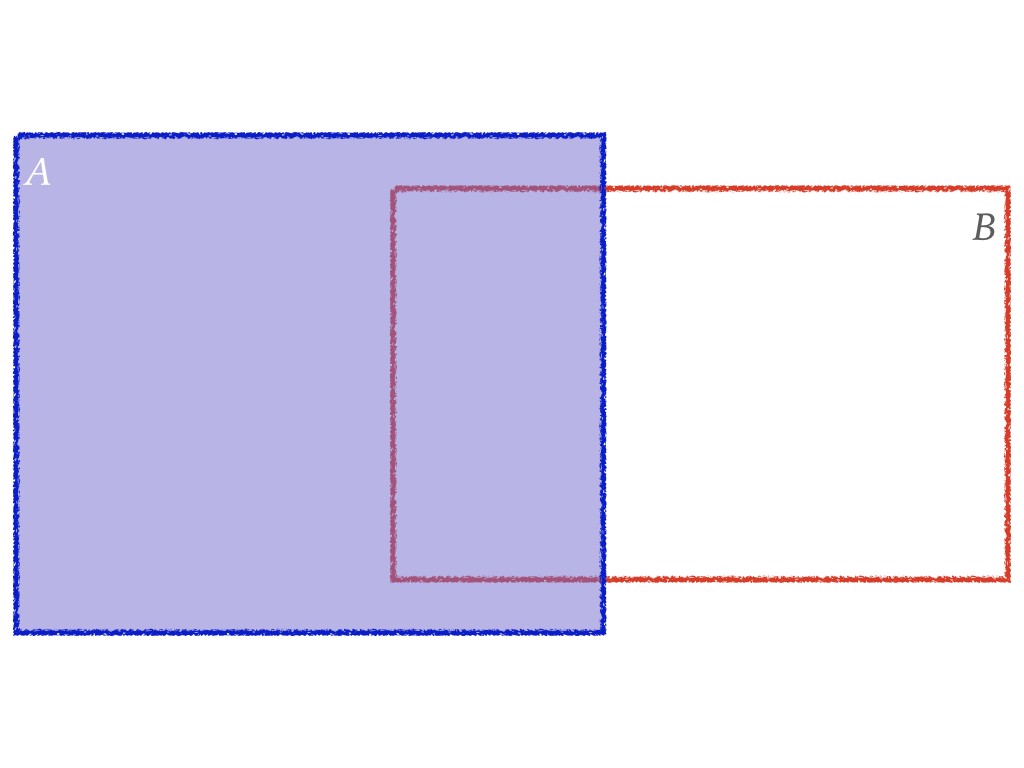
Diagram of P(A or B) (Cont.)

$$P(A\ or\ B)=P(A)+\color{red}{P(B)}\ ...$$

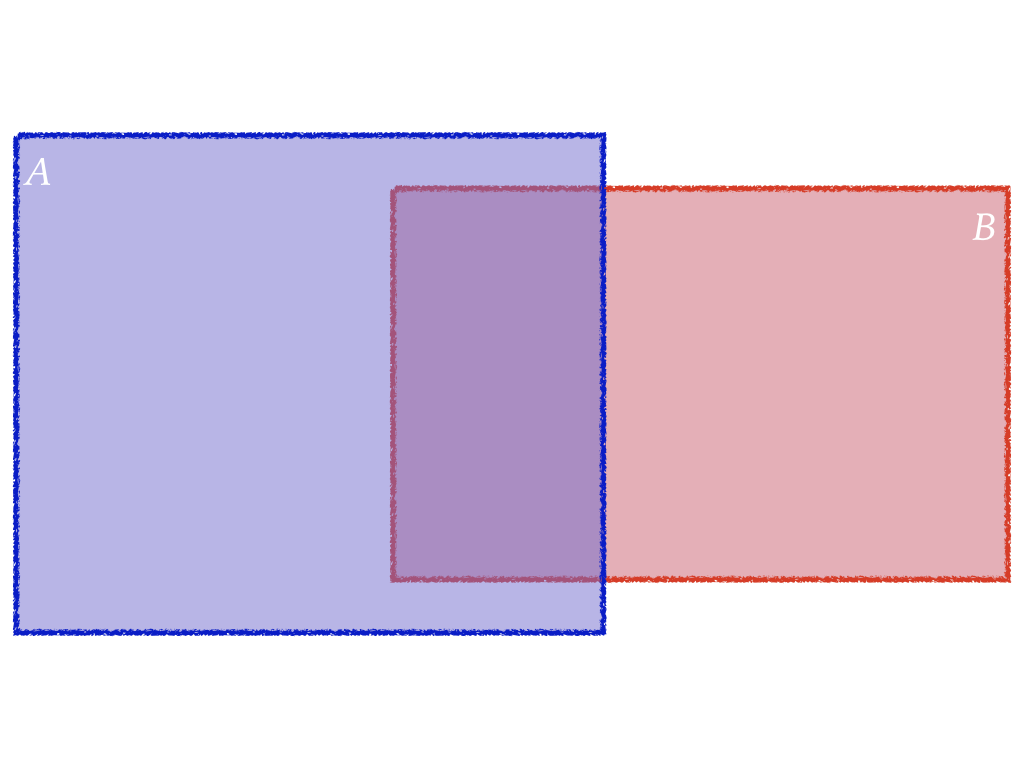
Diagram of P(A or B) (Cont.)

$$P(A\ or\ B)=P(A)+P(B)\ ...$$

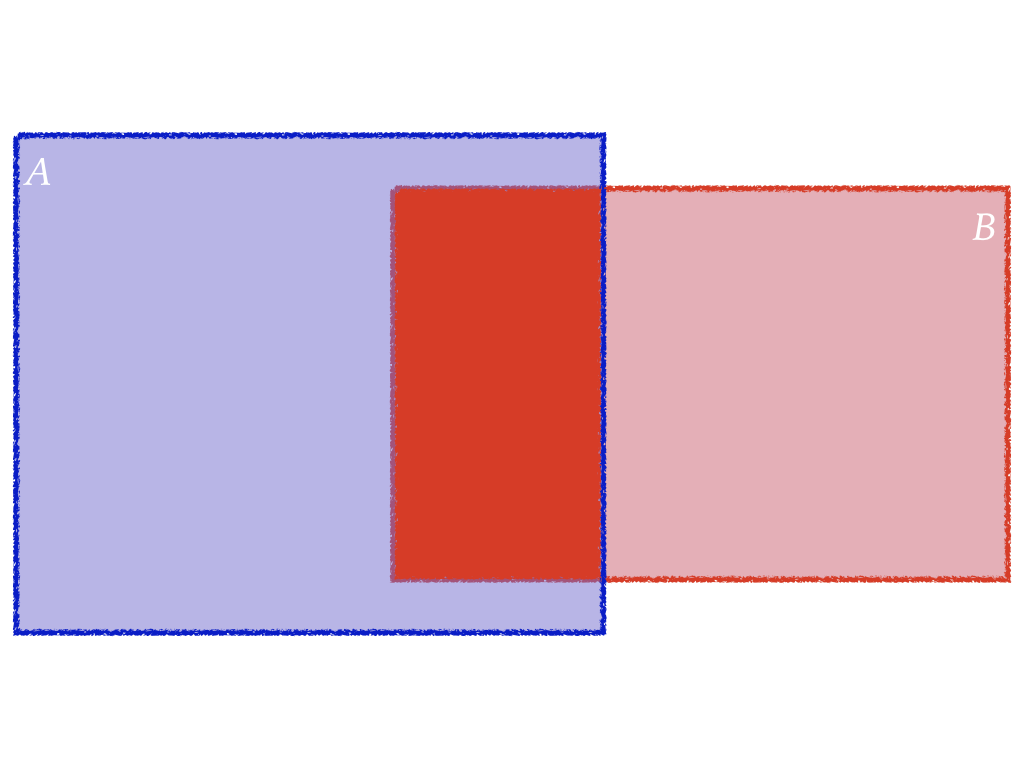
Diagram of P(A or B) (Cont.)

$$P(A\ or\ B)=P(A)+P(B)-\color{red}{P(A\ and\ B)}$$

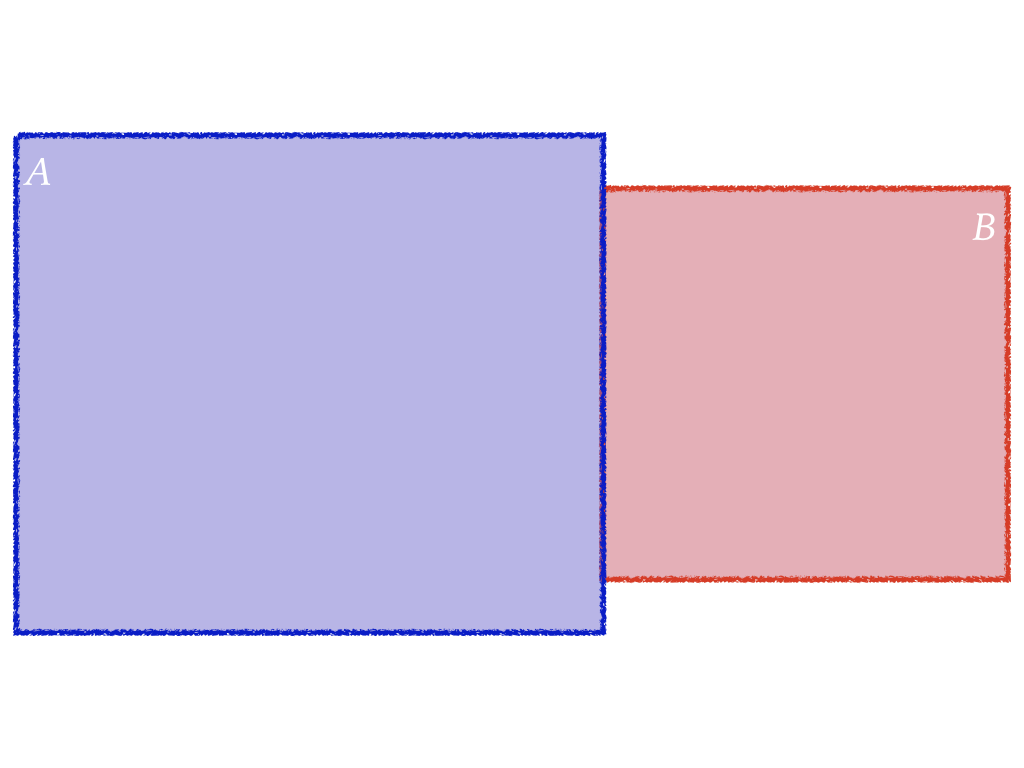
Diagram of P(A or B) (Cont.)

$$P(A\ or\ B)=P(A)+P(B)-P(A\ and\ B)$$

P(Jack or Heart) calculation in Python

P_Jack = 4/52
P_Hearts = 13/52
P_Jack_n_Hearts = 1/52
P_Jack_or_Hearts = P_Jack + P_Hearts - P_Jack_n_Hearts
print(P_Jack_or_Hearts)

0.307692307692

Let's calculate probabilities of two events

Foundations of Probability in Python