Risk-adjusted metrics
Financial Analytics in Google Sheets

David Ardia
Professor in Quantitative Methods for Finance
Sharpe ratio
Most popular risk-adjusted metric
Excess reward divided by volatility:
$$Sharpe\,\,ratio = \frac{m_G - r_f}{sd}$$
Effective rate of return: $m_G$
Risk-free rate: $r_f$
Volatility of the returns: $sd$
Sharpe ratio
Most popular risk-adjusted metric
Excess reward divided by volatility:
$$Sharpe\,\,ratio = \frac{m_G - r_f}{sd}$$
Effective rate of return: $m_G$
Risk-free rate: $r_f$ → Interest rate of the US Treasury Bill
Volatility of the returns: $sd$
Sharpe ratio
$R_1=50\%,R_2=-20\%,R_3=5\%,R_4=-3\%$
- Effective rate of return: $m_G = 5\%$
- Volatility of the returns: $sd = 30\%$
- Assume risk-free rate: $r_f = 1\%$
$$Sharpe\,\,ratio = \frac{m_G - r_f}{sd} = \frac{5\% - 1\%}{30\%} = 0.13$$
Sharpe ratio with Google Sheets
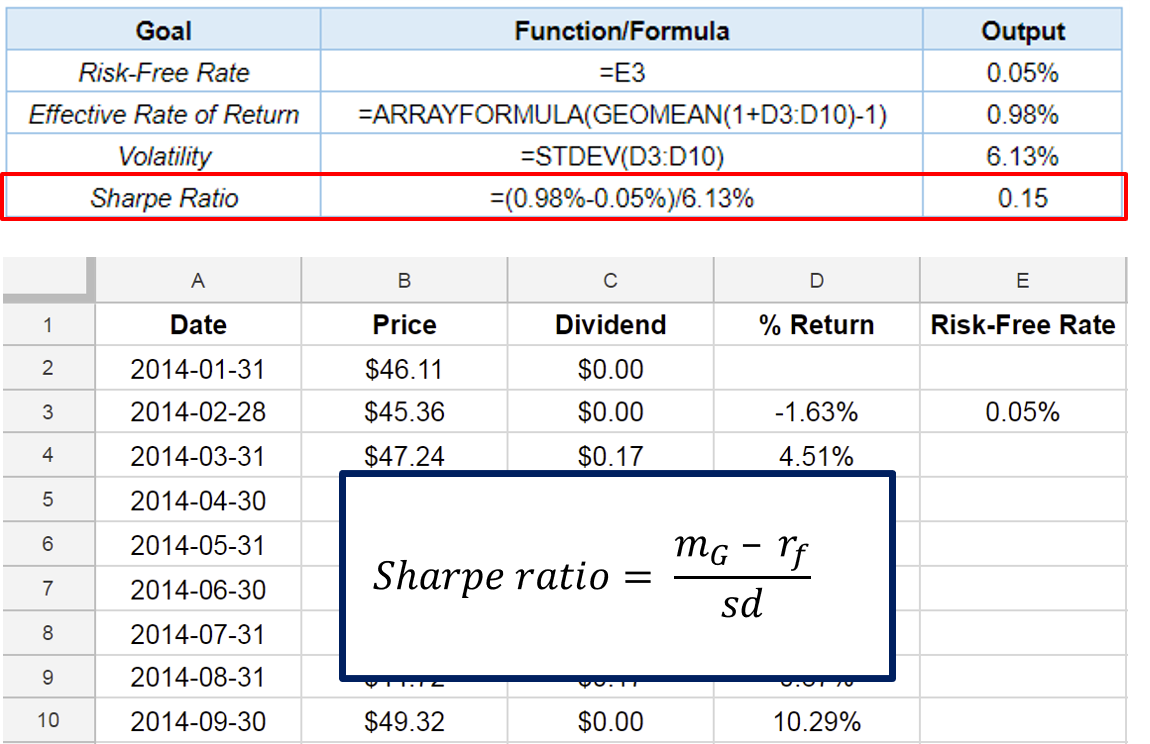
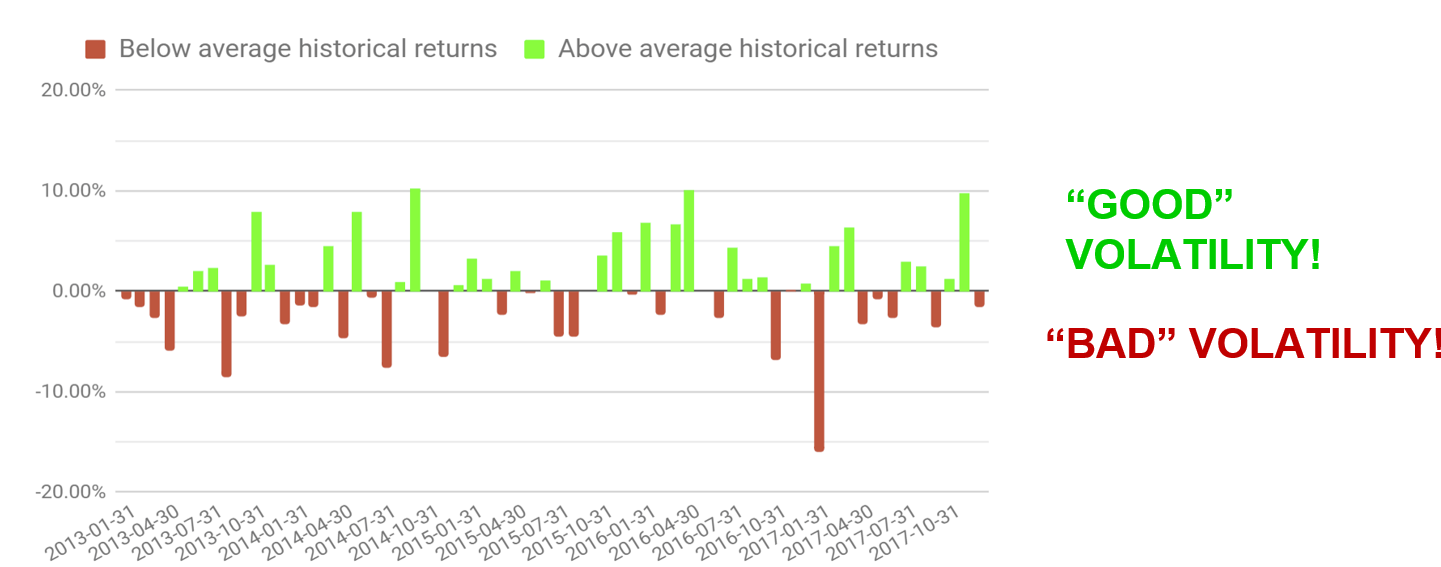
Volatility and Sharpe ratio
- High volatility penalizes the Sharpe ratio
- Is volatility bad for investors?
Semideviation and Sortino ratio
- The semideviation is a measurement of dispersion of the returns which are below the average return:
$$smd=\sqrt{\frac{(R_1^\star-m_A)^2+(R_2^\star-m_A)^2+\cdots+(R_L^\star-m_A)^2}{L}}$$
where $R_1^\star, R_2^\star,\ldots,R_L^\star$ are the $L$ historical returns which are below $m_A$
- The Sortino ratio replaces the volatility in the Sharpe ratio:
$$Sortino\,\,ratio = \frac{m_G - r_f}{ smd}$$
Semideviation and Sortino ratio
$R_1=50\%,R_2=-20\%,R_3=5\%,R_4=-3\%$
Average return: $m_A=8\%$
Semideviation:
$$smd=\sqrt{\frac{(-20\%-8\%)^2+(5\%-8\%)^2+(-3\%-8\%)^2}{3}}=17\%$$
Semideviation and Sortino ratio
$R_1=50\%,R_2=-20\%,R_3=5\%,R_4=-3\%$
- Effective rate of return: $m_G=5\%$
- Semideviation: $smd=17\%$
- Assume risk-free rate: $r_f=1\%$
$$Sortino\,\,ratio = \frac{m_G - r_f}{smd} = \frac{5\% - 1\%}{17\%} = 0.23 $$
Semideviation with Google Sheets
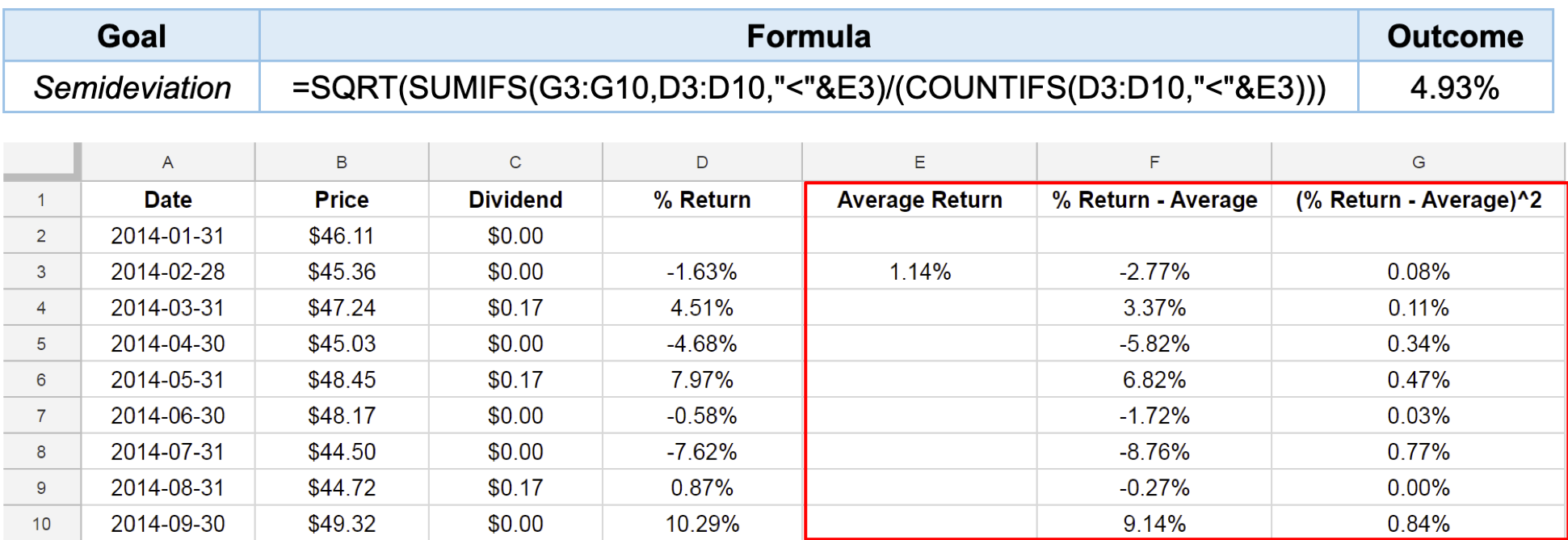
Semideviation with Google Sheets
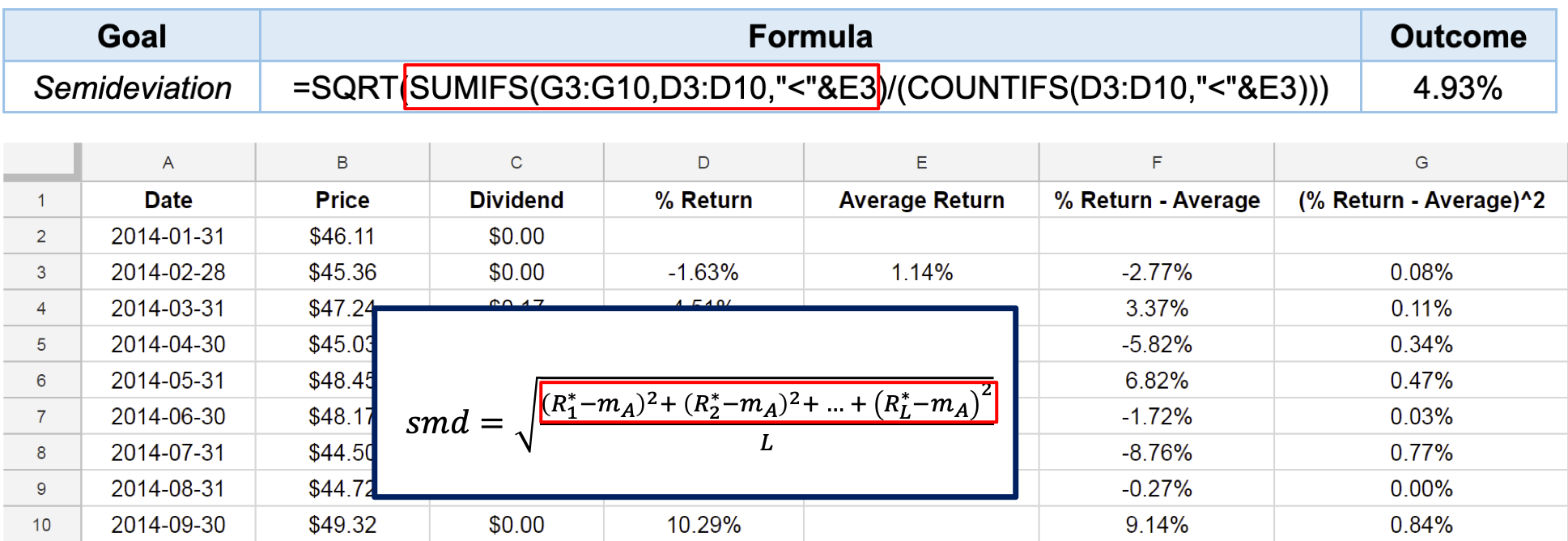
Semideviation with Google Sheets
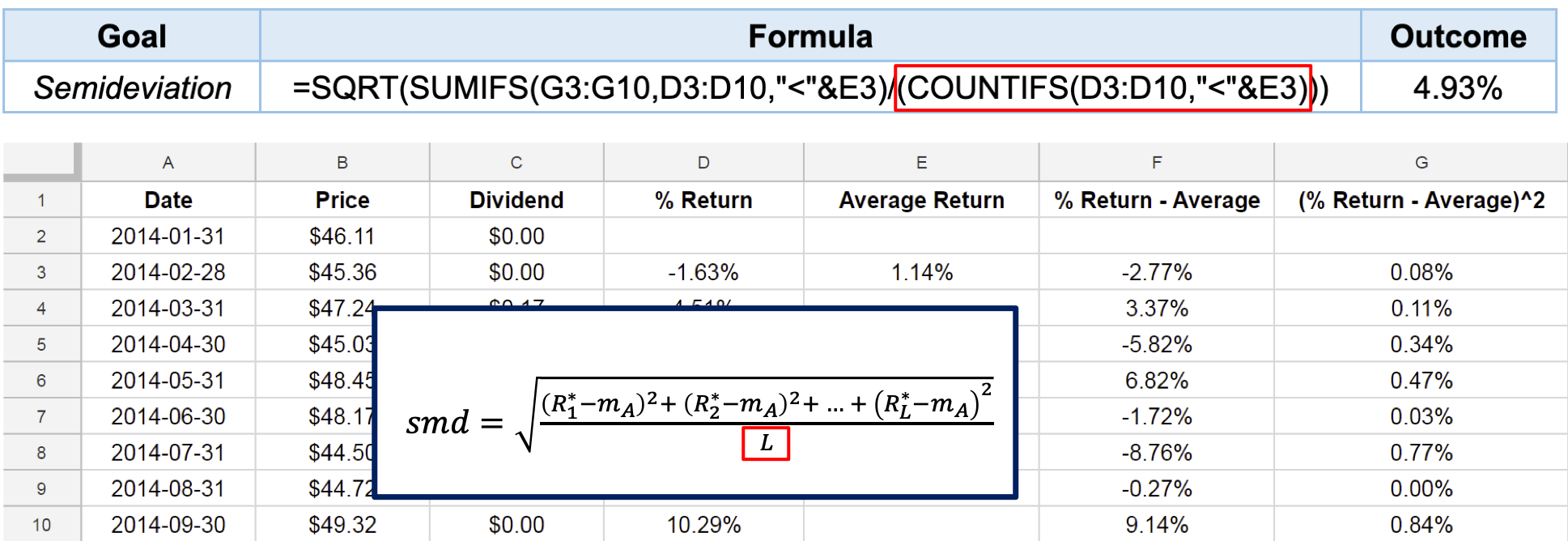
Semideviation with Google Sheets
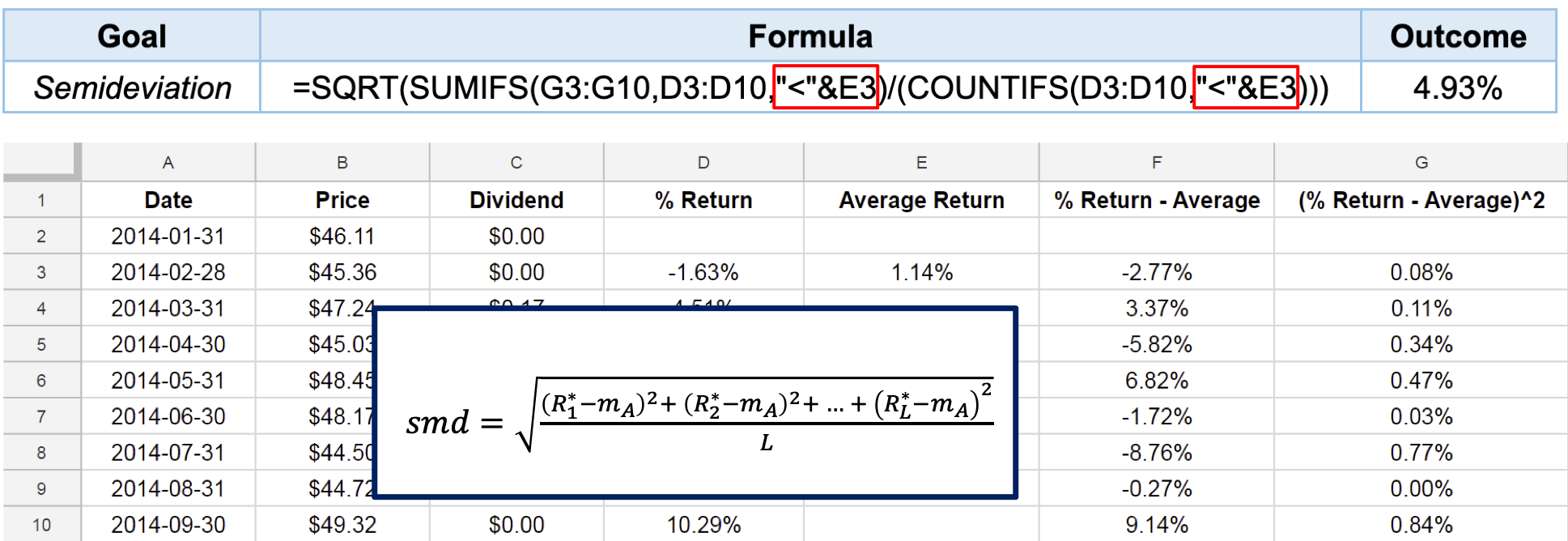
Semideviation with Google Sheets
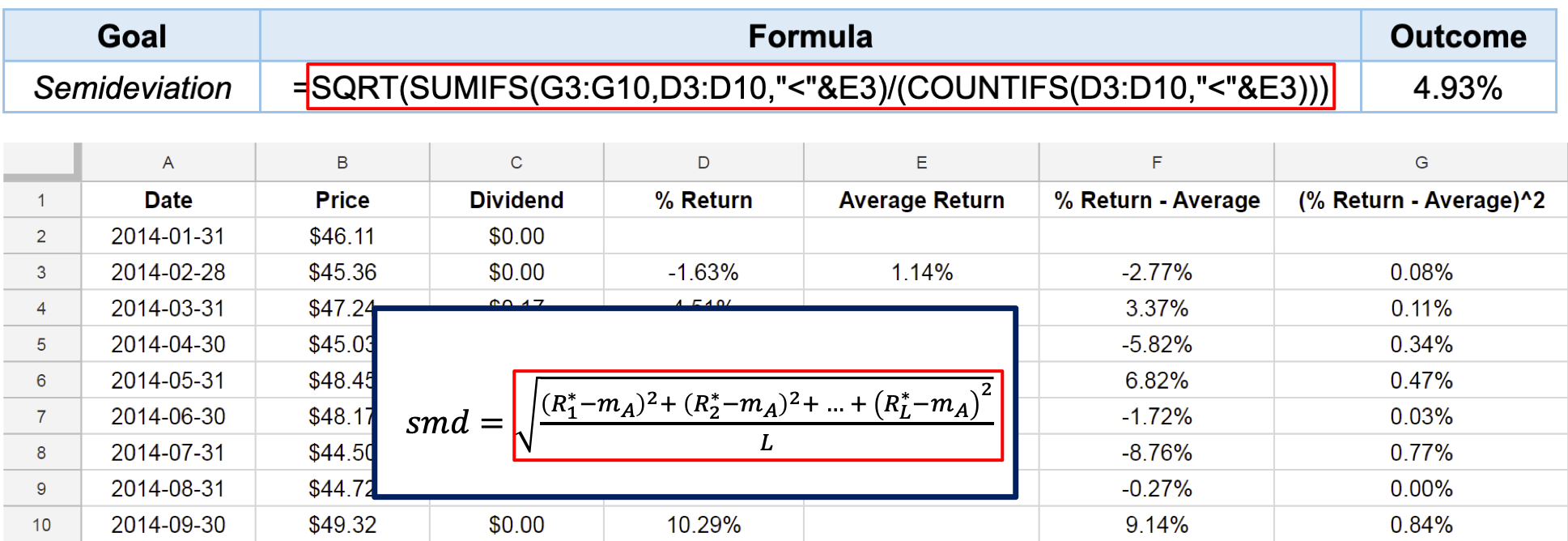
It's time to practice!
Financial Analytics in Google Sheets

