Reward metrics
Financial Analytics in Google Sheets

David Ardia
Professor in Quantitative Methods for Finance
Return on investment
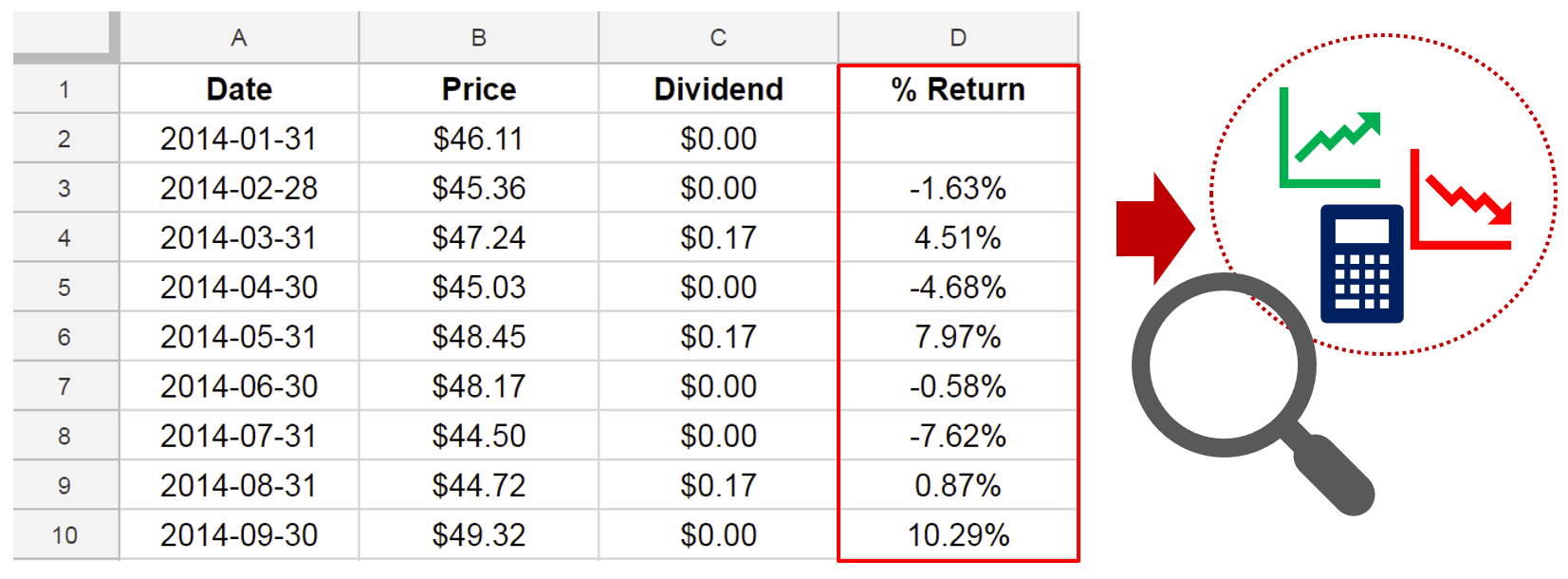
Effective rate of return
- Series of $T$ returns: $R_1,R_2,\ldots,R_T$
- Capital invested: $C$
- Effective rate of return: $R_E$
$$C(1+R_1)(1+R_2)\cdots(1+R_T)=C(1+R_E)^T$$
Effective rate of return
- After a bit of algebra:
$$R_E=[(1+R_1)\cdots(1+R_T)]^{1/T} -1$$
- Geometric mean of the series $(1+R_1),(1+R_2),\ldots,(1+R_T)$:
$$m_G=[(1+R_1)\cdots(1+R_T)]^{1/T} -1$$
Effective rate of return
$\$100$ → $\$150$ → $\$75$
$50\%$ → $-50\%$
$$m_G=[(1+50\%)(1+(-50\%))]^{1/2} -1 = -0.134=-13.4\%$$
$\$100(1+(-13.4\%))(1+(-13.4\%)) = \$75$
Average return
A popular metric to infer the expected reward is the average return:
$$m_A=\frac{R_1+R_2+\ldots+R_T}{T}$$

Average return
$\$100$ → $\$150$ → $\$75$
$50\%$ → $-50\%$
$$m_A=\frac{50\% + (-50\%)}{2}=0\%$$
Difference between effective and average return
$\$100$ → $\$150$ → $\$75$
$50\%$ → $-50\%$
- Average return: $m_A = 0\%$
→ Returns not linked to one another!
- Effective rate of return: $m_G = -13.4\%$
→ Compounding effect taken into account!
Function AVERAGE()
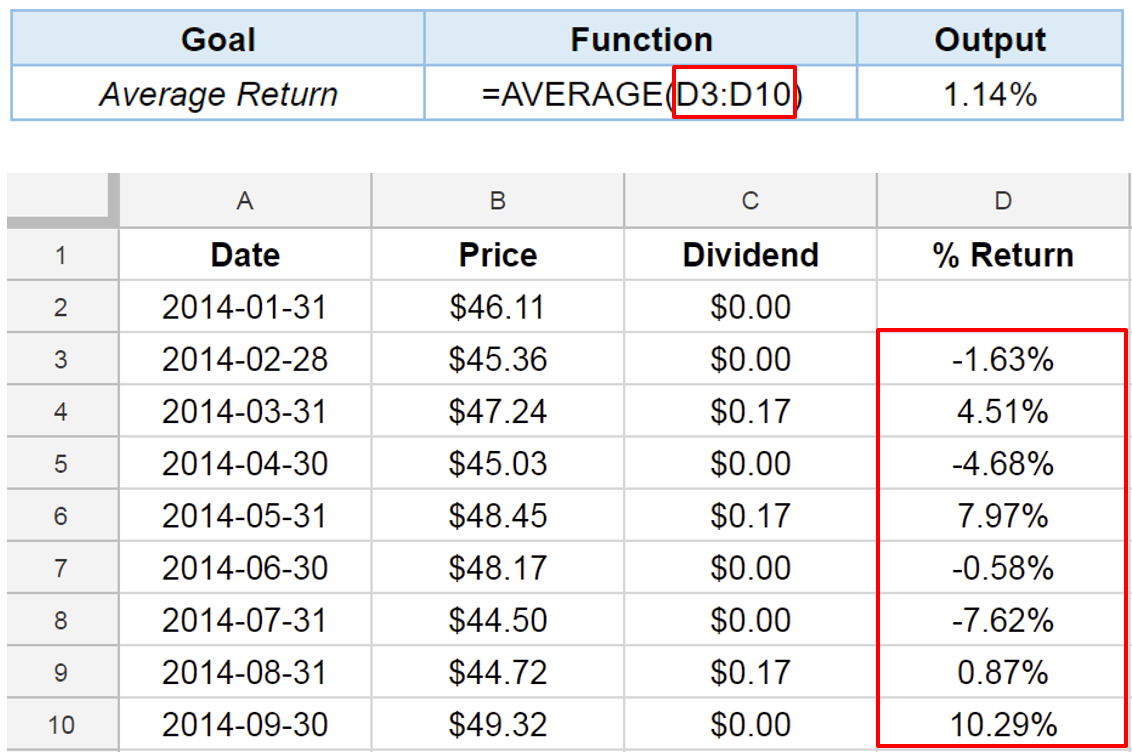
Effective rate of return: first approach
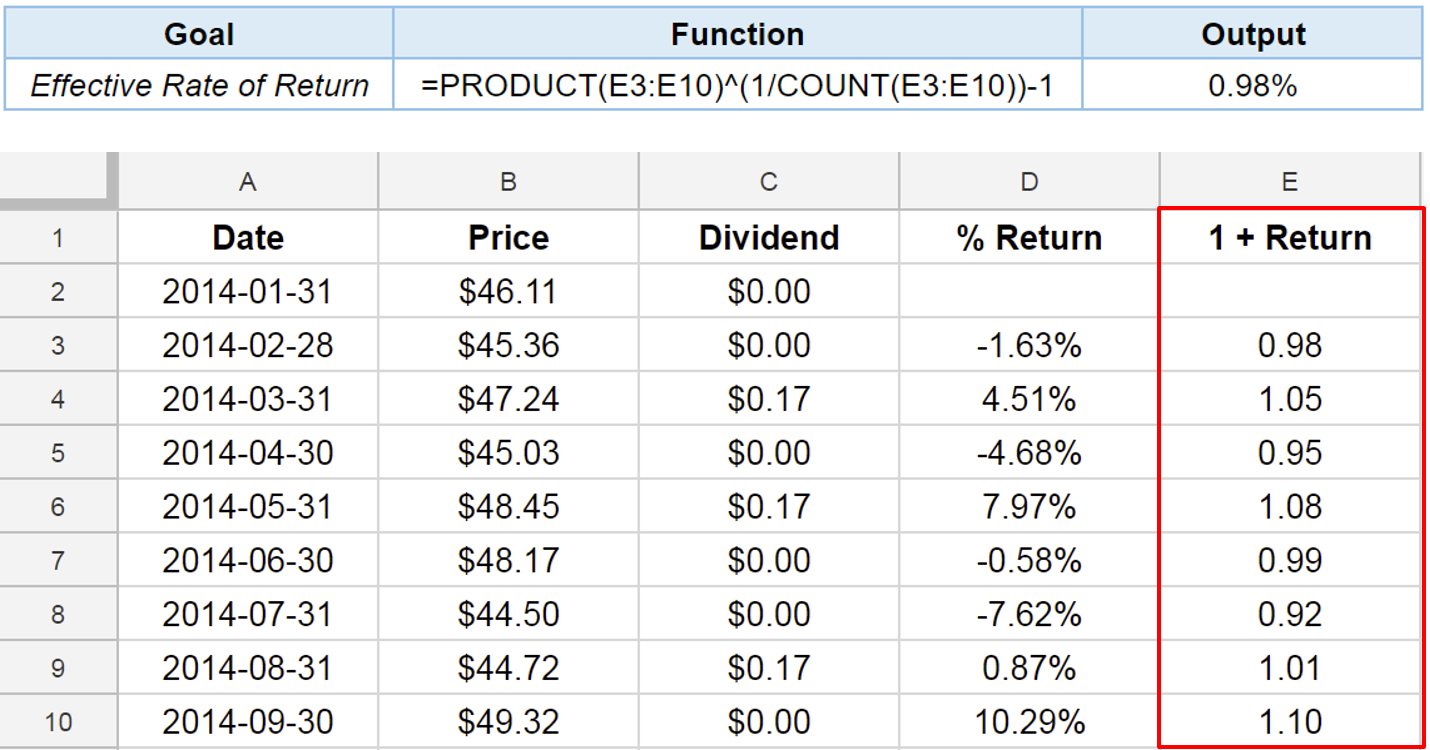
Effective rate of return: first approach
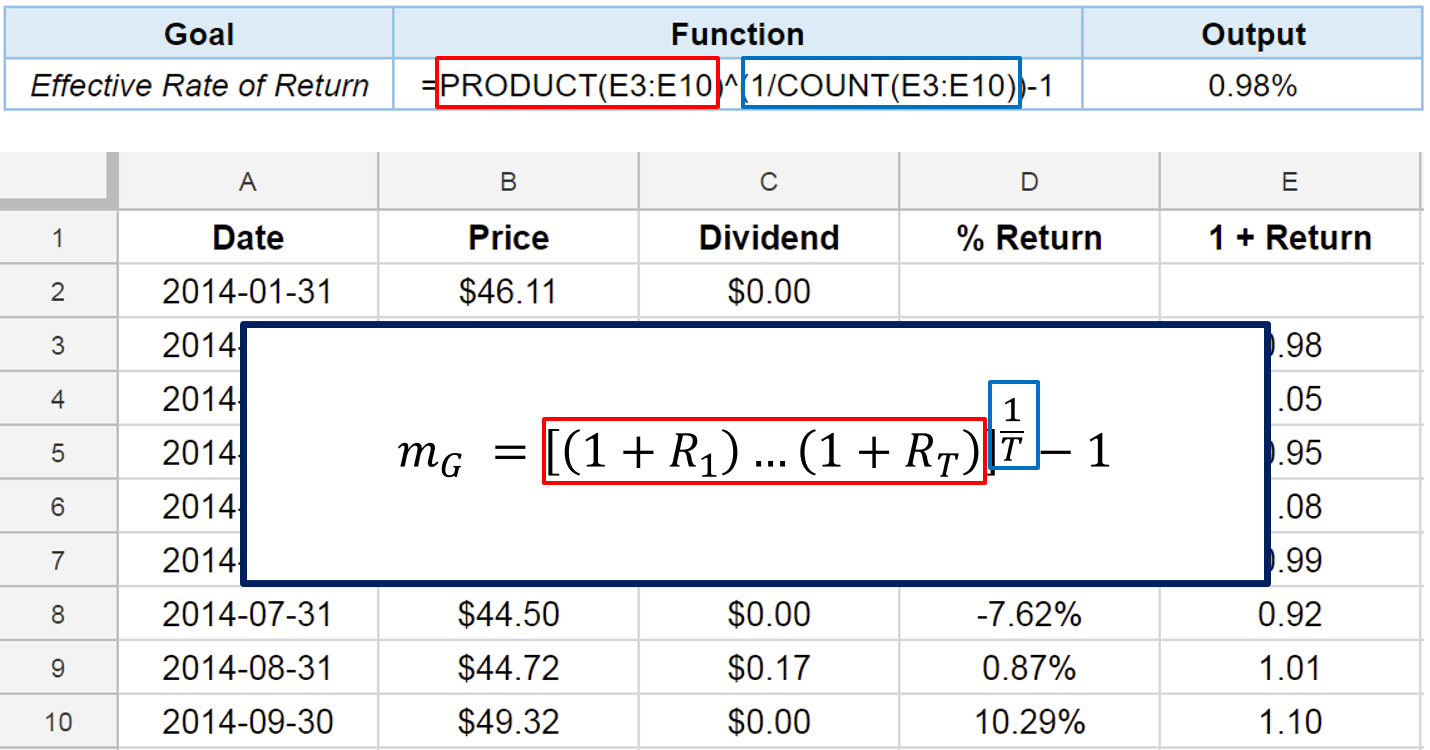
Function ARRAYFORMULA()
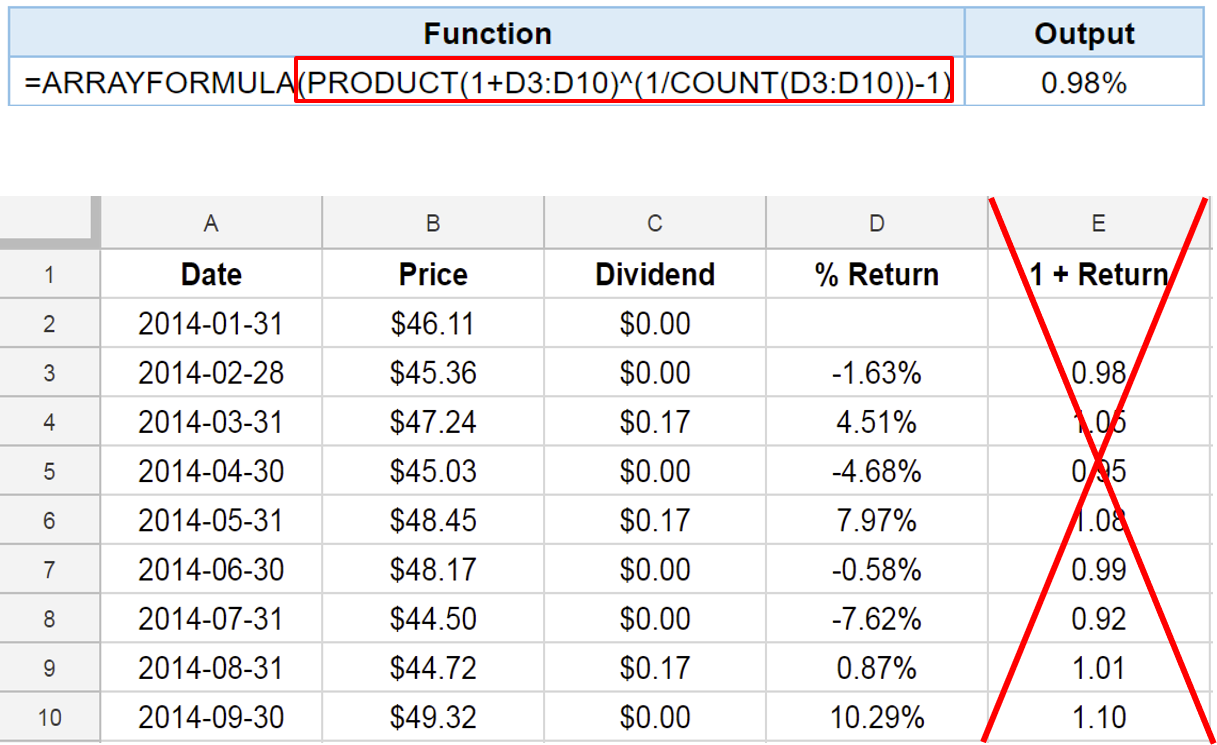
Functions ARRAYFORMULA() and GEOMEAN()
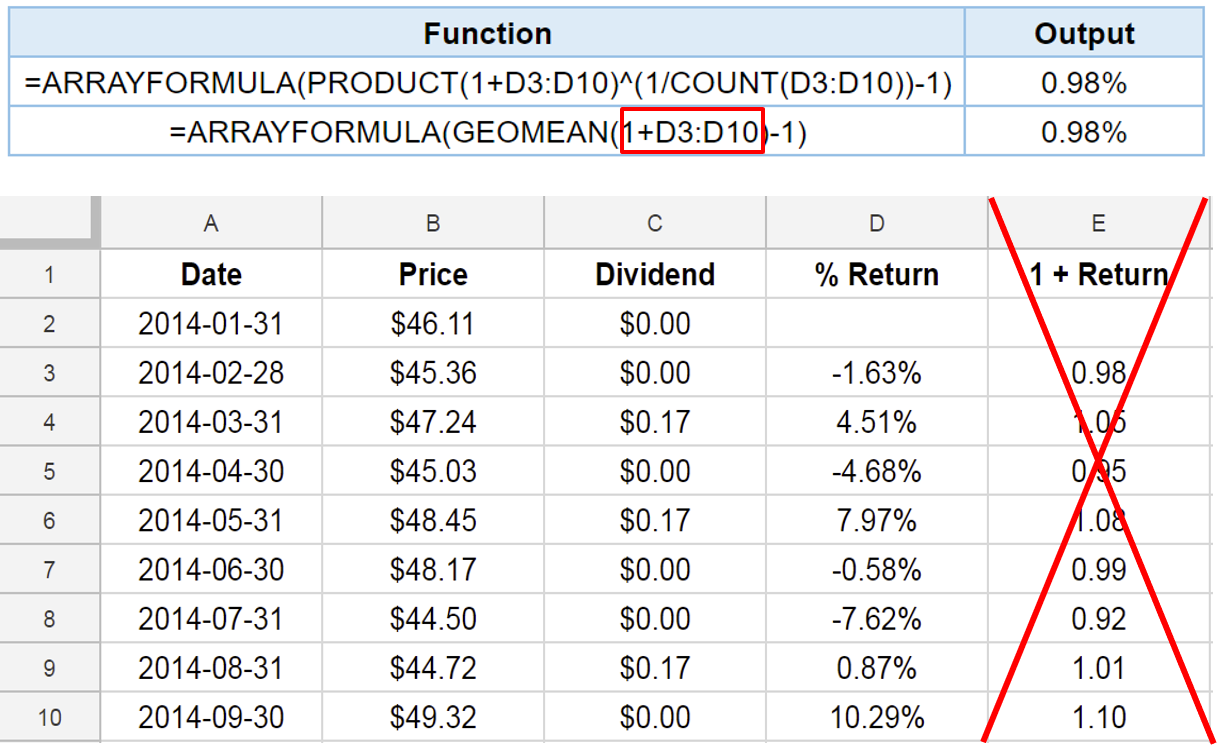
It's time to practice!
Financial Analytics in Google Sheets

