Introducing Random Search

Hyperparameter Tuning in Python

Alex Scriven

Data Scientist

What you already know

Very similar to grid search:

Define an estimator, which hyperparameters to tune and the range of values for each hyperparameter.
We still set a cross-validation scheme and scoring function

BUT we instead randomly select grid squares.

Why does this work?

Bengio & Bergstra (2012):

This paper shows empirically and theoretically that randomly chosen trials are more efficient for hyper-parameter optimization than trials on a grid.

Two main reasons:

Not every hyperparameter is as important
A little trick of probability

A probability trick

A grid search:

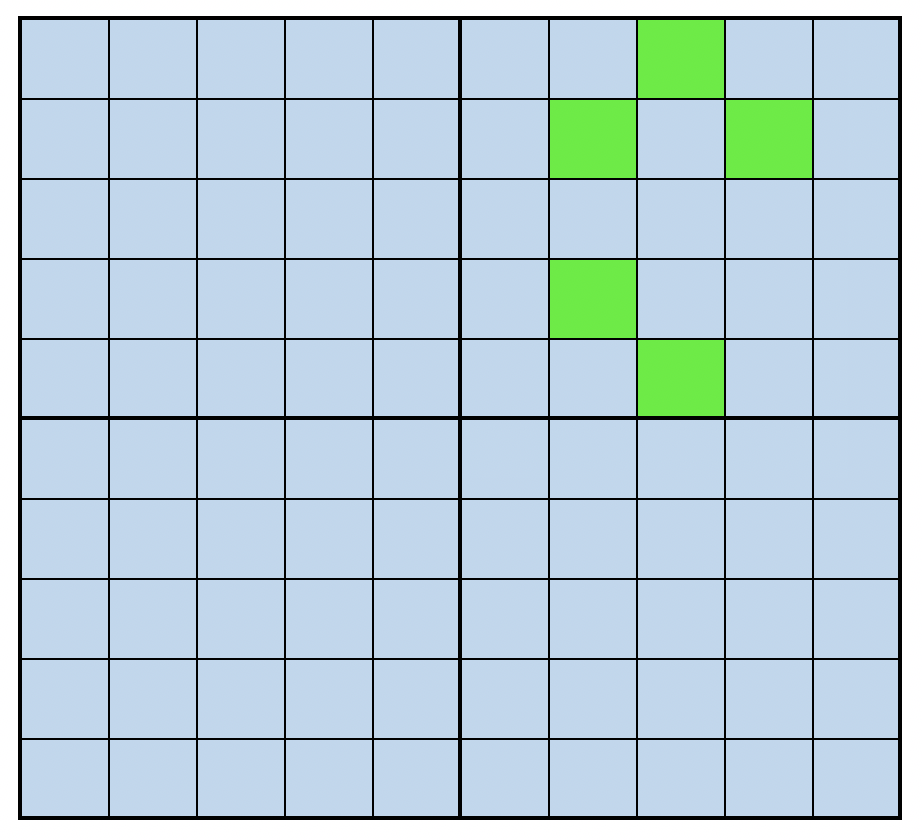
10x10 of different models

How many models must we run to have a 95% chance of getting one of the green squares?

Our best models:

10x10 of different models

A probability Trick

If we randomly select hyperparameter combinations uniformly, let's consider the chance of MISSING every single trial, to show how unlikely that is

Trial 1 = 0.05 chance of success and (1 - 0.05) of missing
- Trial 2 = (1-0.05) x (1-0.05) of missing the range
  - Trial 3 = (1-0.05) x (1-0.05) x (1-0.05) of missing again
In fact, with n trials we have (1-0.05)^n chance that every single trial misses that desired spot.

A probability trick

So how many trials to have a high (95%) chance of getting in that region?

We have (1-0.05)^n chance to miss everything.
So we must have (1- miss everything) chance to get in there or (1-(1-0.05)^n)
Solving 1-(1-0.05)^n >= 0.95 gives us n >= 59

A probability trick

What does that all mean?

You are unlikely to keep completely missing the 'good area' for a long time when randomly picking new spots
A grid search may spend lots of time in a 'bad area' as it covers exhaustively.

Some important notes

Remember:

The maximum is still only as good as the grid you set!
Remember to fairly compare this to grid search, you need to have the same modeling 'budget'

Creating a random sample of hyperparameters

We can create our own random sample of hyperparameter combinations:

# Set some hyperparameter lists
learn_rate_list = np.linspace(0.001,2,150)
min_samples_leaf_list = list(range(1,51))

# Create list of combinations
from itertools import product
combinations_list = [list(x) for x in 
                    product(learn_rate_list, min_samples_leaf_list)]

# Select 100 models from our larger set
random_combinations_index = np.random.choice(
                            range(0,len(combinations_list)), 100, 
                            replace=False)
combinations_random_chosen = [combinations_list[x] for x in 
                            random_combinations_index]

Visualizing a Random Search

We can also visualize the random search coverage by plotting the hyperparameter choices on an X and Y axis.

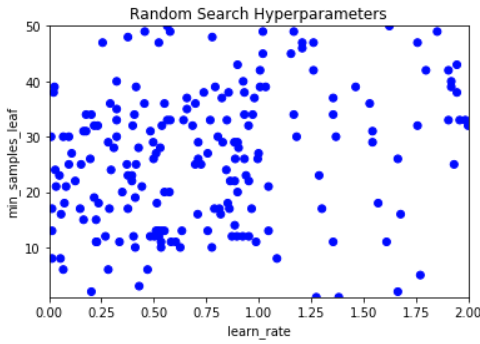
random search coverage graph

Notice how this has a wide range of the scatter but not deep coverage?

Let's practice!

Hyperparameter Tuning in Python