Going beyond linear regression

Generalized Linear Models in Python

Ita Cirovic Donev

Data Science Consultant

Course objectives

  • Learn building blocks of GLMs
  • Train GLMs
  • Interpret model results
  • Assess model performance
  • Compute predictions
  • Chapter 1: How are GLMs an extension of linear models
  • Chapter 2: Binomial (logistic) regression
  • Chapter 3: Poisson regression
  • Chapter 4: Multivariate logistic regression
Generalized Linear Models in Python

Review of linear models

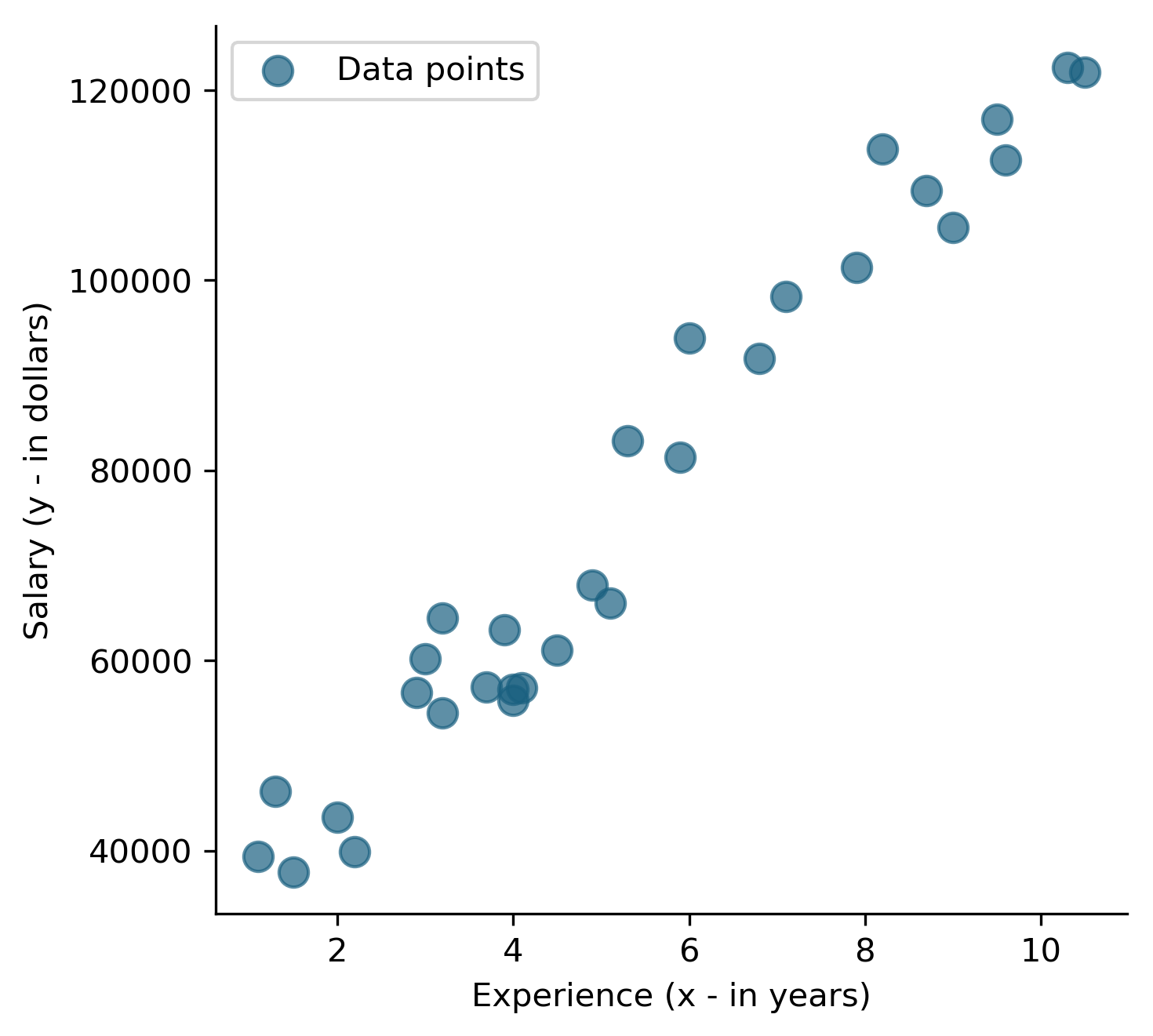
Scatterplot of years of experience and salary.

$\color{#00A388}{\text{salary}} \sim \color{#FF6138}{\text{experience}}$

$\normalsize{\color{#00A388}{\text{salary}} = \beta_0 + \beta_1\times\color{#FF6138}{\text{experience}} + \epsilon}$

$\normalsize{\color{#00A388}y = \beta_0 + \beta_1x_1 + \epsilon}$

Generalized Linear Models in Python

Review of linear models

Scatterplot of years of experience and salary.

$\color{#00A388}{\text{salary}} \sim \color{#FF6138}{\text{experience}}$

$\color{#00A388}{\text{salary}} = \beta_0 + \beta_1\times{\text{experience}} + \epsilon$

$\color{#00A388}y = \beta_0 + \beta_1x_1 + \epsilon$

where:
$\color{#00A388}y$ - response variable (output)

Generalized Linear Models in Python

Review of linear models

Scatterplot of years of experience and salary.

$\color{#00A388}{\text{salary}} \sim \color{#FF6138}{\text{experience}}$

$\normalsize{\color{#00A388}{\text{salary}} = \beta_0 + \beta_1\times\color{#FF6138}{\text{experience}} + \epsilon}$

$\normalsize{\color{#00A388}y = \beta_0 + \beta_1\color{#FF6138}{x_1} + \epsilon}$

where:
$y$ - response variable (output)
$\color{#FF6138}x$ - explanatory variable (input)

Generalized Linear Models in Python

Review of linear models

Scatterplot of years of experience and salary.

$\color{#00A388}{\text{salary}} \sim \color{#FF6138}{\text{experience}}$

$\normalsize{\color{#00A388}{\text{salary}} = \color{#007AFF}{\beta_0} + \color{#007AFF}{\beta_1}\times\color{#FF6138}{\text{experience}} + \epsilon}$

$\normalsize{\color{#00A388}y = \color{#007AFF}{\beta_0} + \color{#007AFF}{\beta_1}\color{#FF6138}{x_1} + \epsilon}$

where:
$y$ - response variable (output)
$x$ - explanatory variable (input)
$\color{#007AFF}{\beta}$ - model parameters
$\color{#007AFF}{\beta_0}$ - intercept
$\color{#007AFF}{\beta_1}$ - slope

Generalized Linear Models in Python

Review of linear models

Scatterplot of years of experience and salary.

$\color{#00A388}{\text{salary}} \sim \color{#FF6138}{\text{experience}}$

$\normalsize{\color{#00A388}{\text{salary}} = \color{#007AFF}{\beta_0} + \color{#007AFF}{\beta_1}\times\color{#FF6138}{\text{experience}} + \color{#B12BFF}\epsilon}$

$\normalsize{\color{#00A388}y = \color{#007AFF}{\beta_0} + \color{#007AFF}{\beta_1}\color{#FF6138}{x_1} + \color{#B12BFF}\epsilon}$

where:
$y$ - response variable (output)
$x$ - explanatory variable (input)
$\color{#007AFF}{\beta}$ - model parameters
$\color{#007AFF}{\beta_0}$ - intercept
$\color{#007AFF}{\beta_1}$ - slope
$\color{#B12BFF}{\epsilon}$ - random error

Generalized Linear Models in Python

LINEAR MODEL - ols()

from statsmodels.formula.api import ols

model = ols(formula = 'y ~ X', 
            data = my_data).fit()

GENERALIZED LINEAR MODEL - glm()

import statsmodels.api as sm
from statsmodels.formula.api import glm

model = glm(formula = 'y ~ X', 
            data = my_data,
            family = sm.families.____).fit()
Generalized Linear Models in Python

Assumptions of linear models

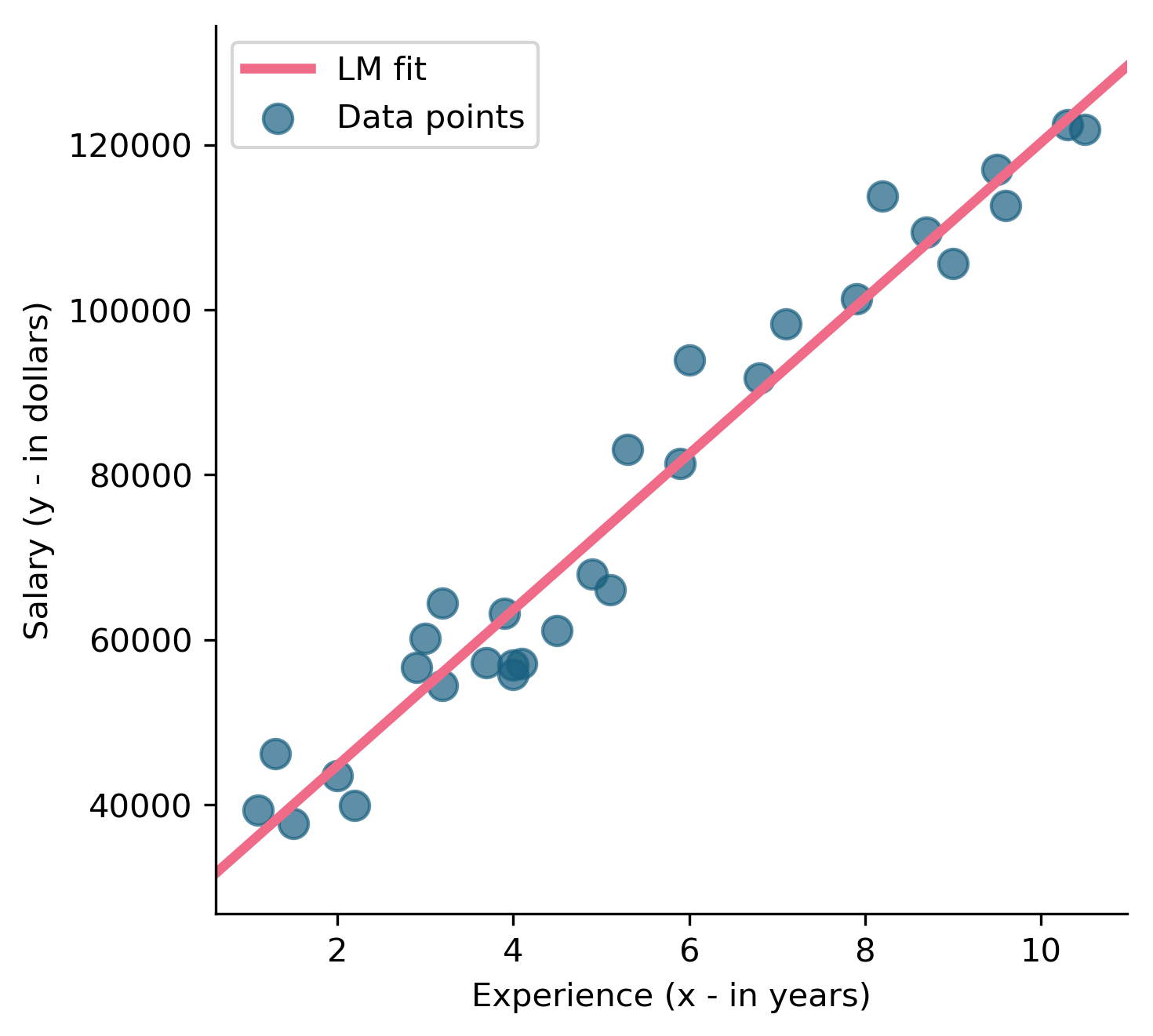
Linear fit to the data of years of experience and salary.

$$ \normalsize{{\text{salary} = \color{blue}{25790} + \color{blue}{9449}\times\text{experience}}} $$

Regression function

$\normalsize{E[y] = \mu = \beta_0 + \beta_1x_1}$

Assumptions

  • Linear in parameters
  • Errors are independent and normally distributed
  • Constant variance
Generalized Linear Models in Python

What if ... ?

  • The response is binary or count $\rightarrow \color{red}{\text{NOT continuous}}$

Displot of continuous, binary and Poisson random variable.

  • The variance of $y$ is not constant $\rightarrow \color{red}{\text{depends on the mean}}$
Generalized Linear Models in Python

Dataset - nesting of horseshoe crabs

Variable Name Description
sat Number of satellites residing in the nest
y There is at least one satellite residing in the nest; 0/1
weight Weight of the female crab in kg
width Width of the female crab in cm
color 1 - light medium, 2 - medium, 3 - dark medium, 4 - dark
spine 1 - both good, 2 - one worn or broken, 3 - both worn or broken
1 A. Agresti, An Introduction to Categorical Data Analysis, 2007.
Generalized Linear Models in Python

Linear model and binary response

 

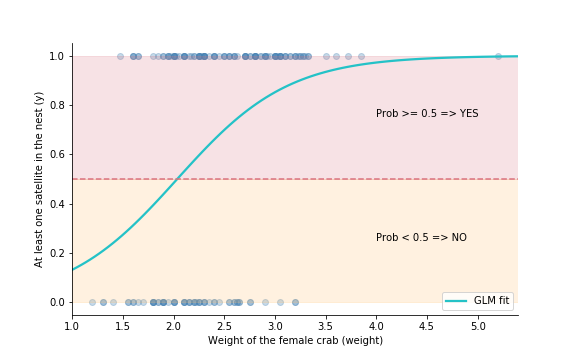
$\text{satellite crab} \sim \text{female crab weight}$

y ~ weight

$P(\text{satellite crab is present})=P(y=1)$

Generalized Linear Models in Python

Linear model and binary response

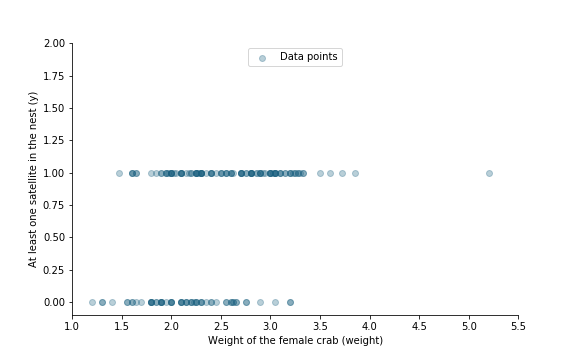
Scatterplot of female crab weight and the response (at least one satellite nearby).

Generalized Linear Models in Python

Linear model and binary response

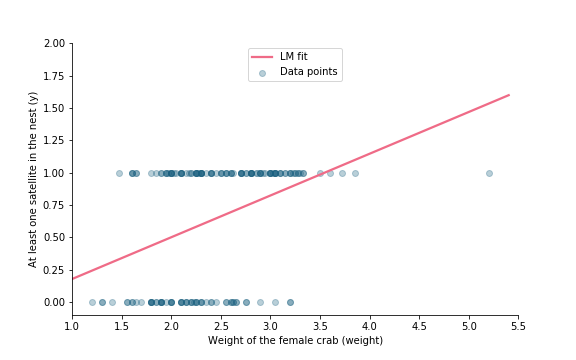
Linear fit to the data of female crab weight and the response (at least one satellite nearby).

Generalized Linear Models in Python

Linear model and binary response

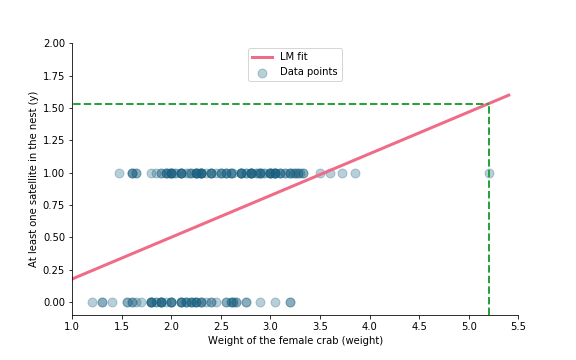
Reading off probability value for the linear model fit of female crab weight and the response (at least one satellite nearby).

Generalized Linear Models in Python

Linear model and binary data

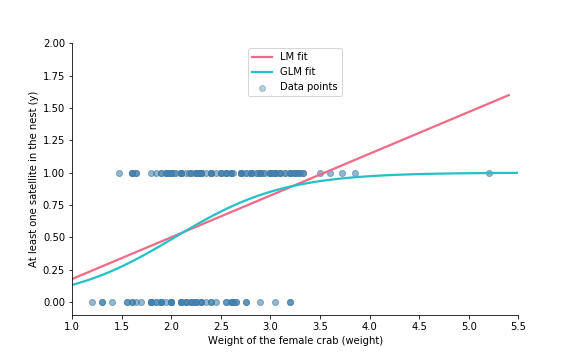
Adding GLM (Binomial) fit to the linear fit to the data of female crab weight and the response (at least one satellite nearby).

Generalized Linear Models in Python

Linear model and binary data

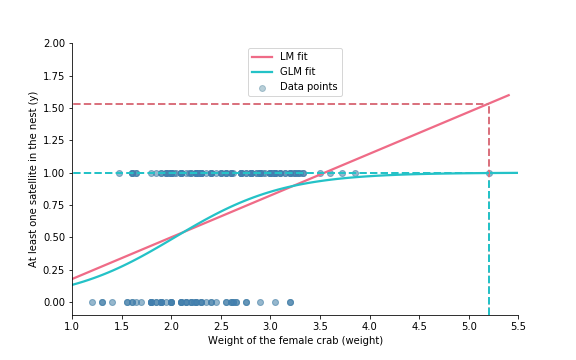
Reading off probability value for the GLM (Binomial) model fit of female crab weight and the response (at least one satellite nearby).

Generalized Linear Models in Python

From probabilities to classes

Separation of model output given defined probability value cutoff.

Generalized Linear Models in Python

Let's practice!

Generalized Linear Models in Python

Preparing Video For Download...