Computing and describing predictions

Generalized Linear Models in Python

Ita Cirovic Donev

Data Science Consultant

Computing predictions

After obtaining model fit

  1. Fitted values for original $x$ values

Diagram of the model fitting process.

Generalized Linear Models in Python

Computing predictions

After obtaining model fit

  1. fitted values for original $x$ values

  2. New values of $x$ for predicted values

Diagram of the model fitting process and computing predictions.

Generalized Linear Models in Python

Computing predictions

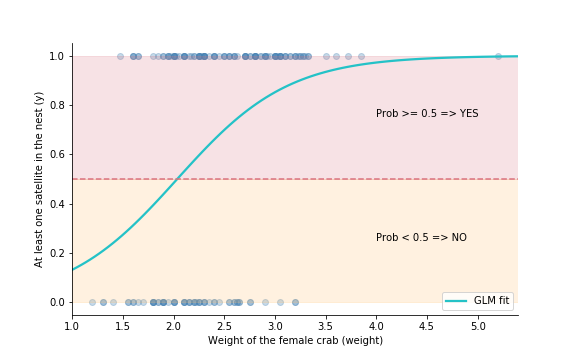
  • Horseshoe crab model y ~ weight $$ \mu = \frac{\exp(-3.6947+1.8151 \times weight)}{1+\exp(-3.6947+1.8151 \times weight)} $$

  • New measurement: weight = 2.85

$$ \mu = \frac{\exp(-3.6947+1.8151 \times \color{blue}{2.85})}{1+\exp(-3.6947+1.8151 \times \color{blue}{2.85})} = 0.814 $$

Generalized Linear Models in Python

Predictions in Python

  • Compute model predictions for dataset new_data
    # Compute model predictions
model_GLM.predict(exog = new_data)
Generalized Linear Models in Python

From probabilities to classes

Separation of model output given defined probability value cutoff.

Generalized Linear Models in Python

Computing class predictions

# Extract fitted probabilities from model
crab['fitted'] = model.fittedvalues.values

# Define cut-off value
cut_off = 0.4

# Compute class predictions
crab['pred_class'] = np.where(crab['fitted'] > cut_off, 1, 0)
Generalized Linear Models in Python

Computing class predictions

# Count occurences for each class
crab['pred_class'].value_counts()

1    151
0     22
Cut-off $\hat y=1$ $\hat y=0$
$\mu = 0.4$ 151 22
$\mu = 0.5$ 126 47
Generalized Linear Models in Python

Confusion matrix

Empty confusion matrix.

Generalized Linear Models in Python

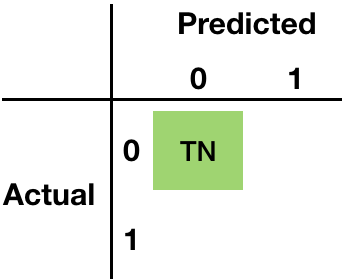
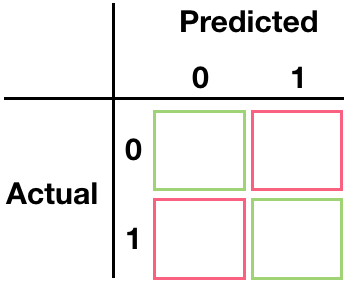
Confusion matrix - True Negatives

Presentation of true negatives in the confusion matrix.

Generalized Linear Models in Python

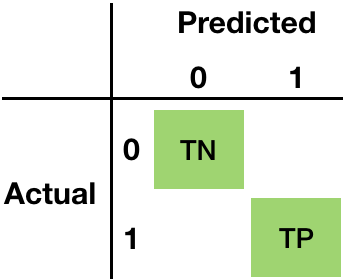
Confusion matrix - True Positives

Presentation of true negatives and true positives in the confusion matrix.

Generalized Linear Models in Python

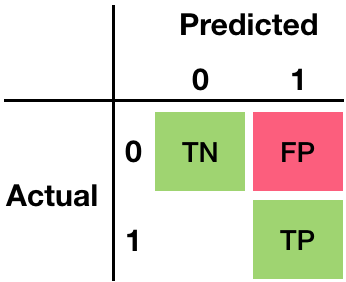
Confusion matrix - False Positives

Presentation of true negatives, true positives and false positives in the confusion matrix.

Generalized Linear Models in Python

Confusion matrix - False Negatives

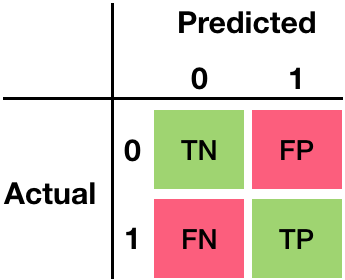
Presentation of true negatives, true positives, false positives and false negatives in the confusion matrix.

Generalized Linear Models in Python

Confusion matrix in Python

print(pd.crosstab(y_actual, y_predicted, 
            rownames=['Actual'], colnames=['Predicted'], 
            margins = True))

Predicted   0    1  All
Actual                 
0          15   47   62
1           7  104  111
All        22  151  173
Generalized Linear Models in Python

Let's practice!

Generalized Linear Models in Python

Preparing Video For Download...