Binary data and logistic regression
Generalized Linear Models in Python

Ita Cirovic Donev
Data Science Consultant
Binary response data
- Two-class response $\rightarrow \large{\texttt{\color{#079EA1}{0},\color{#ED715F}{1}}}$
Examples:
- Credit scoring $\rightarrow \texttt{\color{#ED715F}{"Default"}/\color{#079EA1}{"Non-Default"}}$
- Passing a test $\rightarrow \texttt{\color{#079EA1}{"Pass"}/\color{#ED715F}{"Fail"}}$
- Fraud detection $\rightarrow \texttt{\color{#ED715F}{"Fraud"}/\color{#079EA1}{"No-Fraud"}}$
- Choice of a product $\rightarrow \texttt{\color{#2485F2}{"Product ABC"}/\color{#F2AC30}{"Product XYZ"}}$
Binary data
UNGROUPED
- Single event
- Flip one coin
- Two of possible outcomes: 0/1
- $Bernoulli(p)$ or
- $Binomial(n=1,p)$
GROUPED
- Multiple events
- Flip multiple coins
- Number of successes in a given $n$ number of trials
- $Binomial(n,p)$
Logistic function
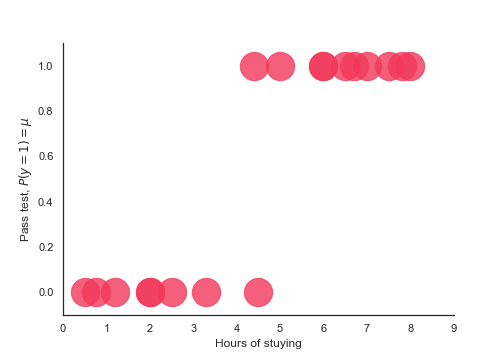
Logistic function
Test outcome: $PASS=1$ or $FAIL=0$
Want to model
$P(y=1)=\beta_0 + \beta_1x_1$
$P(\text{Pass})=\beta_0 + \beta_1 \times \text{Hours of study}$
Logistic function
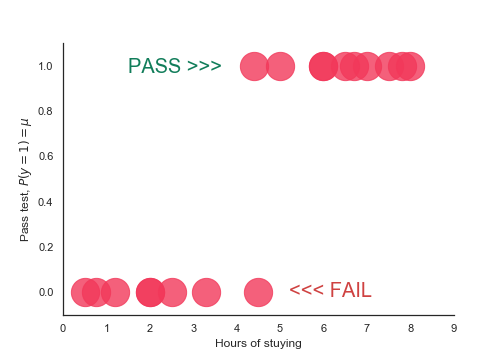
Test outcome: $PASS=1$ or $FAIL=0$
Want to model
$P(y=1)=\beta_0 + \beta_1x_1$
$P(\text{Pass})=\beta_0 + \beta_1 \times \text{Hours of study}$
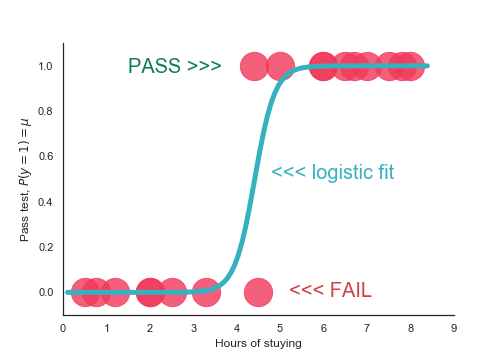
- Use logistic function
$f(z) = \frac{1}{(1+\exp(-z))}$
Odds and odds ratio
$$ ODDS = \frac{\text{event occuring}}{\text{event NOT occuring}} $$
$$ \text{ODDS RATIO} = \frac{odds 1}{odds 2} $$
Odds example
4 games

Odds are 3 to 1

Odds and probabilities
$$ \text{odds} \neq \text{probability} $$
$$ \text{odds} = \frac{\text{probability}}{1-\text{probability}} $$
$$ \text{probability} = \frac{\text{odds}}{1+\text{odds}} $$
From probability model to logistic regression
Step 1. Probability model
$E(y)=\mu=P(y=1)=\beta_0 + \beta_1x_1$
Step 2. Logistic function
$f(z) = \large{\frac{1}{(1+\exp(-z))}}$
Step 3. Apply logistic function $\rightarrow$ INVERSE-LOGIT
$\mu = \large{\frac{1}{1+\exp(-(\beta_0+\beta_1x_1))}} = \large{\frac{\exp(\beta_0+\beta_1x_1)}{1+\exp(\beta_0+\beta_1x_1)}}$
$1-\mu = \large{\frac{1}{1+\exp(\beta_0+\beta_1x_1)}}$
From probability model to logistic regression
- Probability $\rightarrow$ odds $$ ODDS=\frac{\mu}{1-\mu} = exp{(\beta_0+\beta_1x_1)} $$
- Log transformation $\rightarrow \color{#CF5383}{\text{LOGISTIC REGRESSION}}$
$$ LOGIT(\mu)=log(\frac{\mu}{1-\mu}) = \beta_0+\beta_1x_1 $$
Logistic regression in Python
Function - glm()
model_GLM = glm(formula = 'y ~ x',
data = my_data,
family = sm.families.Binomial()).fit
Input
y = [0,1,1,0,...]
y = ['No','Yes','Yes',...]
y = ['Fail','Pass','Pass',...]
Let's practice!
Generalized Linear Models in Python

