Interpreting coefficients

Generalized Linear Models in Python

Ita Cirovic Donev

Data Science Consultant

Model coefficients

Statistical summary of the fitted model, with highlighted coef column.

Generalized Linear Models in Python

Coefficient beta

  • $\beta > 0 \rightarrow$ ascending curve

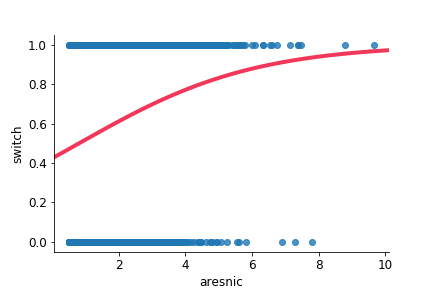
Logistic model fit of arsenic and switch.

  • $\beta < 0 \rightarrow$ descending curve

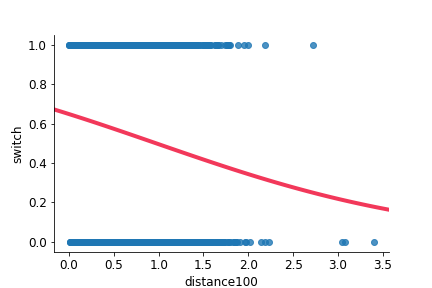
Logistic model fit of distance100 and switch.

Generalized Linear Models in Python

Linear vs logistic

LINEAR MODEL

glm('y ~ weight', 
    data = crab, 
    family = sm.families.Gaussian())

$\mu = -0.14 + \color{#B21AB4}{0.32}*weight$

For every one-unit increase in weight

  • $\text{\color{#B21AB4}{estimated probability}}$ increases by 0.32

LOGIT MODEL

glm('y ~ weight', 
    data = crab, 
    family = sm.families.Binomial())

$log(odds) = -3.69 + \color{#228FF5}{1.8}*weight$

For every one-unit increase in weight

  • $\text{\color{#228FF5}{log(odds)}}$ increase by 1.8
Generalized Linear Models in Python

Log odds interpretation

  • Logistic model $$ log(\frac{\mu}{1-\mu}) = \beta_0 + \beta_1x_1 $$

  • Increase $x$ by one-unit $$ log(\frac{\mu}{1-\mu}) = \beta_0 + \beta_1\color{blue}{(x_1+1)} $$

Generalized Linear Models in Python

Log odds interpretation

  • Logistic model $$ log(\frac{\mu}{1-\mu}) = \beta_0 + \beta_1x_1 $$

  • Increase $x$ by one-unit $$ log(\frac{\mu}{1-\mu}) = \beta_0 + \beta_1\color{blue}{(x_1+1)} = \beta_0 + \color{blue}{\beta_1x_1+\beta_1} $$

  • Take the exponential $$ (\frac{\mu}{1-\mu}) = \color{red}{\exp(\beta_0 + \beta_1x_1)}\color{blue}{\exp(\beta_1)} $$

Conclusion $\rightarrow$ the $\color{red}{\text{odds}}$ are multiplied by $\color{blue}{\exp(\beta_1)}$

Generalized Linear Models in Python

Log odds interpretation

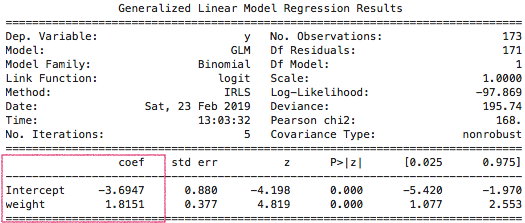
  • Crab model y ~ weight $$ log(\frac{\mu}{1-\mu}) = -3.6947 + \color{blue}{1.815}*weight $$

  • The odds of satellite crab multiply by $\color{blue}{\exp(1.815) = 6.14}$ for a unit increase in weight

Generalized Linear Models in Python

Log odds interpretation

  • Crab model y ~ weight $$ log(\frac{\mu}{1-\mu}) = \color{blue}{-3.6947} + 1.8151*weight $$

  • The odds of satellite crab multiply by $\exp(1.8151) = 6.14$ for a unit increase in weight

  • The intercept coefficient of $\color{blue}{-3.6947}$ denotes the baseline log odds
    • $\color{blue}{\exp(-3.6947)=0.0248}$ are the odds when $weight = 0$.
Generalized Linear Models in Python

Probability vs logistic fit

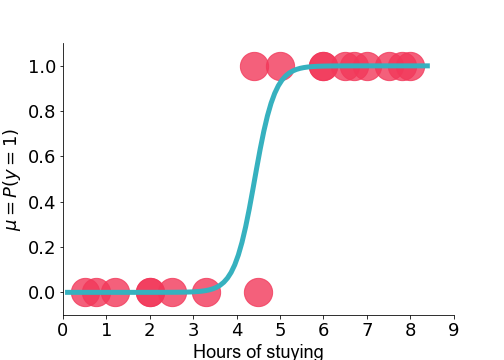
Logistic fit on the scatterplot of hours of studying and pass/fail the test.

Generalized Linear Models in Python

Probability vs logistic fit

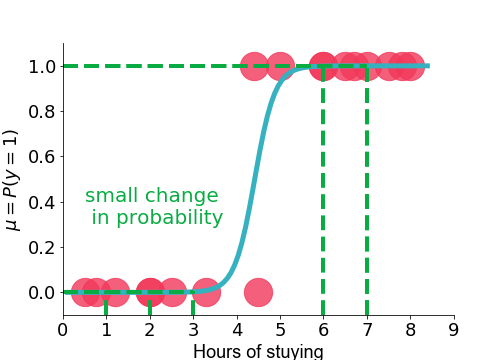
Indication of a small change in probability given the logistic fit and the value of the explanatory variable.

Generalized Linear Models in Python

Probability vs logistic fit

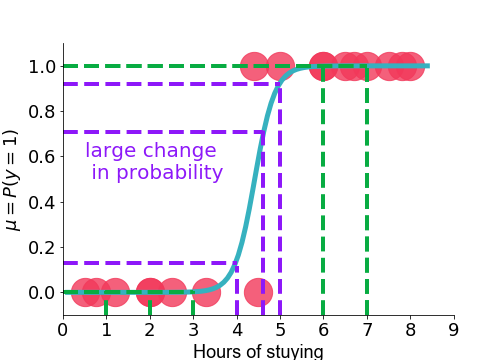
Indication of a large change in probability given the logistic fit and the value of the explanatory variable.

  • slope $\rightarrow \beta \times \mu(1-\mu)$
Generalized Linear Models in Python

Probability vs logistic fit

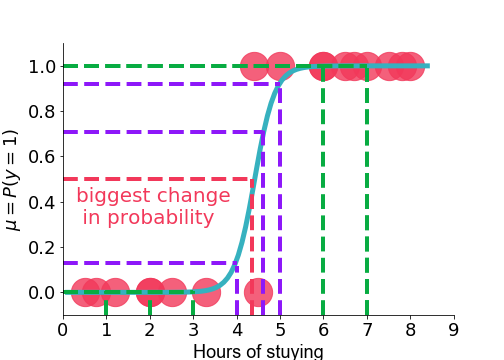
Indication of the biggest change in probability given the logistic fit and the value of the explanatory variable.

  • slope $\rightarrow \beta \times \mu(1-\mu)$
Generalized Linear Models in Python

Compute change in estimated probability

# Choose x (weight) and extract model coefficients
x = 1.5
intercept, slope = model_GLM.params

# Compute estimated probability
est_prob = np.exp(intercept + slope * x)/(1 + np.exp(intercept + slope * x))

0.2744

# Compute incremental change in estimated probability given x
ic_prob = slope * est_prob * (1 - est_prob)

0.3614
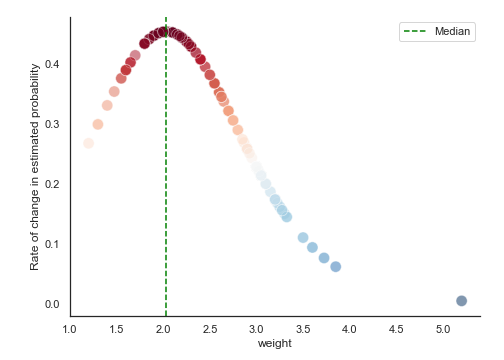
Generalized Linear Models in Python

Rate of change in probability for every x

$logit = -3.6947 + 1.8151*weight$

Generalized Linear Models in Python

Let's practice!

Generalized Linear Models in Python

Preparing Video For Download...