Interpreting model inference
Generalized Linear Models in Python

Ita Cirovic Donev
Data Science Consultant
Estimation of beta coefficient
- Maximum likelihood estimation (MLE)
- Estimated coefficient, $\hat\beta$
- log-likelihood takes on the maximum value

Estimation of beta coefficient
- Iteratively reweighted least squares (IRLS)
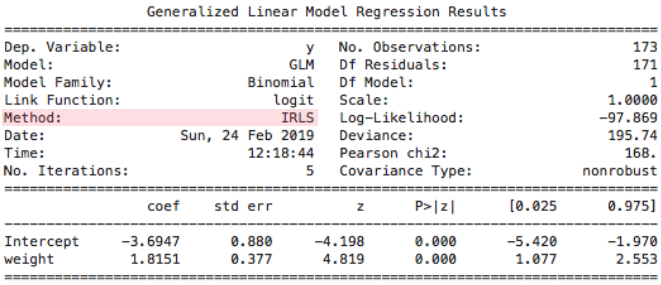
Significance testing
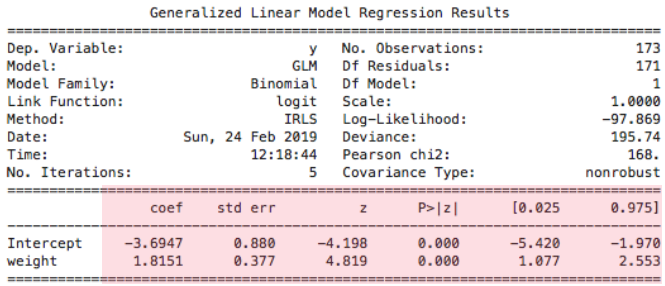
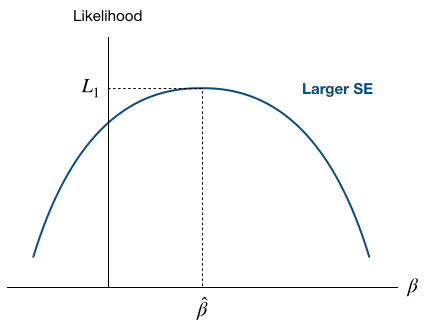
Standard error (SE)
- Flatter peak
$\rightarrow$ Location of maximum harder to define
$\rightarrow$ Larger SE
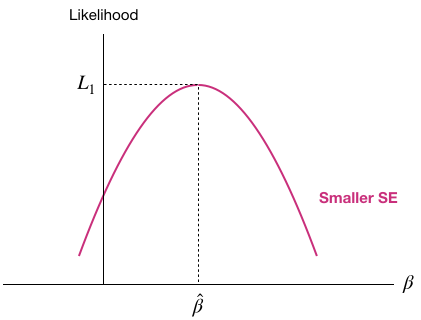
- Sharper peak
$\rightarrow$ Location of maximum more clearly defined
$\rightarrow$ Smaller SE
Computation of the standard error
# Extract variance-covariance matrix
print(model_GLM.cov_params())
Intercept weight
Intercept 0.774762 -0.325087
weight -0.325087 0.141903
# Compute standard error for weight
std_error = np.sqrt(0.141903)
0.3767
Variance-covariance matrix
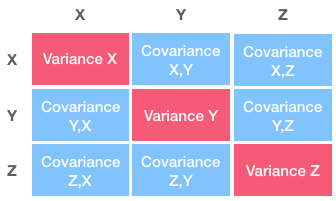
Significance testing
z-statistic $$ \color{#2485F2}{z=\hat\beta/SE} $$
$\color{#2485F2}{z}$ large $\Rightarrow$ coefficient $\ne0$ $\Rightarrow$ variable significant
- Rule of thumb: cut-off value of 2
Example: horseshoe crab modely ~ weight
$z = 1.8151/0.377 = 4.819$
Confidence intervals for beta
- Uncertainty of the estimates
- 95% confidence intervals for $\beta$
$$ [\color{#5A5AF3}{lower},\color{#D8498E}{upper}] $$
$$ [\color{#5A5AF3}{\hat\beta - 1.96 \times SE},\color{#D8498E}{\hat\beta+1.96 \times SE}] $$
Computing confidence intervals
Example: horseshoe crab model
coef std err
<hr />-------------------------------
Intercept -3.6947 0.880
weight 1.8151 0.377

Extract confidence intervals
print(model_GLM.conf_int())
0 1
Intercept -5.419897 -1.969555
weight 1.076826 2.553463
Extract confidence intervals
print(model_GLM.conf_int())
lower 1
Intercept -5.419897 -1.969555
weight 1.076826 2.553463
Extract confidence intervals
print(model_GLM.conf_int())
0 upper
Intercept -5.419897 -1.969555
weight 1.076826 2.553463
Confidence intervals for odds
Extract confidence intervals for $\beta$
Exponentiate endpoints
print(np.exp(model_GLM.conf_int()))
0 1
Intercept 0.004428 0.139519
weight 2.935348 12.851533
Let's practice!
Generalized Linear Models in Python


