Probability distributions and stories: The Binomial distribution

Statistical Thinking in Python (Part 1)

Justin Bois

Teaching Professor at the California Institute of Technology

Probability mass function (PMF)

The set of probabilities of discrete outcomes

Discrete Uniform PMF

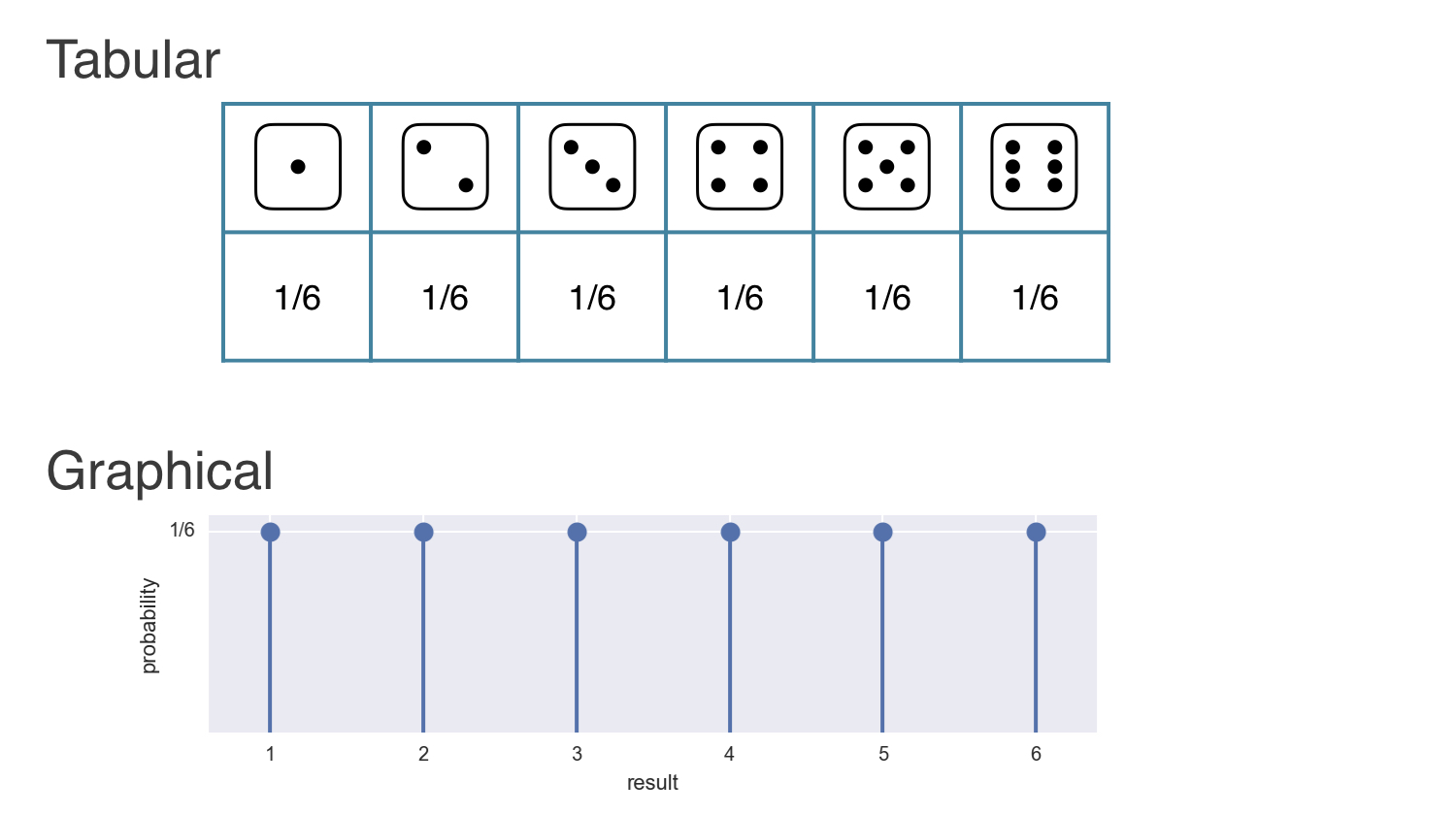
ch3-3.004.png

Probability distribution

A mathematical description of outcomes

Discrete Uniform distribution: the story

The outcome of rolling a single fair die is

Discrete
Uniformly distributed.

Binomial distribution: the story

The number r of successes in n Bernoulli trials with probability p of success, is Binomially distributed
The number r of heads in 4 coin flips with probability 0.5 of heads, is Binomially distributed

Sampling from the Binomial distribution

rng.binomial(4, 0.5)

rng.binomial(4, 0.5, size=10)

array([4, 3, 2, 1, 1, 0, 3, 2, 3, 0])

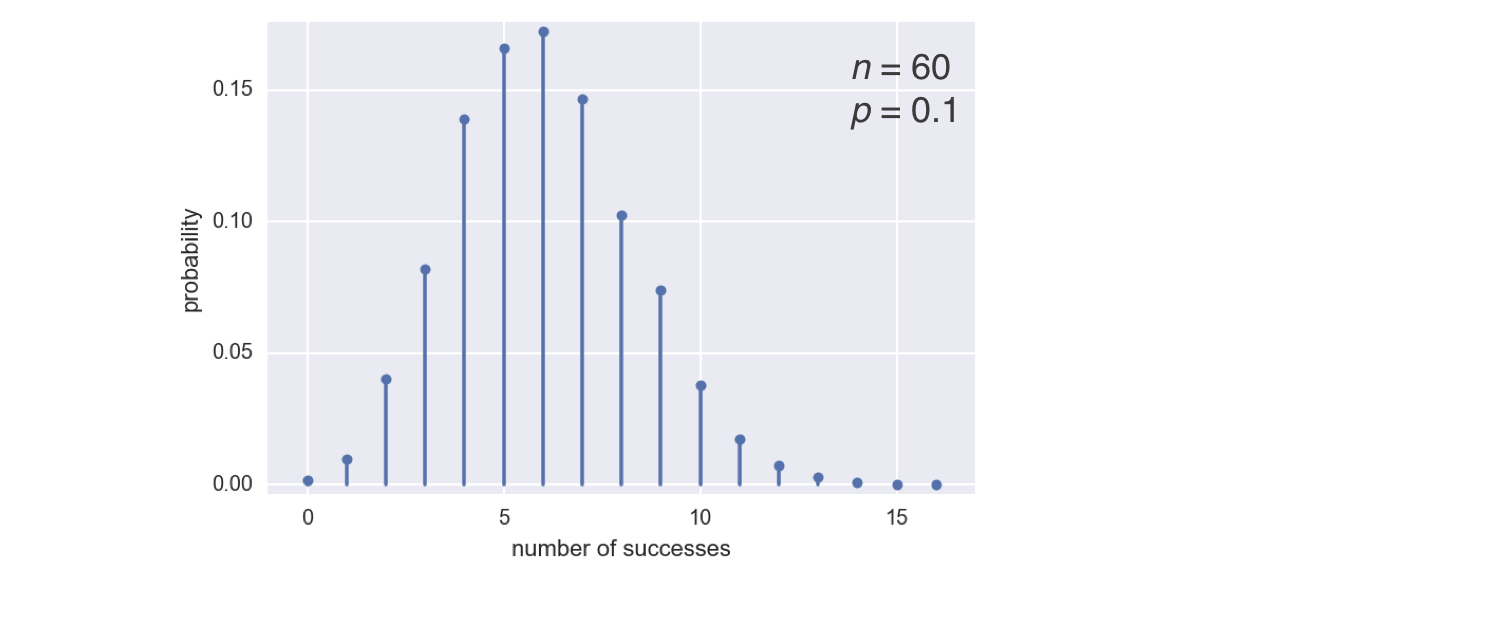
The Binomial PMF

samples = rng.binomial(60, 0.1, size=10000)
n = 60
p = 0.1

ch3-3.019.png

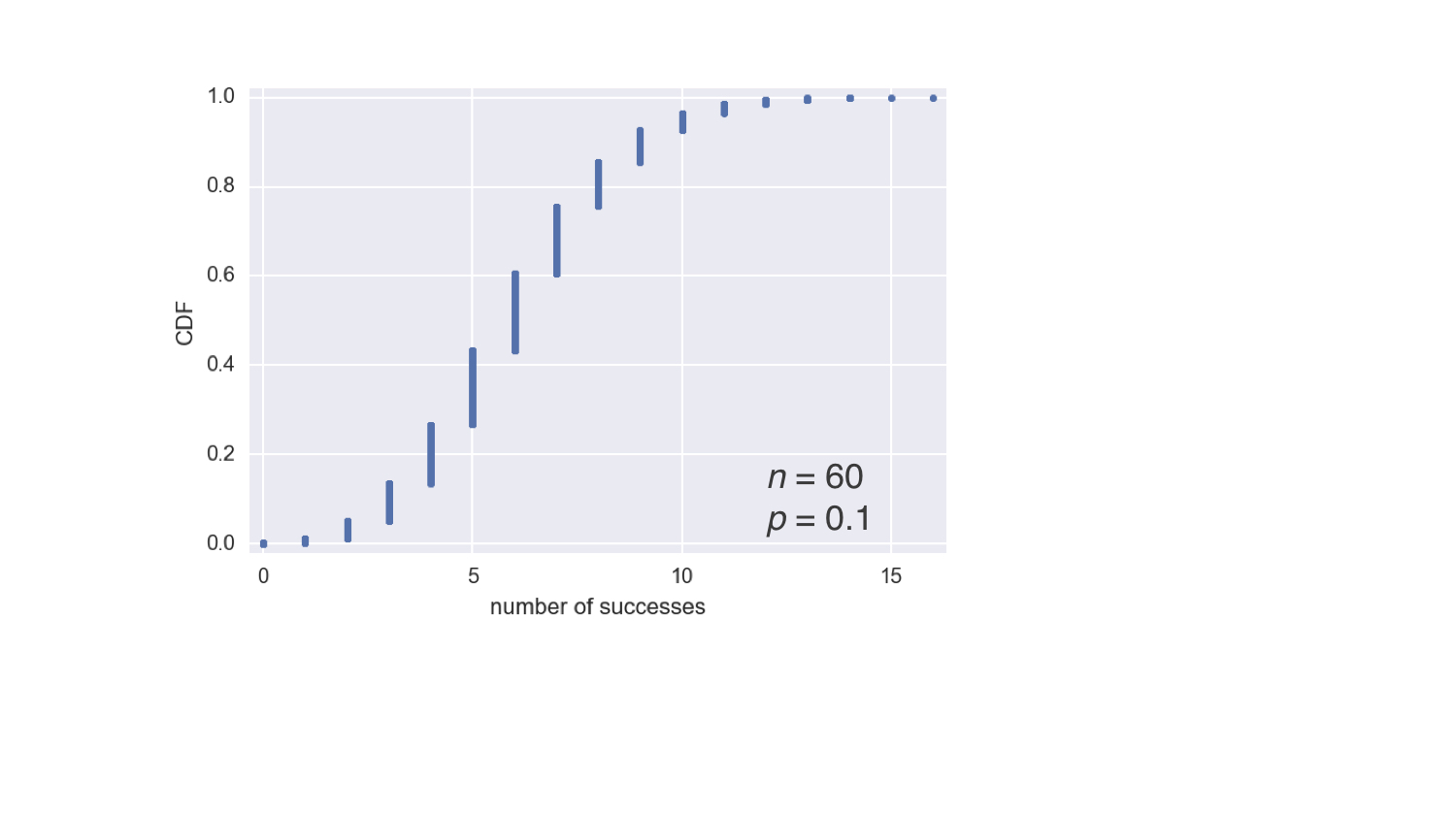
The Binomial CDF

import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
x, y = ecdf(samples)
_ = plt.plot(x, y, marker='.', linestyle='none')
plt.margins(0.02)
_ = plt.xlabel('number of successes')
_ = plt.ylabel('CDF')
plt.show()

The Binomial CDF

ch3-3.022.png

Let's practice!

Statistical Thinking in Python (Part 1)