Bootstrap confidence intervals

Statistical Thinking in Python (Part 2)

Justin Bois

Lecturer at the California Institute of Technology

Bootstrap replicate function

def bootstrap_replicate_1d(data, func):
    """Generate bootstrap replicate of 1D data."""
    bs_sample = np.random.choice(data, len(data))
    return func(bs_sample)

bootstrap_replicate_1d(michelson_speed_of_light, np.mean)

299859.20000000001

bootstrap_replicate_1d(michelson_speed_of_light, np.mean)

299855.70000000001

bootstrap_replicate_1d(michelson_speed_of_light, np.mean)

299850.29999999999

Many bootstrap replicates

bs_replicates = np.empty(10000)

for i in range(10000):
    bs_replicates[i] = bootstrap_replicate_1d(
                  michelson_speed_of_light, np.mean)

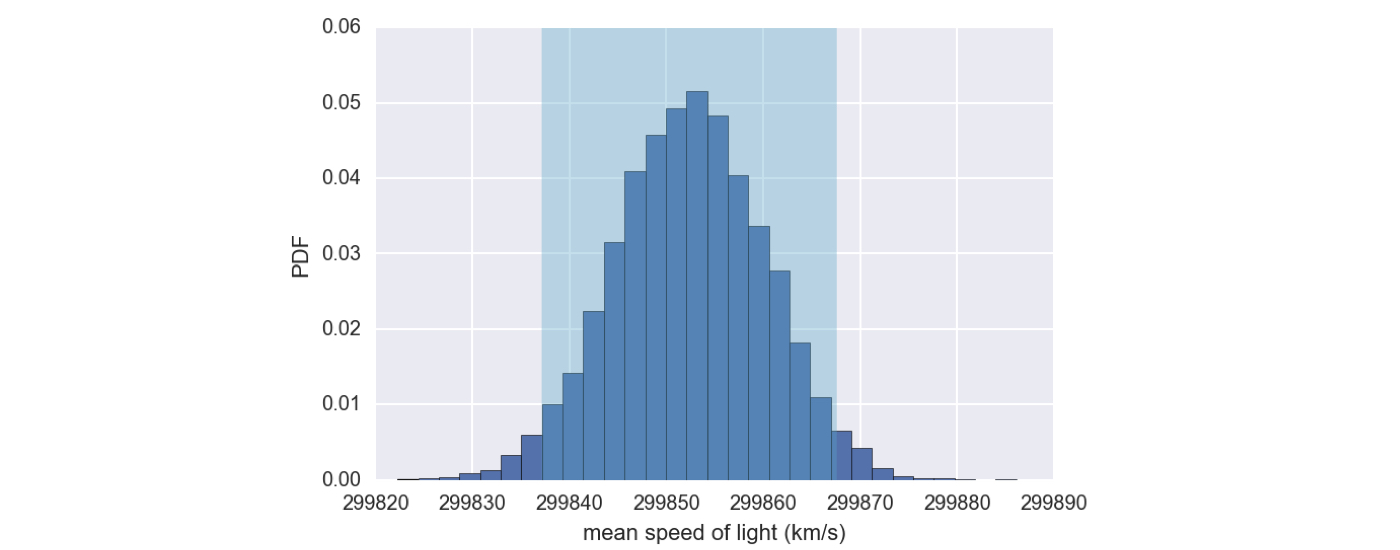
Plotting a histogram of bootstrap replicates

_ = plt.hist(bs_replicates, bins=30, normed=True)
_ = plt.xlabel('mean speed of light (km/s)')
_ = plt.ylabel('PDF')
plt.show()

Bootstrap estimate of the mean

ch2-2.011.png

Confidence interval of a statistic

If we repeated measurements over and over again, p% of the observed values would lie within the p% confidence interval.

Bootstrap confidence interval

conf_int = np.percentile(bs_replicates, [2.5, 97.5])

array([ 299837.,  299868.])

ch2-2.016.png

Let's practice!

Statistical Thinking in Python (Part 2)