What is recursion?

Practicing Coding Interview Questions in Python

Kirill Smirnov

Data Science Consultant, Altran

Definition

Recursion is the process of defining a problem in terms of itself
Recursion is a process in which a function calls itself as a subroutine

Example: Factorial $n!$

$n! = n\cdot(n-1)\cdot(n-2)\cdot...\cdot1$

$n = 4$:

$4! = 4\cdot3\cdot2\cdot1$

4! = 24

Factorial - Iterative Approach

$n! = n\cdot(n-1)\cdot(n-2)\cdot...\cdot1 = $

$ = 1\cdot2\cdot3\cdot...\cdot n$

Iterative solution:

# iterative factorial
def fact_iter(n):
    result = 1
    # looping over numbers from 1 to n
    for num in range(1, n+1)
        result = num * result

    return result

$n = 4:$

result = 1

result = 1 * result(1) = 1
result = 2 * result(1) = 2
result = 3 * result(2) = 6
result = 4 * result(4) = 24

$4! = 1 \cdot 2 \cdot 3 \cdot 4 = 24$

Factorial - Recursive Approach

$n!$ $=n\cdot(n-1)!$

def fact_rec(n):
    return n * fact_rec(n-1)

What's wrong with that code?

fact_rec(4)

RecursionError

We must define a base case!

$n! = n\cdot(n-1)\cdot(n-2)\cdot...\cdot1$

A stopping criterion / base case: $1! = 1$

def fact_rec(n):
    if n == 1:
        return 1
    return n * fact_rec(n-1)

fact_rec(4)

Wrapping Up

Recursive functions have two main components:

a recursive call to a smaller problem of itself
a base case that prevents an infinite calling

Example - Decision Trees

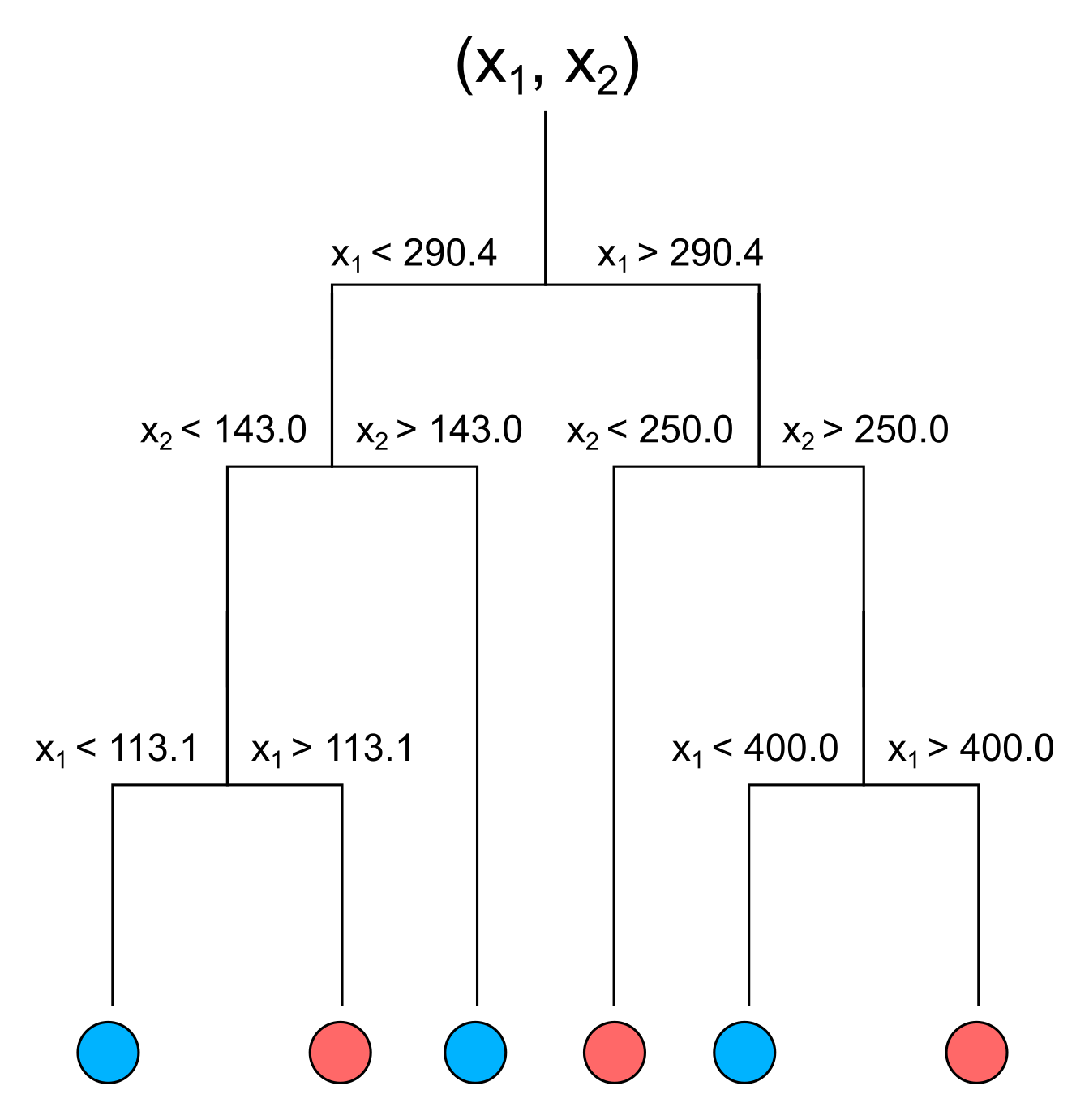
Decision Tree

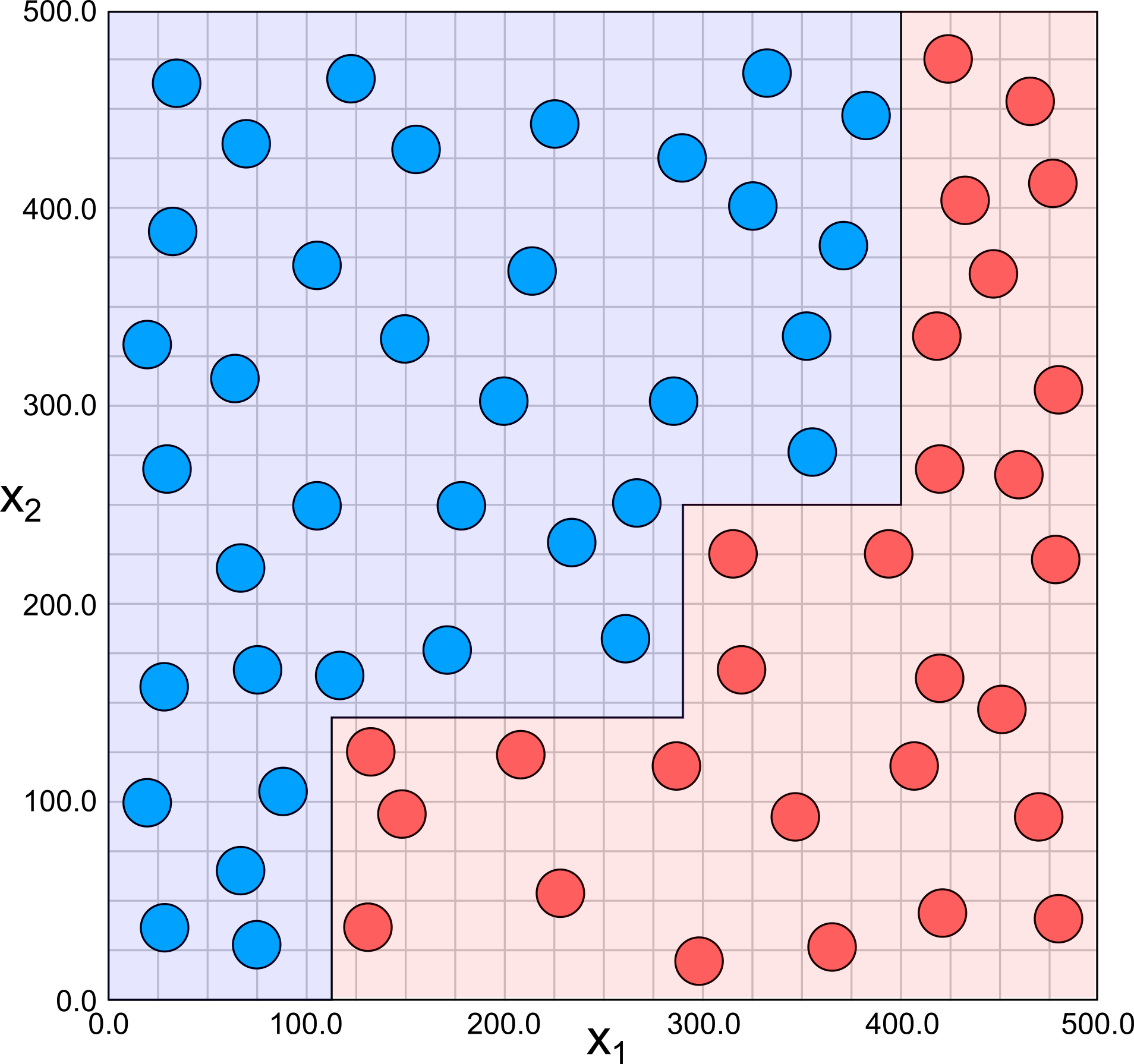
Classification using the decision tree

Traversing a Decision Tree

Traversing the decision tree

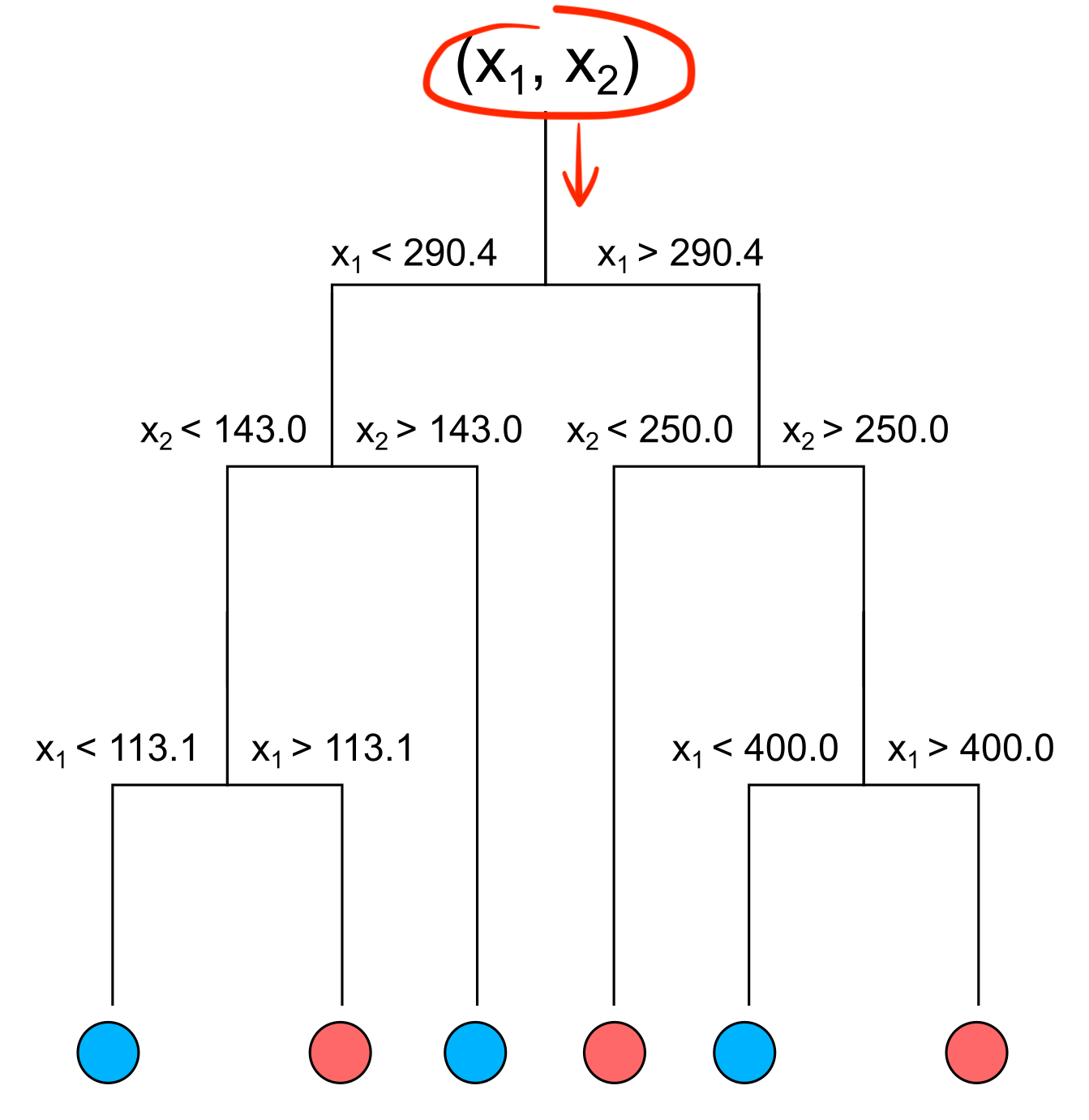
x - a new sample $(x_1, x_2)$

# Pseudo algorithm for finding out the category:

category = pred(node, x):

  # Check if there is a split  
  if node.hasSplitting:

    # Check which child node to take
    if node.goToLeftChild(x):
      return pred(node.leftChild, x)   
    if node.goToRightChild(x):
      return pred(node.rightChild, x)

Traversing a Decision Tree

Prediction using the decision tree

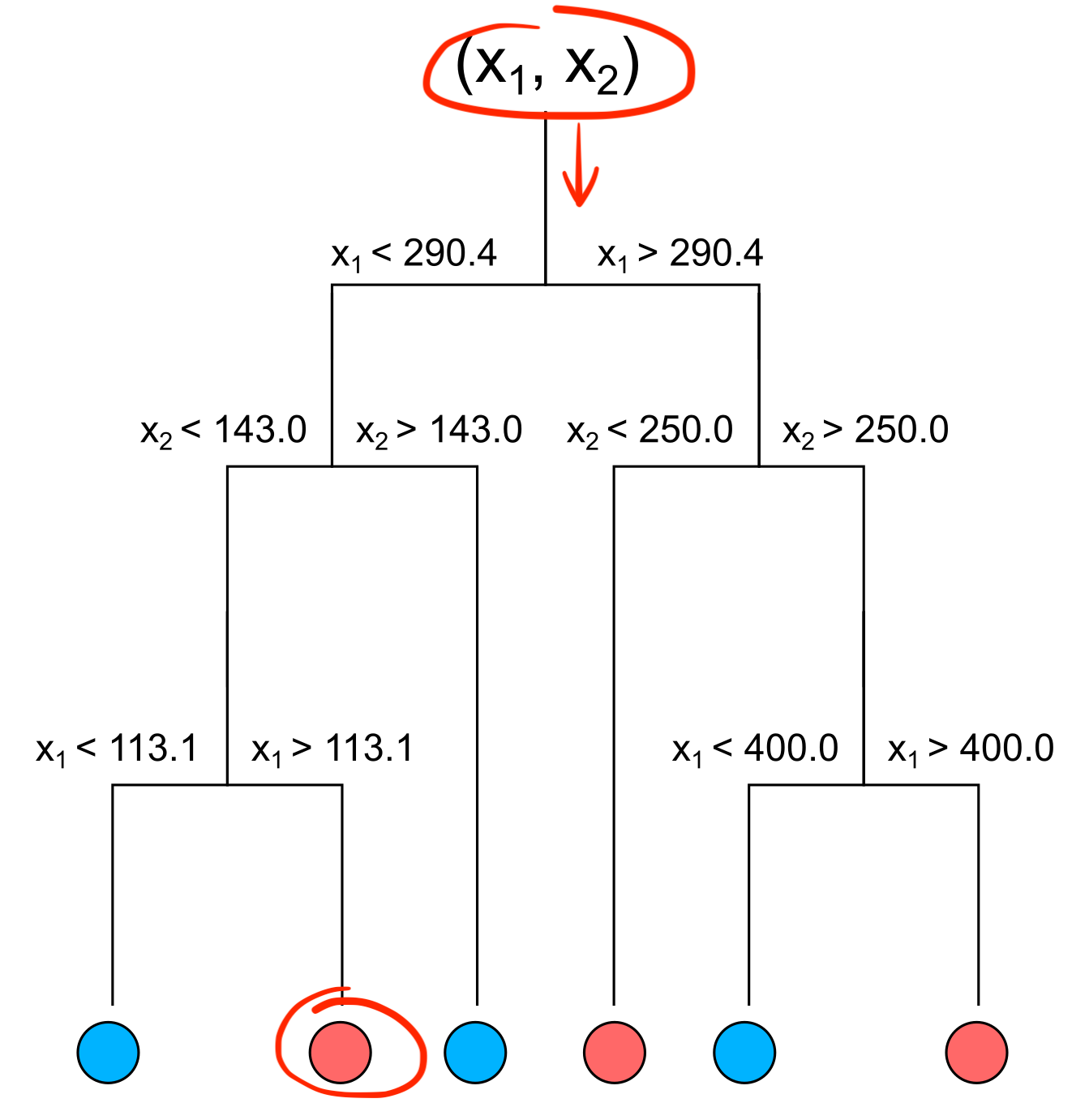
x - a new sample $(x_1, x_2)$

# Pseudo algorithm for finding out the category:

category = pred(node, x):

  # Check if there is a split  
  if node.hasSplitting:

    # Check which child node to take
    if node.goToLeftChild(x):
      return pred(node.leftChild, x) 
    if node.goToRightChild(x):
      return pred(node.rightChild, x)

  # Returning the category
  return node.category

Let's practice!

Practicing Coding Interview Questions in Python