Type I errors

Performing Experiments in Python

Luke Hayden

Instructor

Ways of being wrong

When we run a test:

Real effect present No real effect present
Effect found (positive : alternative hypothesis) True Positive False Positive
No effect found (negative: null hypothesis) False Negative True Negative

 

Type I error : find difference where none exists

 

Type II error : fail to find difference that does exist

Performing Experiments in Python

Avoiding type I errors

Basis of tests

  • Statistical tests are probabilistic

  • Quantify likelihood of results under null hypothesis

 

Consider:

  • Significant results are improbable, not impossible under null hypothesis

  • Still possible result are by chance

Performing Experiments in Python

Picking a single result can be misleading

Example

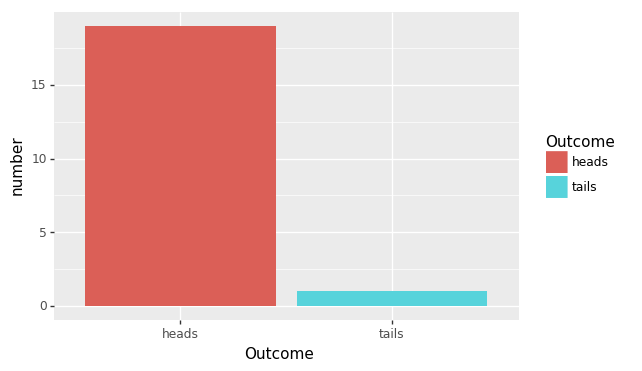
Results of flipping a single coin

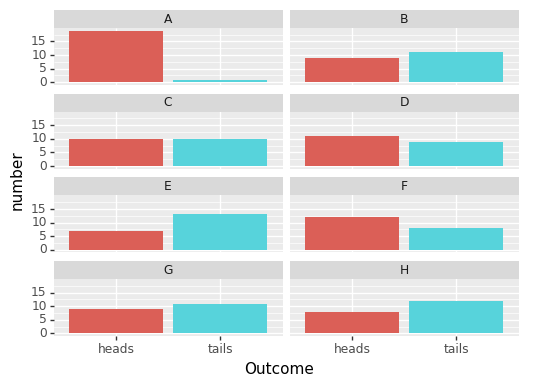
Results of flipping eight coins

Performing Experiments in Python

Accounting for multiple tests

By design

  • Avoid "p-value fishing"

By correction

  • Correct p-values for presence of multiple tests

Correction methods

  • Bonferroni and Šídák

  • Choose method based on independence of tests

Performing Experiments in Python

Bonferroni correction

  • Conservative method

  • Simple

 

Use when

  • Tests are not independent from each other
import statsmodels as sm
from scipy import stats

t_1= stats.ttest_ind(Array1, Array2)
t_2= stats.ttest_ind(Array2, Array3)
t_3= stats.ttest_ind(Array1, Array3)

pvals_array = [t_1[1],t_2[1],t_3[1]]

adjustedvalues=  sm.stats.multitest.multipletests(
pvals_array, alpha=0.05, method='b')
Performing Experiments in Python

Bonferroni correction example

  • Multiple non-independent t-tests

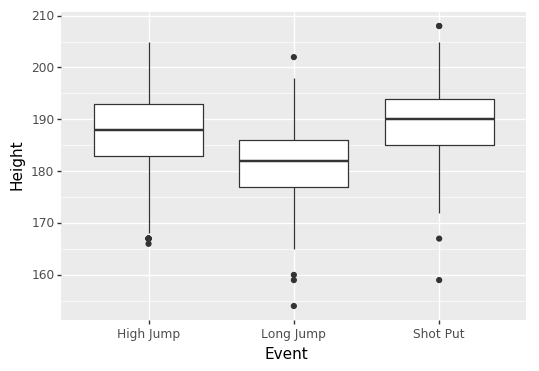
Boxplots of athlete heights for three Olympic events

Performing Experiments in Python
from scipy import stats
import statsmodels as sm

t_result_1= stats.ttest_ind(HighJumpVals, LongJumpVals)
t_result_2= stats.ttest_ind(LongJumpVals, ShotPutVals)
t_result_3= stats.ttest_ind(HighJumpVals, HighJumpVals)

pvals_array = [t_result_1[1],t_result_2[1],t_result_3[1]]
adjustedvalues=  sm.stats.multitest.multipletests(pvals_array, alpha=0.05, method='b')
print(adjustedvalues)

(array([ True,  True, False]), 
array([6.72030836e-63, 3.46967459e-97, 1.00000000e+00]), 
0.016952427508441503, 0.016666666666666666)
Performing Experiments in Python

Šídák correction

  • Less conservative method

 

Use when

  • Tests are independent from each other
import statsmodels as sm

t_1= stats.ttest_ind(Array1, Array2)
t_2= stats.ttest_ind(Array3, Array4)
t_3= stats.ttest_ind(Array5, Array6)

pvals_array = [t_1[1],t_2[1],t_3[1]]

adjustedvalues=  sm.stats.multitest.multipletests(
pvals_array, alpha=0.05, method='s')
Performing Experiments in Python

Šídák correction example

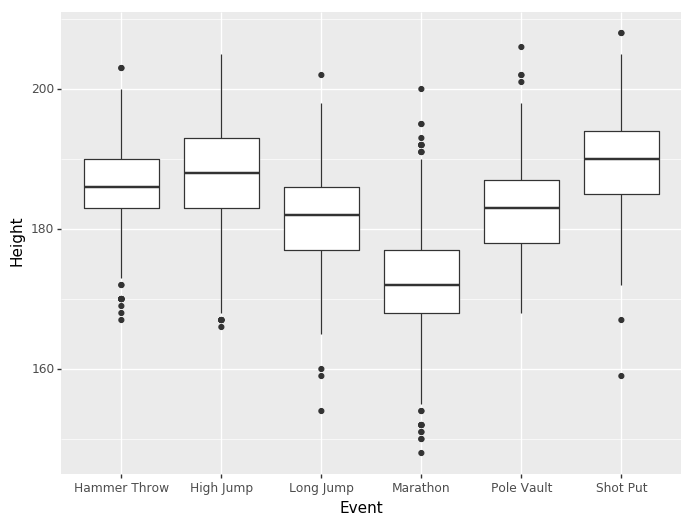
Boxplots of athlete heights for six Olympic events

Performing Experiments in Python
from scipy import stats
import statsmodels as sm

t_result_1 = stats.ttest_ind(HighJumpVals, LongJumpVals)
t_result_2 = stats.ttest_ind(ShotPutVals, HammerVals)
t_result_3 = stats.ttest_ind(MarathonVals, PoleVals)

pvals_array = [t_result_1[1],t_result_2[1],t_result_3[1]]
adjustedvaluesm = sm.stats.multitest.multipletests(pvals_array, alpha=0.05, method='s')
print(adjustedvalues)

(array([ True,  True,  True]), array([0., 0., 0.]),
0.016952427508441503, 0.016666666666666666)
Performing Experiments in Python

Let's practice!

Performing Experiments in Python

Preparing Video For Download...