Cosine similarity

Feature Engineering for NLP in Python

Rounak Banik

Data Scientist

Cosine similarity

¹ Image courtesy techninpink.com

The dot product

Consider two vectors,

$$V = (v_1, v_2, \cdots, v_n), W = (w_1, w_2, \cdots, w_n)$$

Then the dot product of V and W is,

$$V \cdot W = (v_1 \times w_1) + (v_2 \times w_2) + \cdots + (v_n \times w_n) $$

Example:

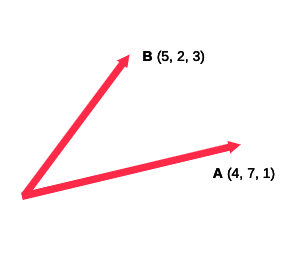
$$A = (4, 7, 1) \; , \; B = (5, 2, 3)$$

$$A \cdot B = (4 \times 5) + (7 \times 2) + \cdots (1 \times 3)$$

$$= 20 + 14 + 3 = 37 \color{white}{A \cdot B d}$$

$$$$

Magnitude of a vector

For any vector,

$$V = (v_1, v_2, \cdots, v_n)$$

The magnitude is defined as,

$$||\mathbf{V}|| = \sqrt{(v_1)^{2} + (v_2)^{2} + ... + (v_n)^{2}} $$

Example:

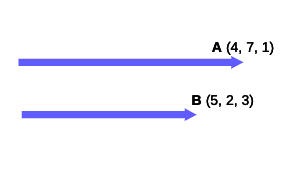
$$A = (4, 7, 1) \; , \; B = (5, 2, 3)$$

$$||\mathbf{A}|| = \sqrt{(4)^{2} + (7)^{2} + (1)^{2}} $$

$$ \color{white}{filler} = \sqrt{16 + 49 + 1} = \sqrt{66}$$

The cosine score

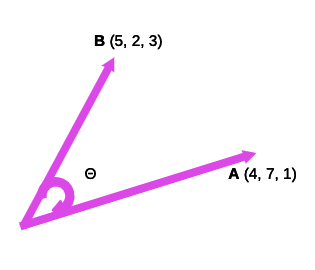
Angle between vectors A and B

$$A: (4, 7, 1)$$

$$B: (5, 2, 3)$$

The cosine score,

$$cos(A,B) = \frac{A \cdot B}{|A| \cdot |B|}$$

$$\color{white}{fillers lorem}= \frac{37}{\sqrt{66} \times \sqrt{38}}$$

$$\color{white}{fillers l}= 0.7388$$

Cosine Score: points to remember

Value between -1 and 1.
In NLP, value between 0 and 1.
Robust to document length.

Implementation using scikit-learn

# Import the cosine_similarity
from sklearn.metrics.pairwise import cosine_similarity

# Define two 3-dimensional vectors A and B
A = (4,7,1)
B = (5,2,3)

# Compute the cosine score of A and B
score = cosine_similarity([A], [B])

# Print the cosine score
print(score)

array([[ 0.73881883]])

Let's practice!

Feature Engineering for NLP in Python