Convexity

Bond Valuation and Analysis in R

Clifford Ang

Senior Vice President, Compass Lexecon

Convexity measure

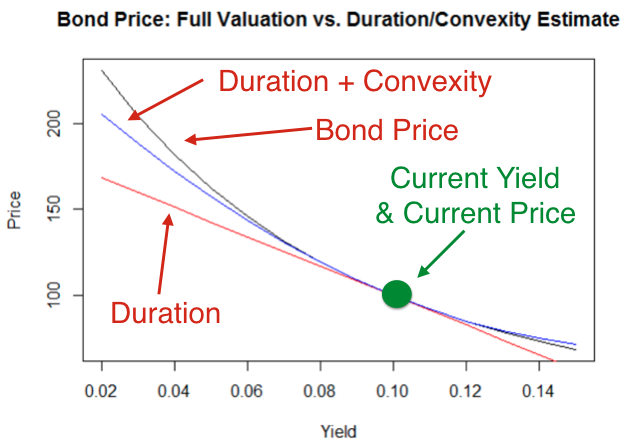
  • Duration does a poor job when yield changes are large
  • Convexity measure is used to adjust the duration estimate
Bond Valuation and Analysis in R

Calculating the convexity measure

$$

$$ C = \frac{P(down)+P(up)-2 \cdot P}{(P \cdot (\Delta y)^2} $$

  • $C$ = Convexity measure
  • $P(down)$ = Price when yield goes down
  • $P(up)$ = Price when yield goes up
  • $P$ = Current price
  • $(\Delta y)^2$ = Change in yield squared
  • $2 \cdot P$ = 2x current price
Bond Valuation and Analysis in R

Estimating effect on price

$$\frac{\Delta P}{P} = 0.5 \cdot C \cdot (\Delta y)^2$$

  • $\frac{\Delta P}{P}$ = Percent change

$$\Delta P = 0.5 \cdot C \cdot (\Delta y)^2 \cdot P$$

  • $\Delta P$ = Dollar change
  • $C$ = Convexity measure
  • $(\Delta y)^2$ = Change in yield squared
  • $P$ = Current price
Bond Valuation and Analysis in R

How do you use these formulas?

  • Example (same as duration)
    • $100 par value, 5% coupon rate, 10 years to maturity, initial yield = 4%, expected increase in yield = 1%
p

108.1109

(convexity <- (p_down + p_up - 2 * p) / (p * (0.01^2)))

77.56981
Bond Valuation and Analysis in R

How do you use these formulas?

(convexity_pct_change <- 0.5 * convexity * 0.01 ^ 2)

0.00387849

(convexity_dollar_change <- 0.5 * convexity * 0.01 ^ 2 * p)

0.4193071
Bond Valuation and Analysis in R

Effect of duration and convexity

  • Estimated change in price
duration_dollar_change

-8.530203

convexity_dollar_change

0.4193071
Bond Valuation and Analysis in R
duration_dollar_change + convexity_dollar_change

-8.110896
  • Estimated price
p

108.1109

duration_dollar_change + convexity_dollar_change + p

100
Bond Valuation and Analysis in R

Yield vs price

Bond Valuation and Analysis in R

Let's practice!

Bond Valuation and Analysis in R

Preparing Video For Download...