Fitting time series models
ARIMA Models in Python

James Fulton
Climate informatics researcher
Creating a model
from statsmodels.tsa.arima.model import ARIMA
# This is an ARMA(p,q) model
model = ARIMA(timeseries, order=(p,0,q))
Creating AR and MA models
ar_model = ARIMA(timeseries, order=(p,0,0))
ma_model = ARIMA(timeseries, order=(0,0,q))
Fitting the model and fit summary
model = ARIMA(timeseries, order=(2,0,1))results = model.fit()
print(results.summary())
Fit summary
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 1000
Model: ARMA(2, 1) Log Likelihood 148.580
Date: Thu, 25 Apr 2022 AIC -287.159
Time: 22:57:00 BIC -262.621
Sample: 0 HQIC -277.833
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0017 0.012 -0.147 0.883 -0.025 0.021
ar.L1.y 0.5253 0.054 9.807 0.000 0.420 0.630
ar.L2.y -0.2909 0.042 -6.850 0.000 -0.374 -0.208
ma.L1.y 0.3679 0.052 7.100 0.000 0.266 0.469
Fit summary
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 1000
Model: ARMA(2, 1) Log Likelihood 148.580
Date: Thu, 25 Apr 2022 AIC -287.159
Time: 22:57:00 BIC -262.621
Sample: 0 HQIC -277.833
Covariance Type: opg
Fit summary
============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ const -0.0017 0.012 -0.147 0.883 -0.025 0.021 ar.L1.y 0.5253 0.054 9.807 0.000 0.420 0.630 ar.L2.y -0.2909 0.042 -6.850 0.000 -0.374 -0.208 ma.L1.y 0.3679 0.052 7.100 0.000 0.266 0.469sigma2 1.6306 0.339 6.938 0.000 0.583 1.943
Introduction to ARMAX models
- Exogenous ARMA
Use external variables as well as time series
ARMAX = ARMA + linear regression
ARMAX equation
ARMA(1,1) model : $$y_t = a_1 y_{t-1} + m_1 \epsilon_{t-1} + \epsilon_t$$
ARMAX(1,1) model : $$y_t = x_1 z_t + a_1 y_{t-1} + m_1 \epsilon_{t-1} + \epsilon_t$$
ARMAX example
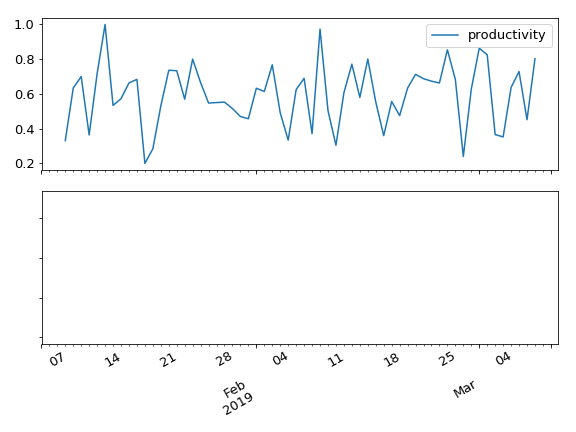
ARMAX example
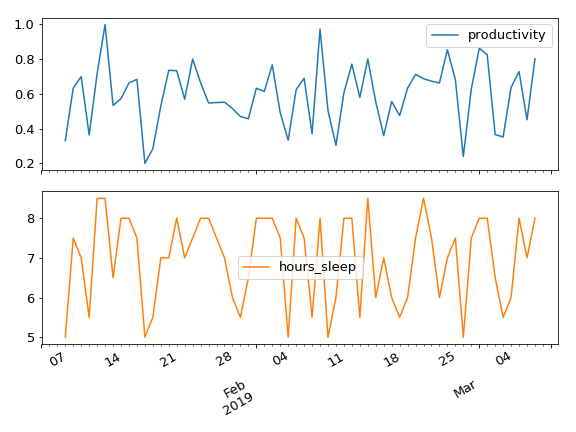
Fitting ARMAX
# Instantiate the model model = ARIMA(df['productivity'], order=(2,0,1), exog=df['hours_sleep'])# Fit the model results = model.fit()
ARMAX summary
==============================================================================
coef std err z P>|z| [0.025 0.975]
-----------------------------------------------------------------------------
const -0.1936 0.092 -2.098 0.041 -0.375 -0.013
x1 0.1131 0.013 8.602 0.000 0.087 0.139
ar.L1.y 0.1917 0.252 0.760 0.450 -0.302 0.686
ar.L2.y -0.3740 0.121 -3.079 0.003 -0.612 -0.136
ma.L1.y -0.0740 0.259 -0.286 0.776 -0.581 0.433
Let's practice!
ARIMA Models in Python

