Intro to AR, MA and ARMA models

ARIMA Models in Python

James Fulton

Climate informatics researcher

AR models

Autoregressive (AR) model

AR(1) model : $$y_t = a_1 y_{t-1} + \epsilon_t$$

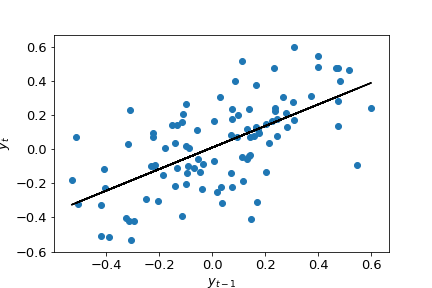
AR models

Autoregressive (AR) model

AR(1) model : $$y_t = a_1 y_{t-1} + \epsilon_t$$

AR(2) model : $$y_t = a_1 y_{t-1} + a_2 y_{t-2} + \epsilon_t$$

AR(p) model : $$y_t = a_1 y_{t-1} + a_2 y_{t-2} + ... + a_p y_{t-p} + \epsilon_t$$

MA models

Moving average (MA) model

MA(1) model : $$y_t = m_1 \epsilon_{t-1} + \epsilon_t$$

MA(2) model : $$y_t = m_1 \epsilon_{t-1} + m_2 \epsilon_{t-2} + \epsilon_t$$

MA(q) model : $$y_t = m_1 \epsilon_{t-1} + m_2 \epsilon_{t-2} + ... + m_q \epsilon_{t-q} + \epsilon_t$$

ARMA models

Autoregressive moving-average (ARMA) model

ARMA = AR + MA

ARMA(1,1) model : $$y_t = a_1 y_{t-1} + m_1 \epsilon_{t-1} + \epsilon_t$$

ARMA(p, q)

p is order of AR part
q is order of MA part

Creating ARMA data

$$y_t = a_1 y_{t-1} + m_1 \epsilon_{t-1} + \epsilon_t$$

Creating ARMA data

$$y_t = 0.5 y_{t-1} + 0.2 \epsilon_{t-1} + \epsilon_t$$

from statsmodels.tsa.arima_process import arma_generate_sample

ar_coefs = [1, -0.5]
ma_coefs = [1, 0.2]

y = arma_generate_sample(ar_coefs, ma_coefs, nsample=100, scale=0.5)

Creating ARMA data

$$y_t = 0.5 y_{t-1} + 0.2 \epsilon_{t-1} + \epsilon_t$$

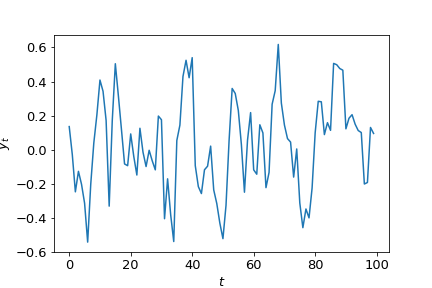
Fitting and ARMA model

from statsmodels.tsa.arima.model import ARIMA

# Instantiate model object
model = ARIMA(y, order=(1,0,1))

# Fit model
results = model.fit()

Let's practice!

ARIMA Models in Python