Distribution of statistics

Foundations of Inference in R

Jo Hardin

Instructor

Null statistic

Difference in proportions: $\hat{p} - p$
Ratio: $\dfrac{\hat{p}}{p}$
Interested in whether observed statistic is different from values obtained by shuffling

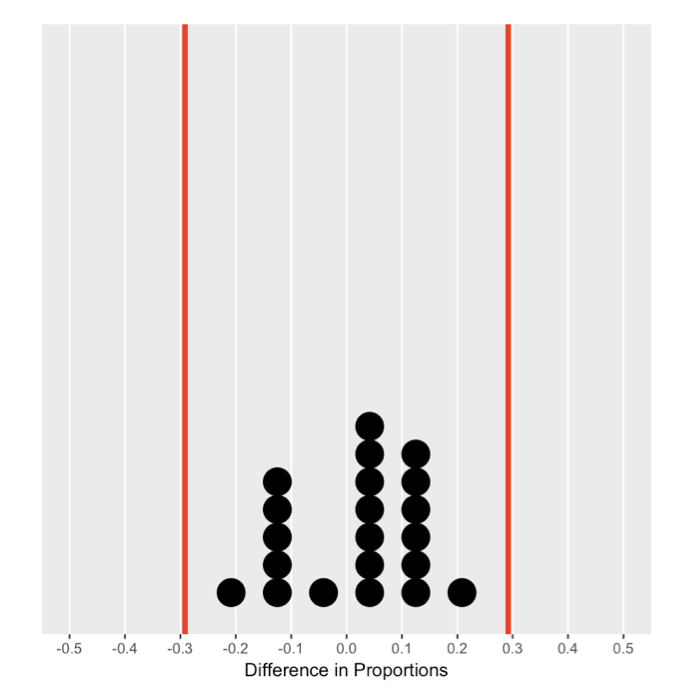
ch2_2_v5.007.png

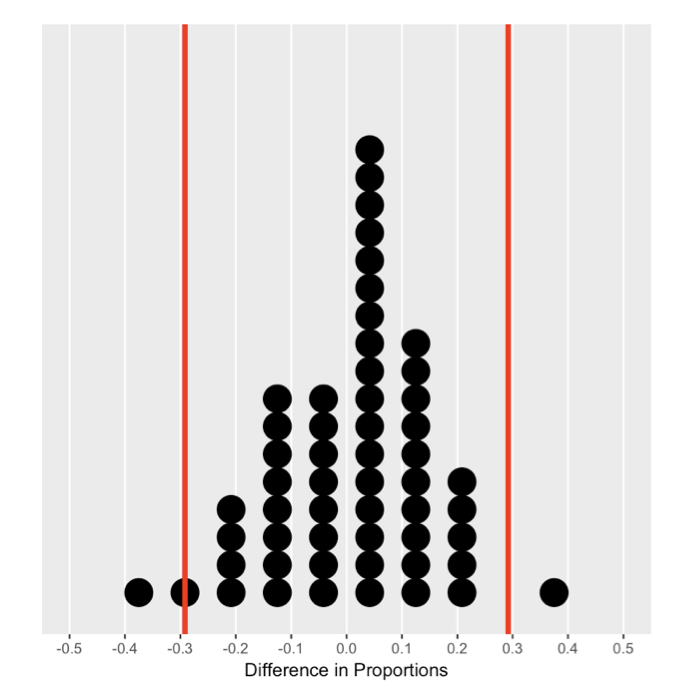
ch2_2_v5.008.png

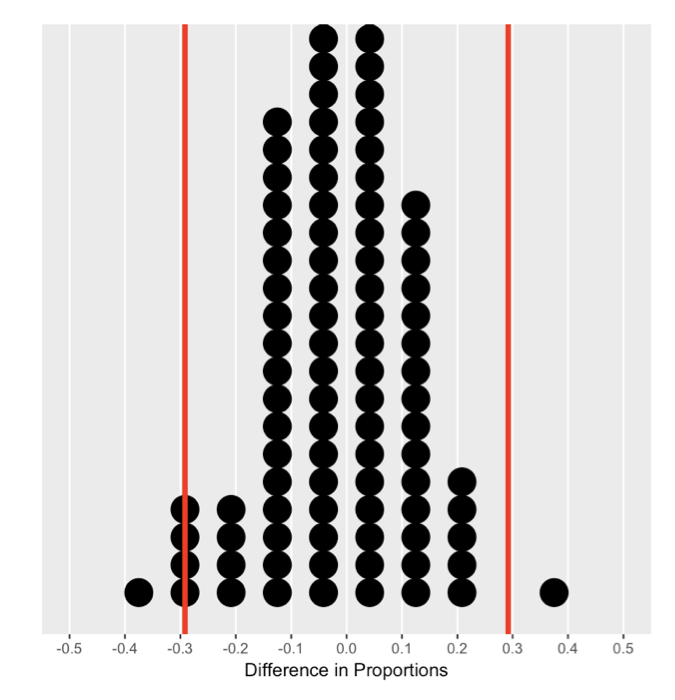
ch2_2_v5.009.png

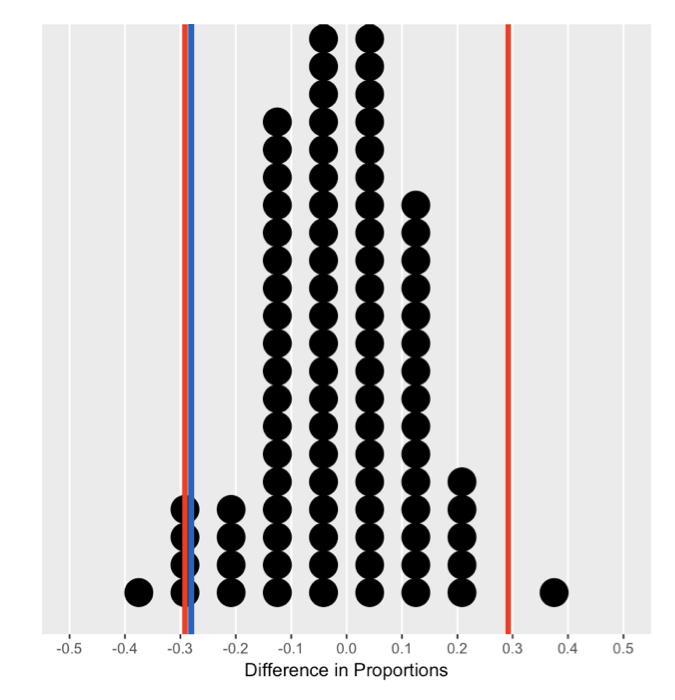
ch2_2_v5.010.png

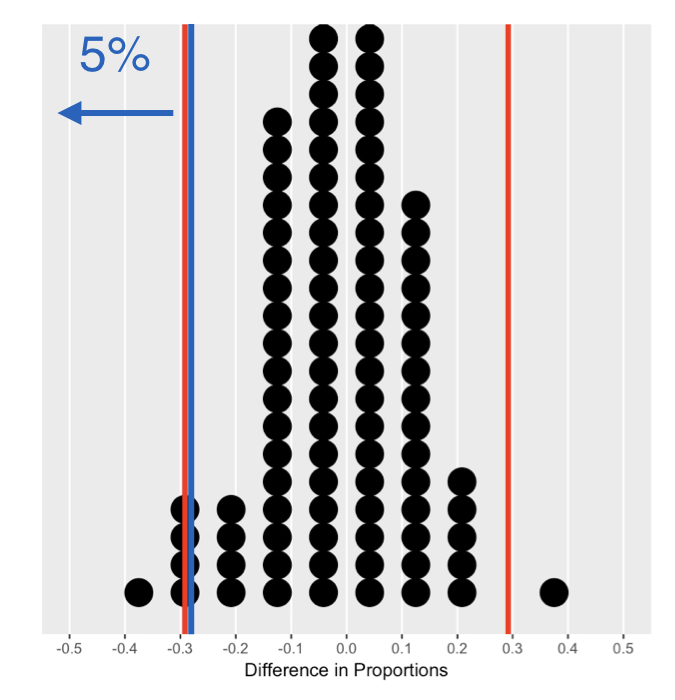
ch2_2_v5.011.png

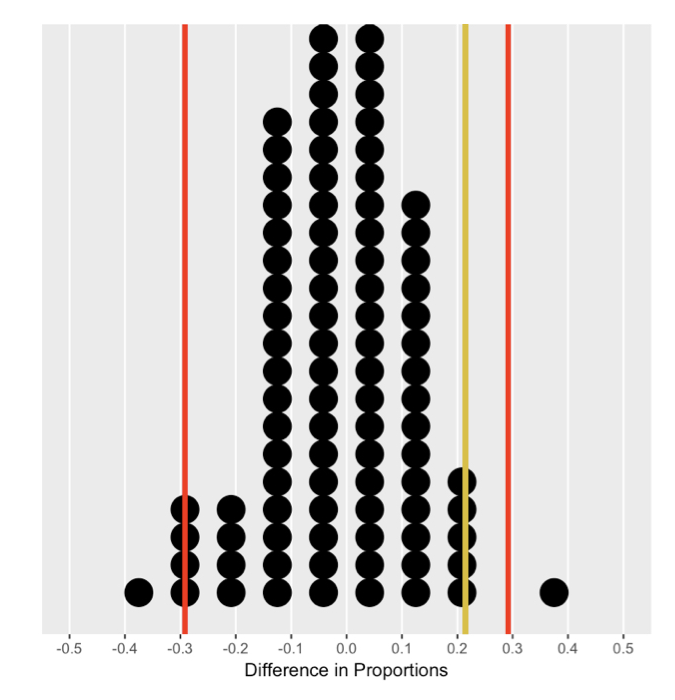
ch2_2_v5.012.png

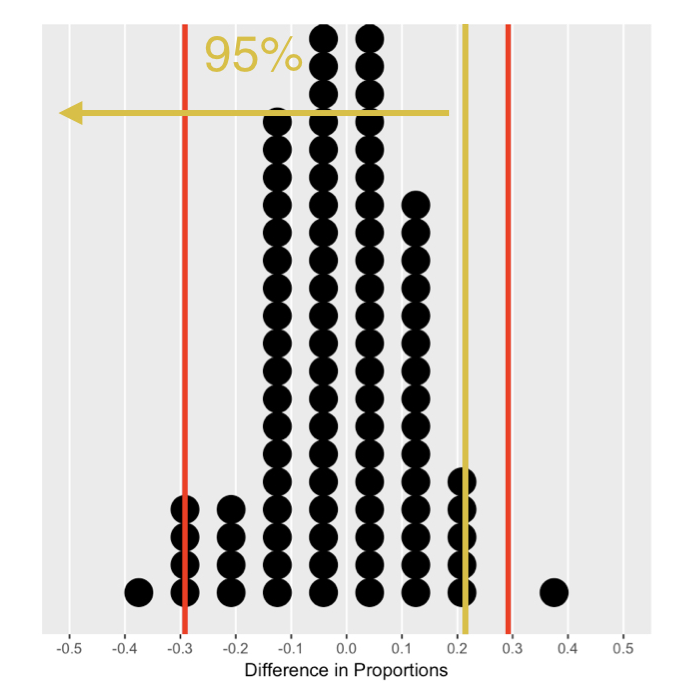
ch2_2_v5.013.png

 disc_perm %>% 
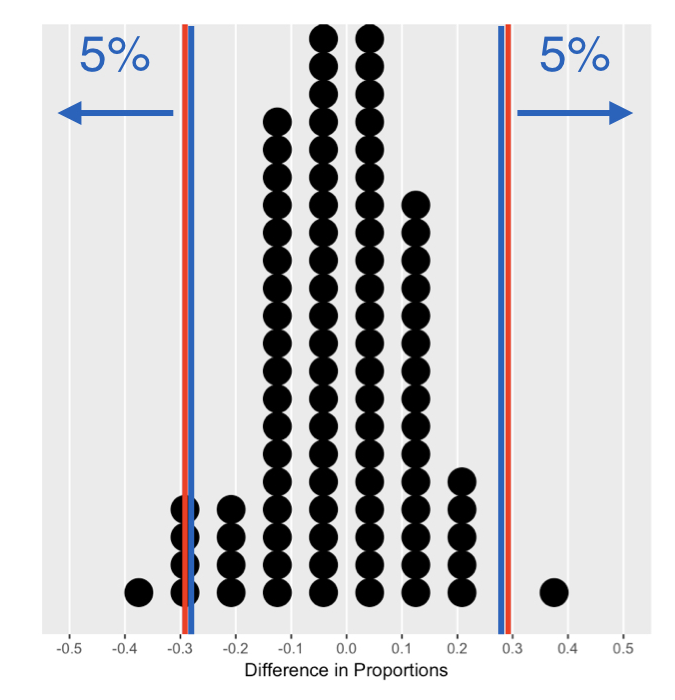
    summarize(q.05 = quantile(diff_perm, p = 0.05),
              q.95 = quantile(diff_perm, p = 0.95))

# A tibble: 1 × 2
       q.05      q.95 
       <dbl>     <dbl>
1 -0.2083333 0.2083333

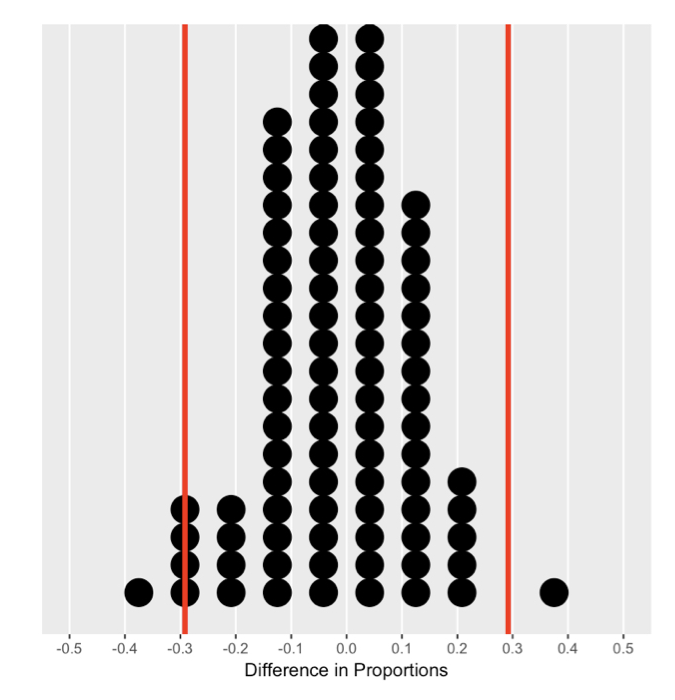
ch2_2_v5.019.png

ch2_2_v5.020.png

Foundations of Inference in R