Bootstrapping

Foundations of Inference in R

Jo Hardin

Instructor

Hypothesis testing

How do samples from the null population vary?
Statistic, proportion of successes in sample → $\hat{p}$
Parameter, proportion of successes in population → ${p}$

Confidence intervals

No null population, unlike in hypothesis testing
How do $p$ and $\hat{p}$ vary?

ch4_2_v4.012.png

ch4_2_v4.013.png

ch4_2_v4.014.png

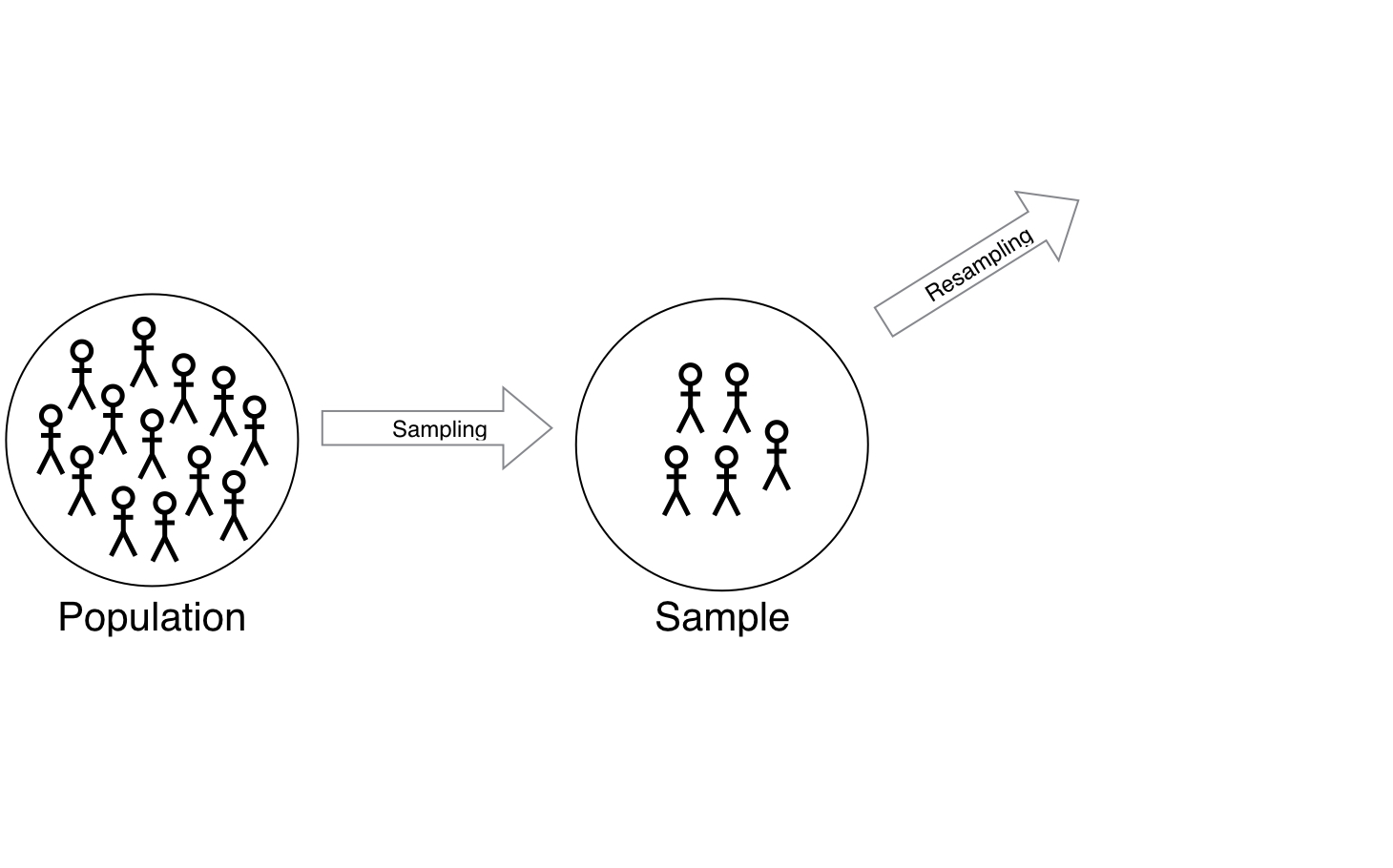
ch4_2_v4.015.png

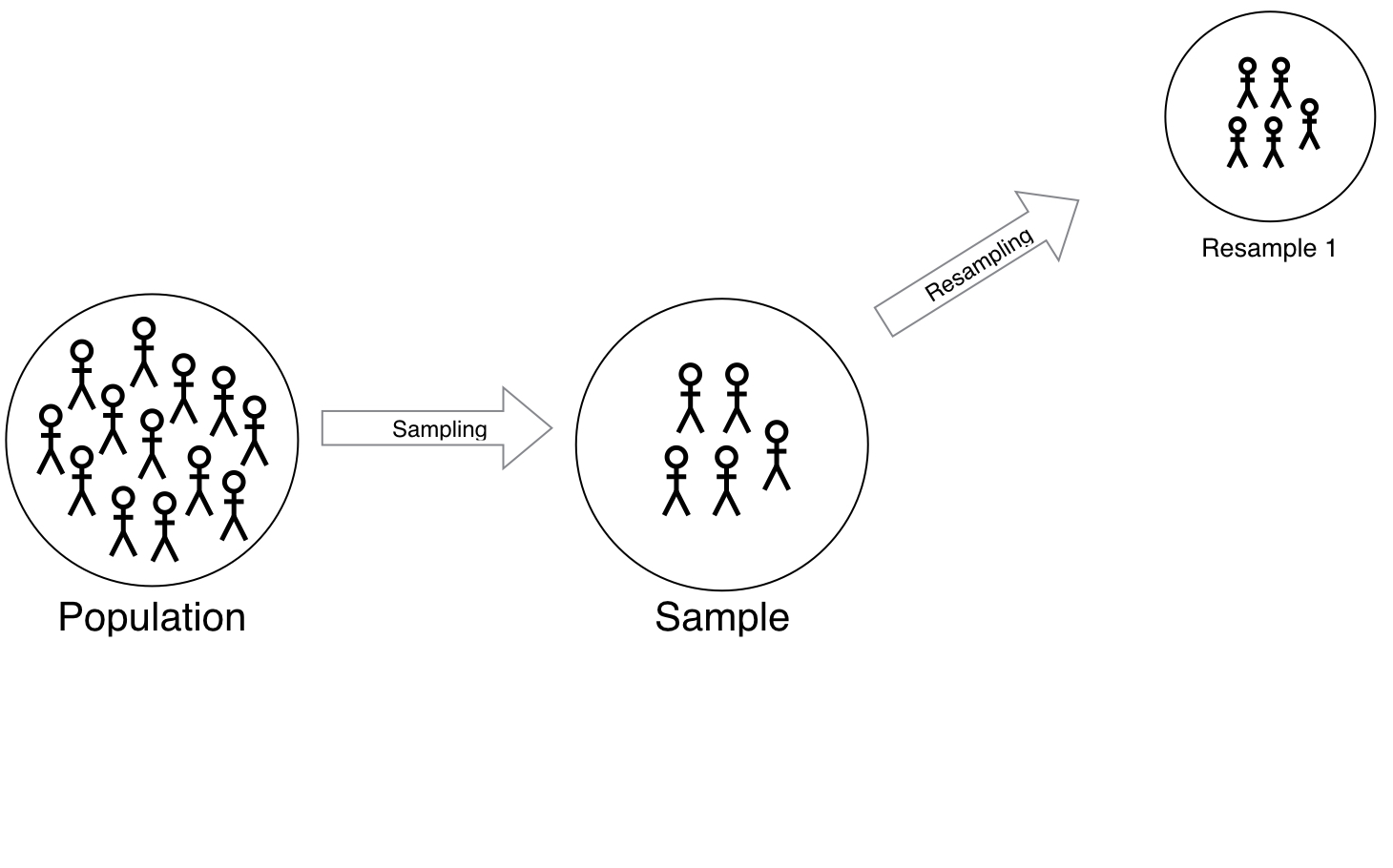
ch4_2_v4.016.png

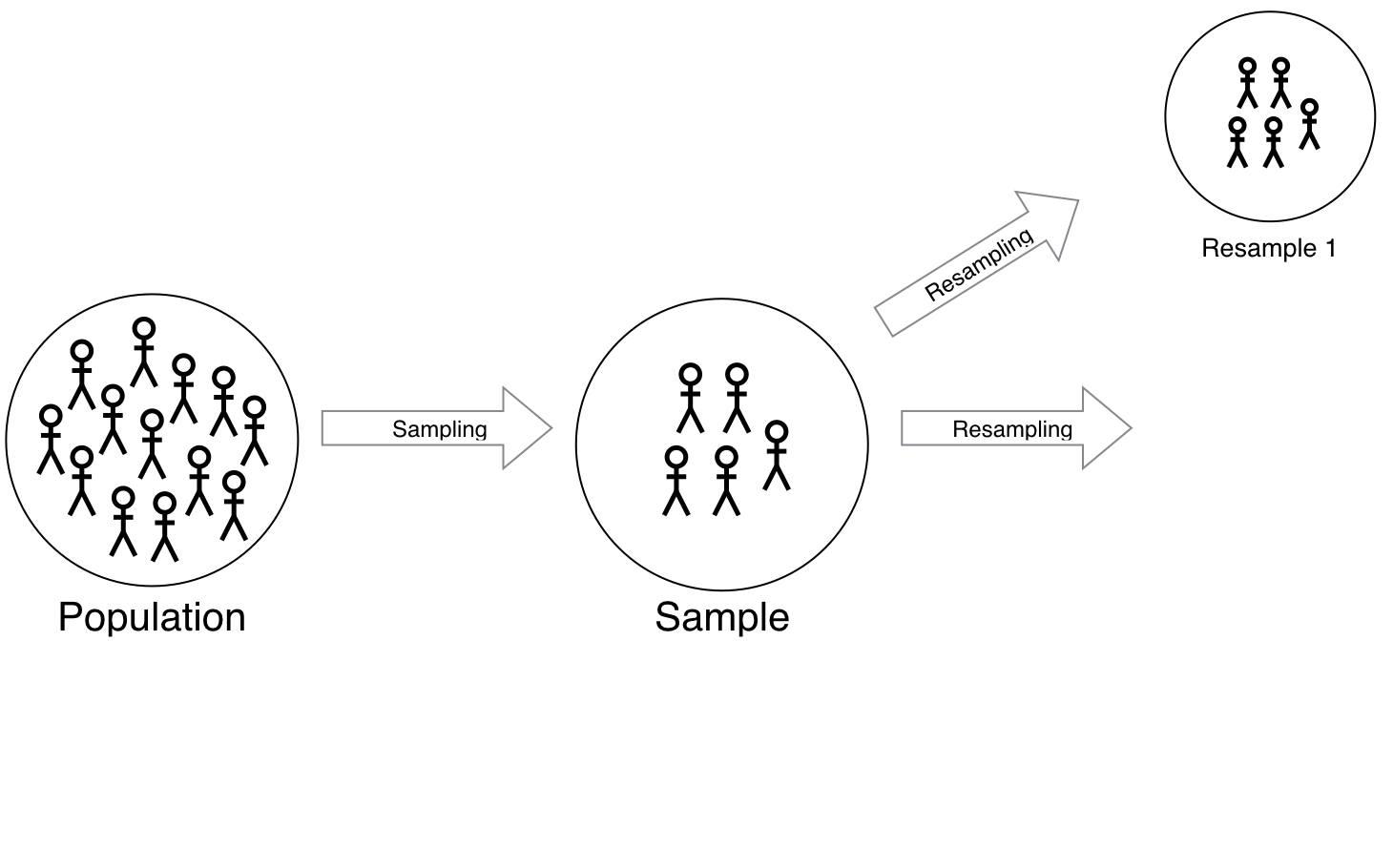
ch4_2_v4.017.png

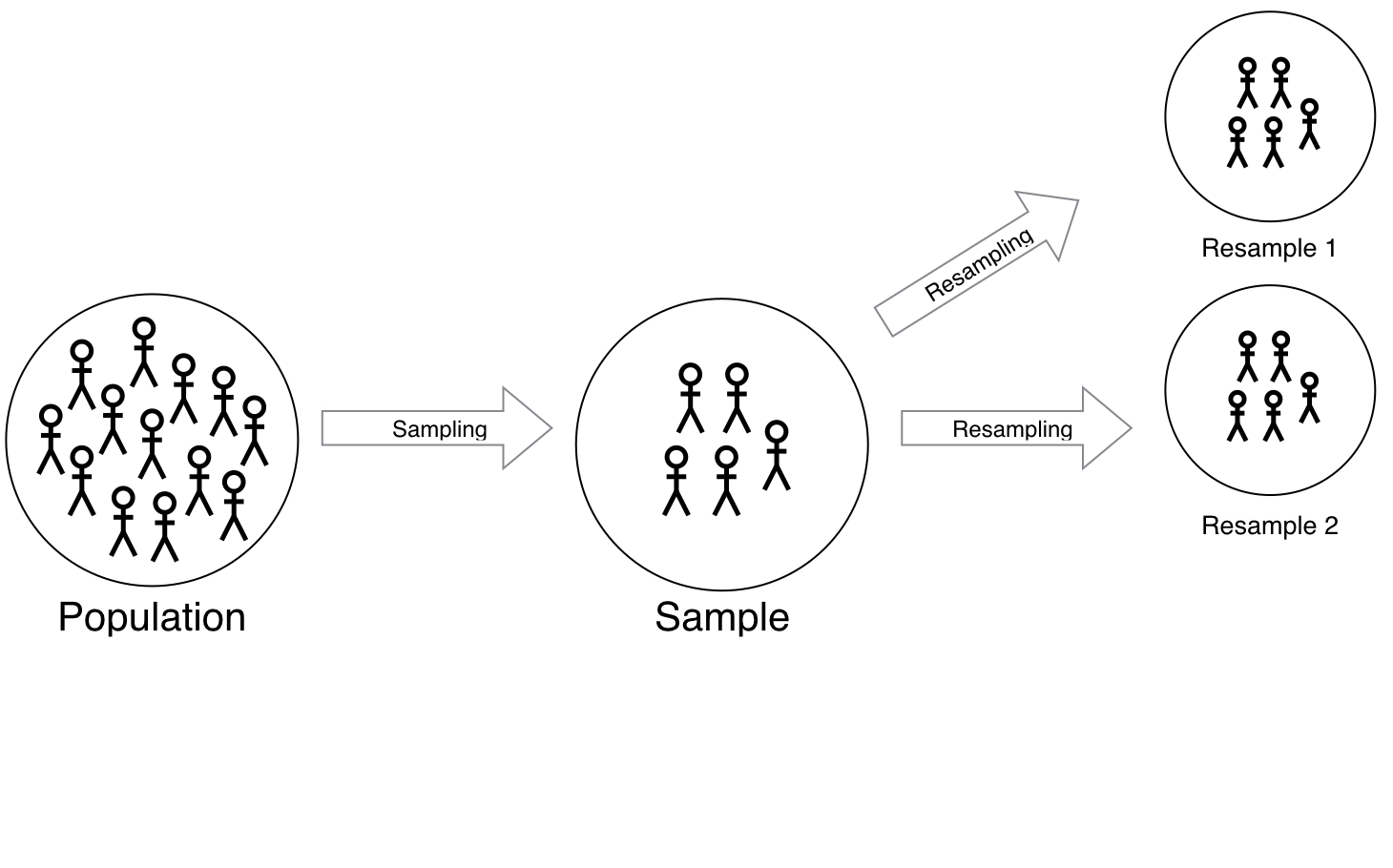
ch4_2_v4.018.png

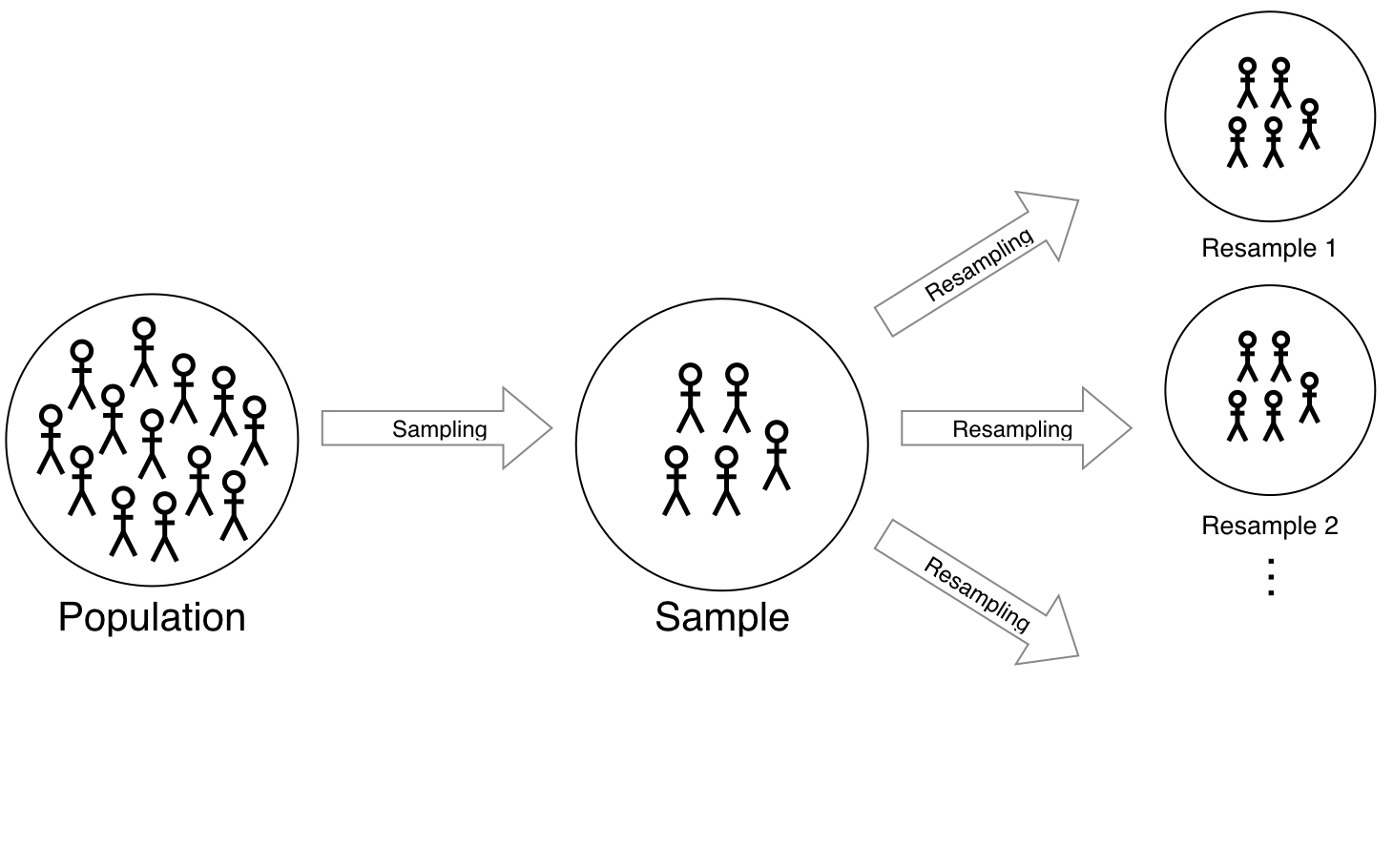
ch4_2_v4.019.png

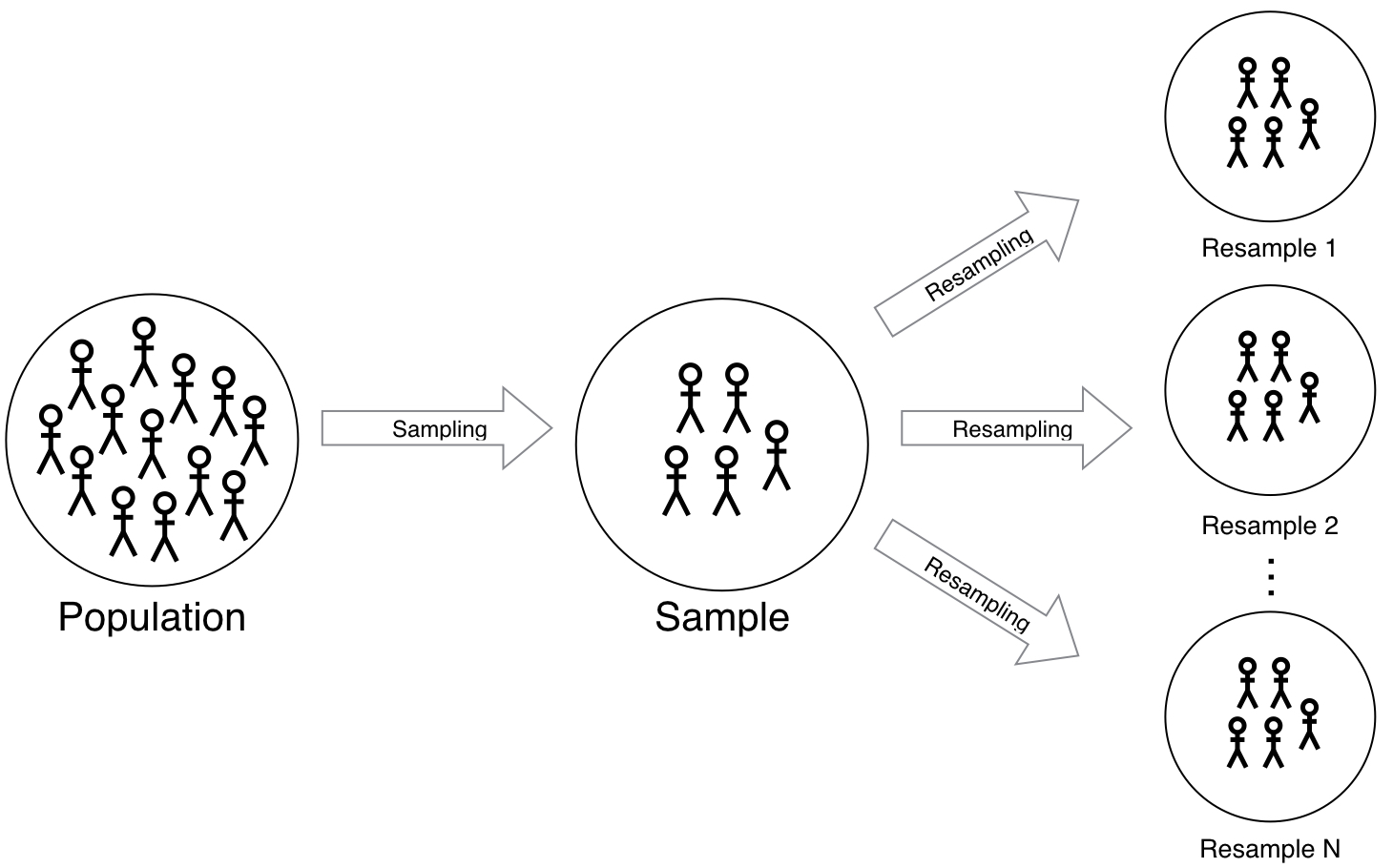
ch4_2_v4.020.png

Polling

# Original data
Source: local data frame [30 x 3]

     flip_num  flip
        <int>  <chr>
1          1       H
2          2       H
3          3       H
4          4       T
5          5       H                
6          6       H
# ... with 24 more rows

Original data

Candidate X	Total voters	Proportion X
17	30	0.5667

Polling

# First resample
Source: local data frame [30 x 3]

   replicate flip_num  flip
       <dbl>    <int> <chr>
1          1        7     H
2          1       17     T
3          1       13     H
4          1       14     H
5          1       24     H
6          1       28     T
# ... with 24 more rows

First resample

Candidate X	Total voters	Proportion X
17	30	0.5667
14	30	0.4667

Polling

# Second resample
Source: local data frame [30 x 3]

   replicate flip_num  flip
       <dbl>    <int> <chr>
1          2       21     H
2          2       19     T
3          2       25     H
4          2       24     T
5          2       21     H
6          2       28     T
7          2       13     H
8          2       23     H
9          2       24     T
10         2       24     T
# ... with 20 more rows

Second resample

Candidate X	Total voters	Proportion X
17	30	0.5667
14	30	0.4667
18	30	0.6

Polling

# Third resample
Source: local data frame [30 x 3]

   replicate flip_num  flip
       <dbl>    <int> <chr>
1          3        6     H
2          3       19     H
3          3        1     H
4          3       24     T
5          3       11     H
6          3       28     T
7          3       16     H
8          3       13     H
9          3       21     T
10         3       29     H
# ... with 20 more rows

Third resample

Candidate X	Total voters	Proportion X
17	30	0.5667
14	30	0.4667
18	30	0.6
12	30	0.4

Standard error

Obtained standard error of 0.09 by resampling many times
Describes how the statistic varies around parameter
Bootstrap provides an approximation of the standard error

Variability of p-hat from the population

# Compute p-hat for each poll
ex1_props <- recommend %>% 
    group_by(poll) %>% 
    summarize(prop_yes = 
                mean(vote == "yes"))

# Variability of p-hat
ex1_props %>% 
    summarize(sd(prop_yes))

# A tibble: 1 × 1
  `sd(prop_yes)`
           <dbl>
1     0.08523512

Variability of p-hat from the sample (bootstrapping)

# Select one poll from which to resample
one_poll <- all_polls %>%
    filter(poll ==1) %>%
    select(vote)

# Compute p-hat for each resampled poll
ex2_props <- one_poll %>%
    specify(response = vote,
            success = "yes") %>%
    generate(reps = 1000,
            type = "bootstrap")

# Variability of p-hat
ex2_props %>% 
    summarize(sd(stat))

# A tibble: 1 × 1
  `sd(stat)`
           <dbl>
1     0.08691885

Let's practice!

Foundations of Inference in R