Mixed seasonal models
ARIMA Models in R

David Stoffer
Professor of Statistics at the University of Pittsburgh
Mixed Seasonal Model
Mixed model: SARIMA$(p, d, q) \times (P, D, Q)_s$ model
Consider a SARIMA$(0, 0, 1) \times (1, 0, 0)_{12}$ model
$$X_t = \Phi X_{t-12} + W_t + \theta W_{t-1}$$
SAR(1): Value this month is related to last year's value $X_{t-12}$
MA(1): This month's value related to last month's shock $W_{t-1}$
ACF and PACF of SARIMA(0,0,1) x (1,0,0) s=12
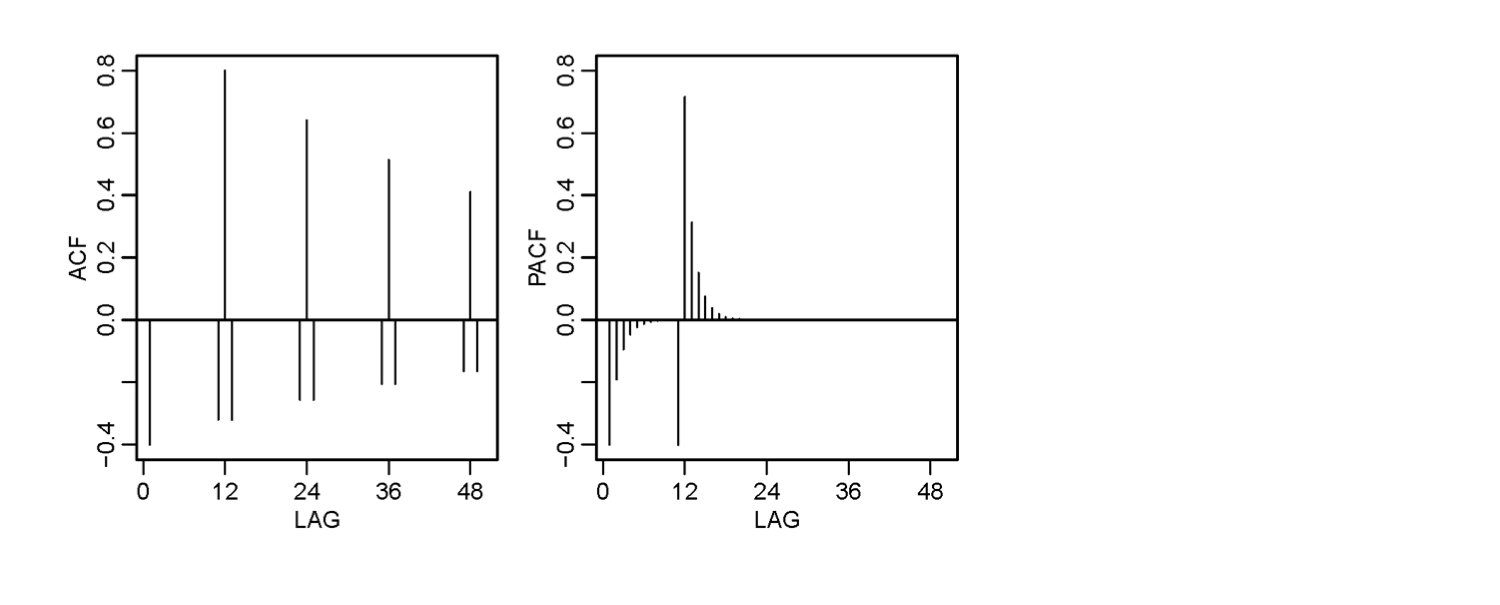
- The ACF and PACF for this mixed model:
$$X_t = .8 X_{t-12} + W_t -.5 W_{t-1}$$
ACF and PACF of SARIMA(0,0,1) x (1,0,0) s=12
- The ACF and PACF for this mixed model:
$$X_t = .8 X_{t-12} + W_t -.5 W_{t-1}$$
ACF and PACF of SARIMA(0,0,1) x (1,0,0) s=12
- The ACF and PACF for this mixed model:
$$X_t = .8 X_{t-12} + W_t -.5 W_{t-1}$$
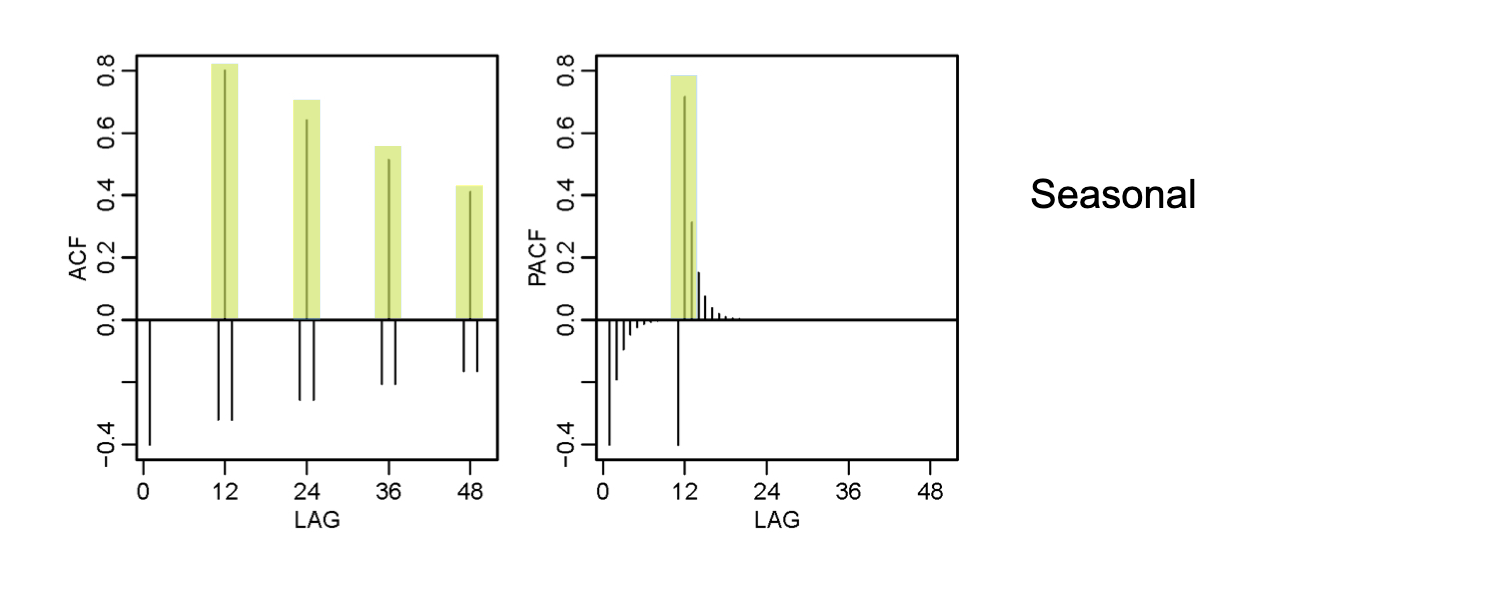
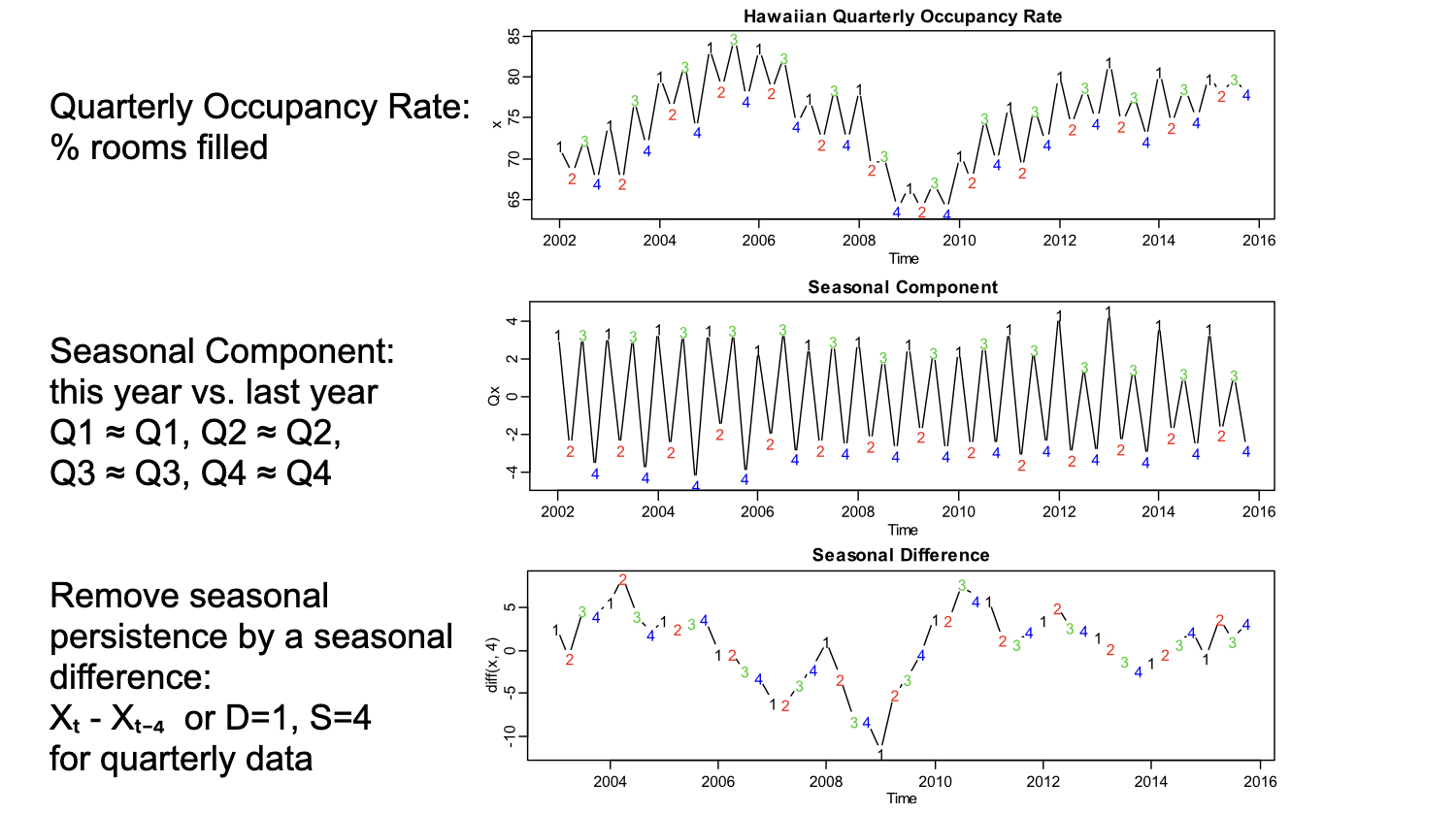
Seasonal Persistence
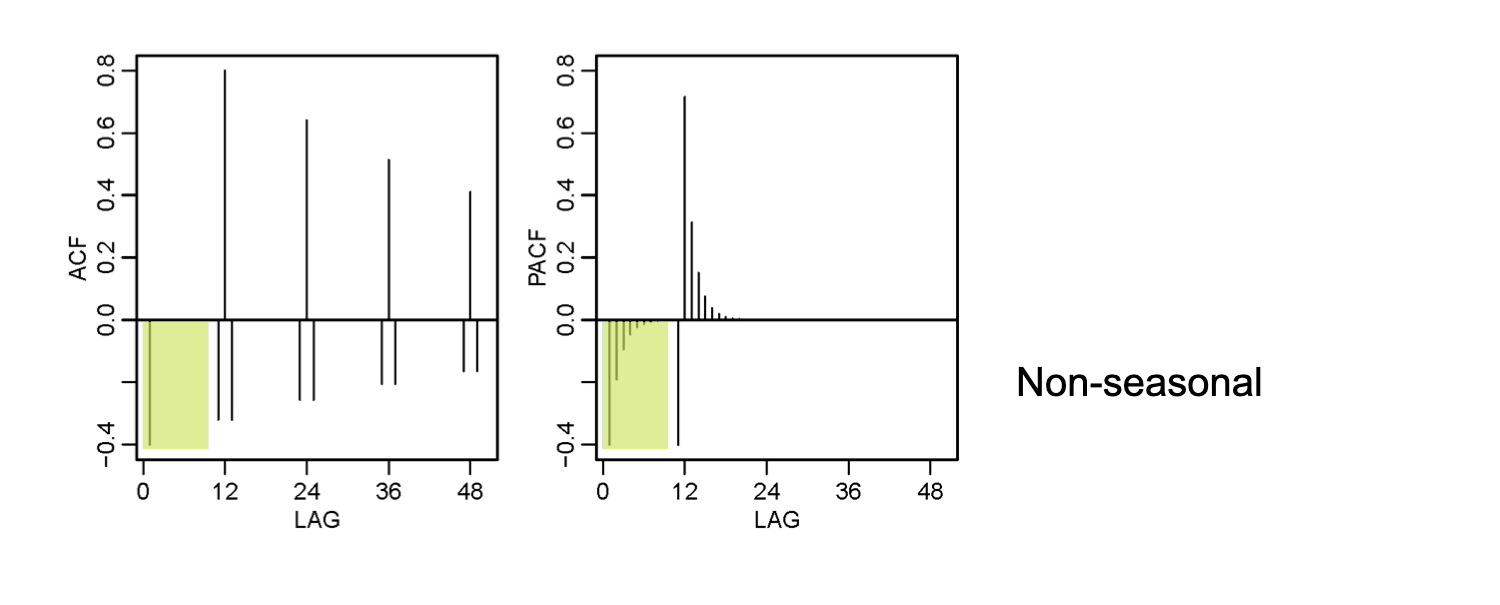
Seasonal Persistence
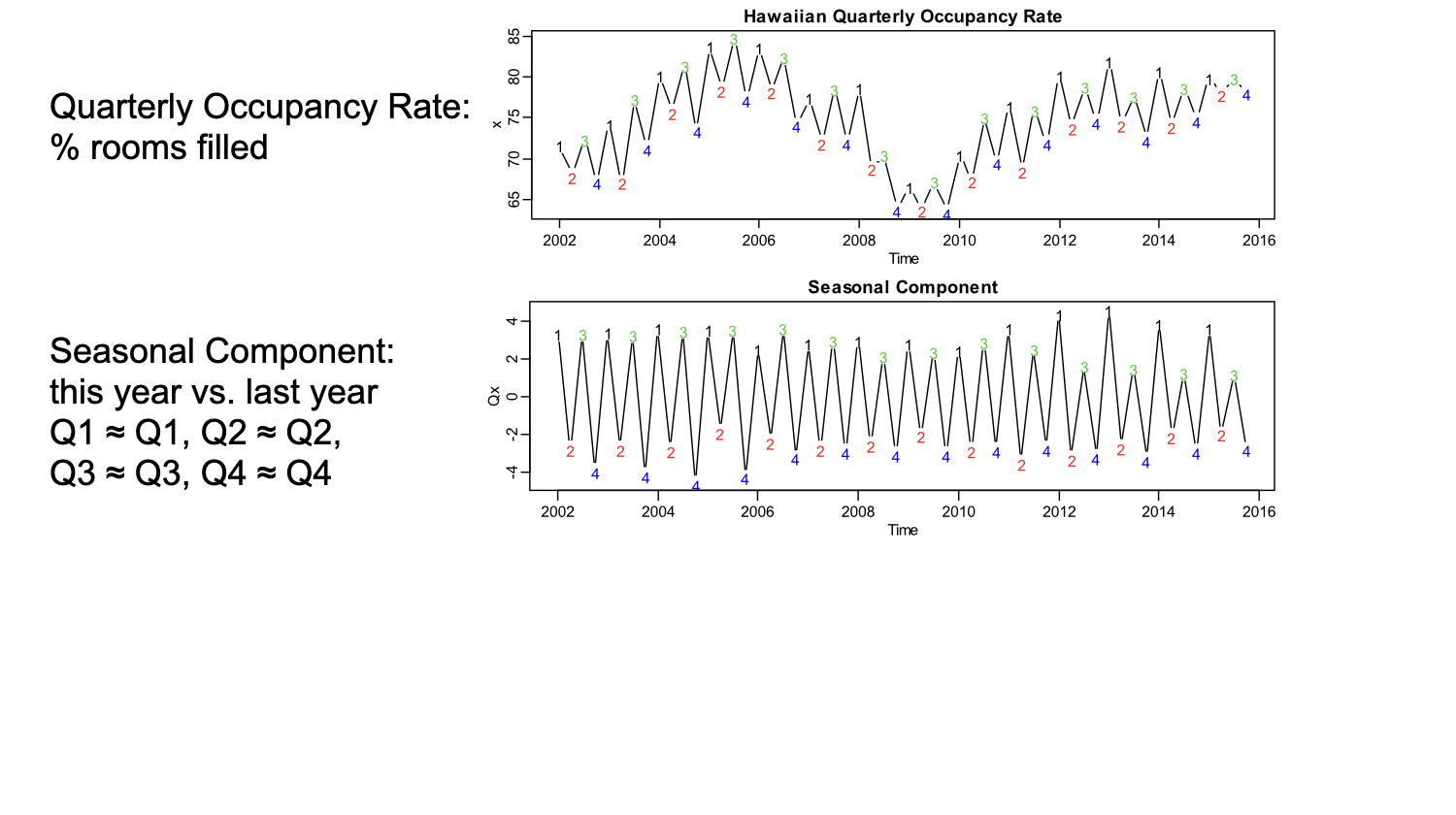
Seasonal Persistence
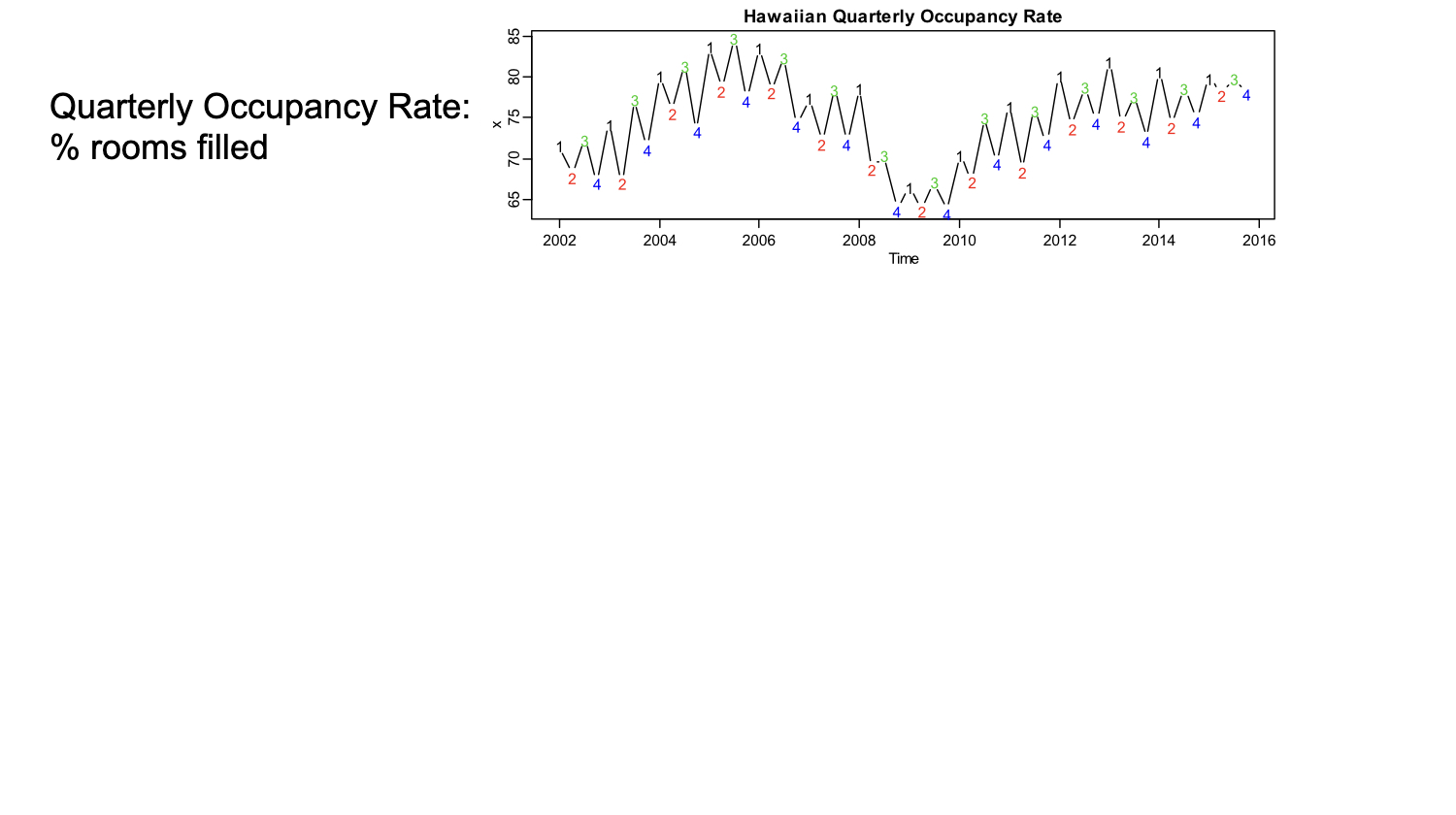
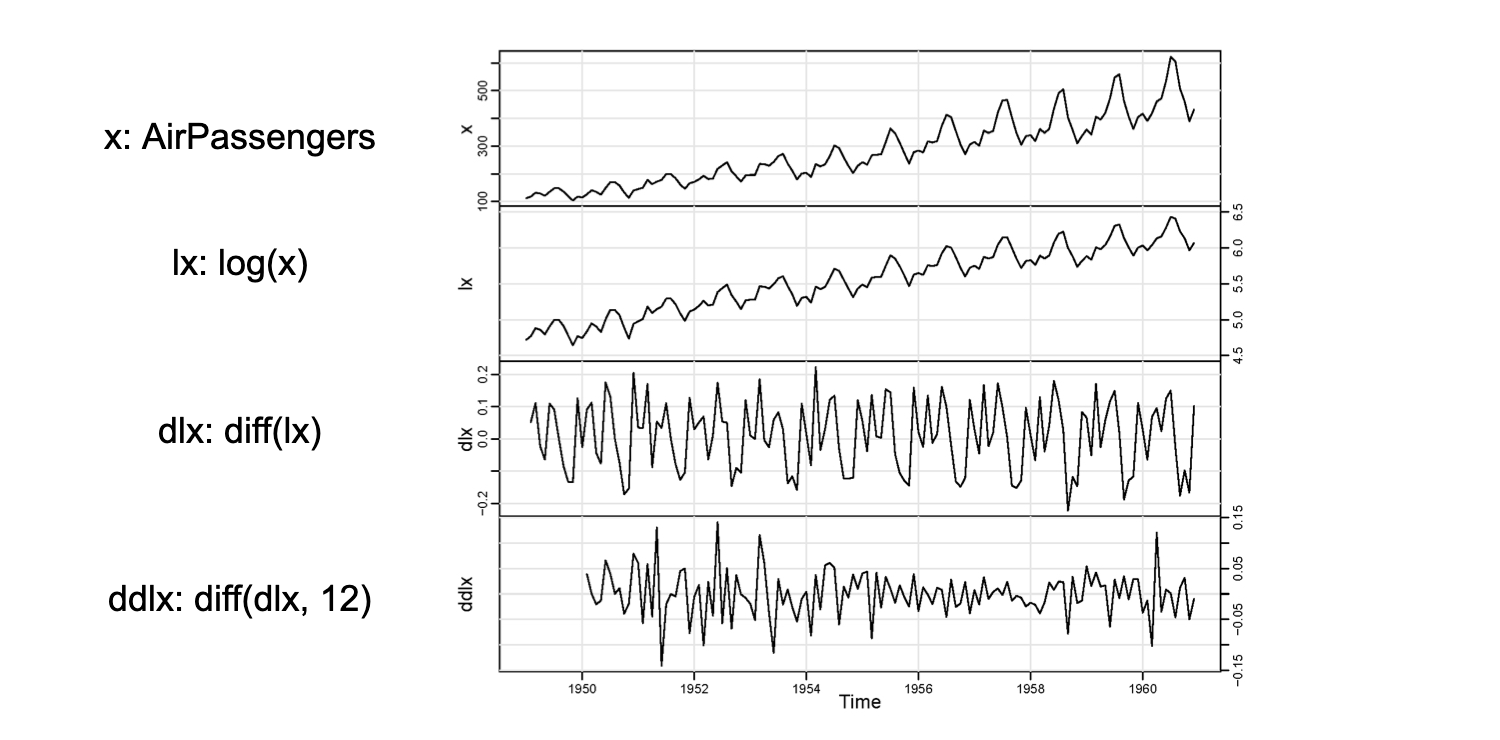
Air Passengers
- Monthly totals of international airline passengers, 1949-1960
Air Passengers: ACF and PACF of ddlx
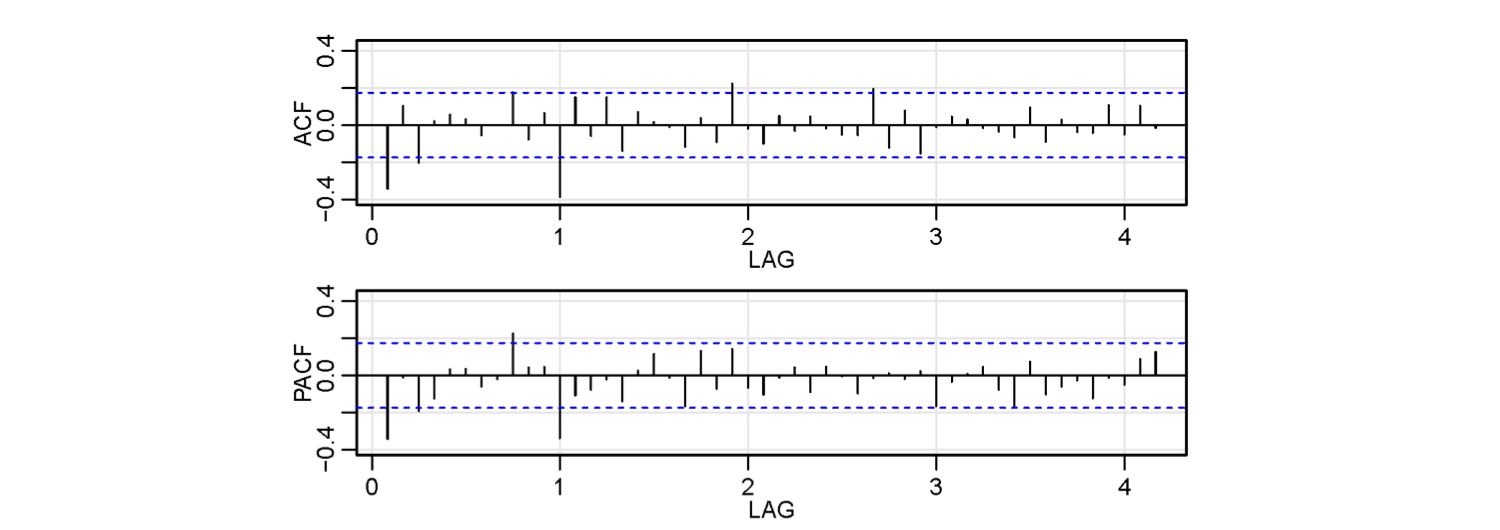
Air Passengers: ACF and PACF of ddlx
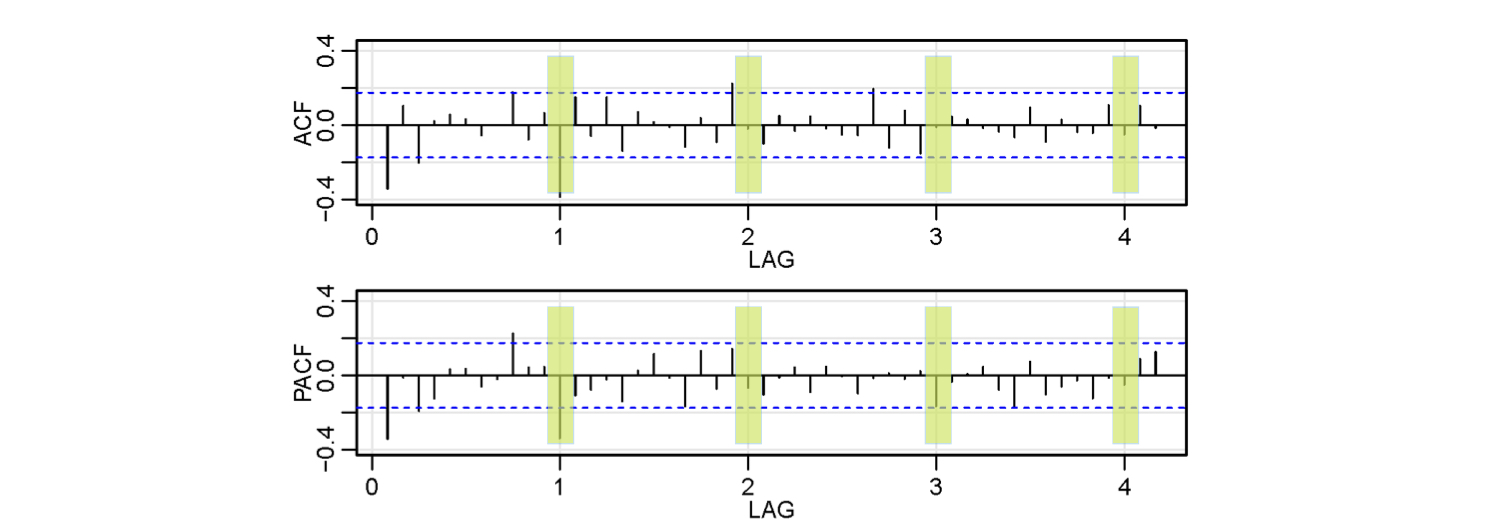
- Seasonal: ACF cutting off at lag 1s (s = 12); PACF tailing off at lags 1s, 2s, 3s…
Air Passengers: ACF and PACF of ddlx
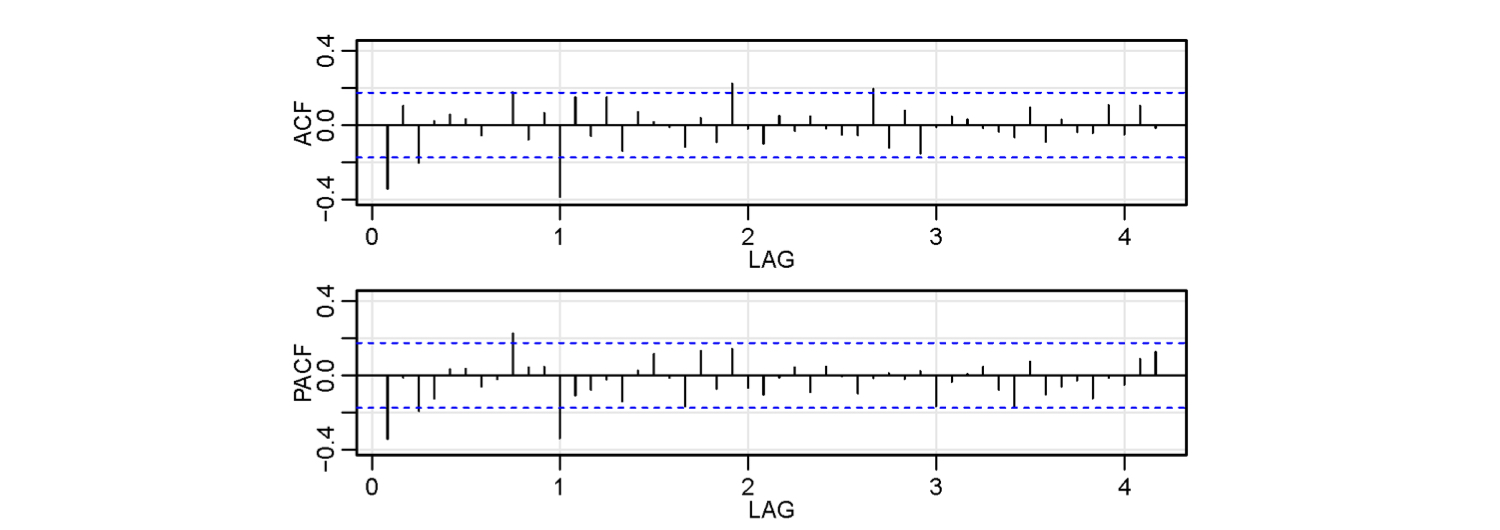
- Seasonal: ACF cutting off at lag 1s (s = 12); PACF tailing off at lags 1s, 2s, 3s…
Air Passengers: ACF and PACF of ddlx
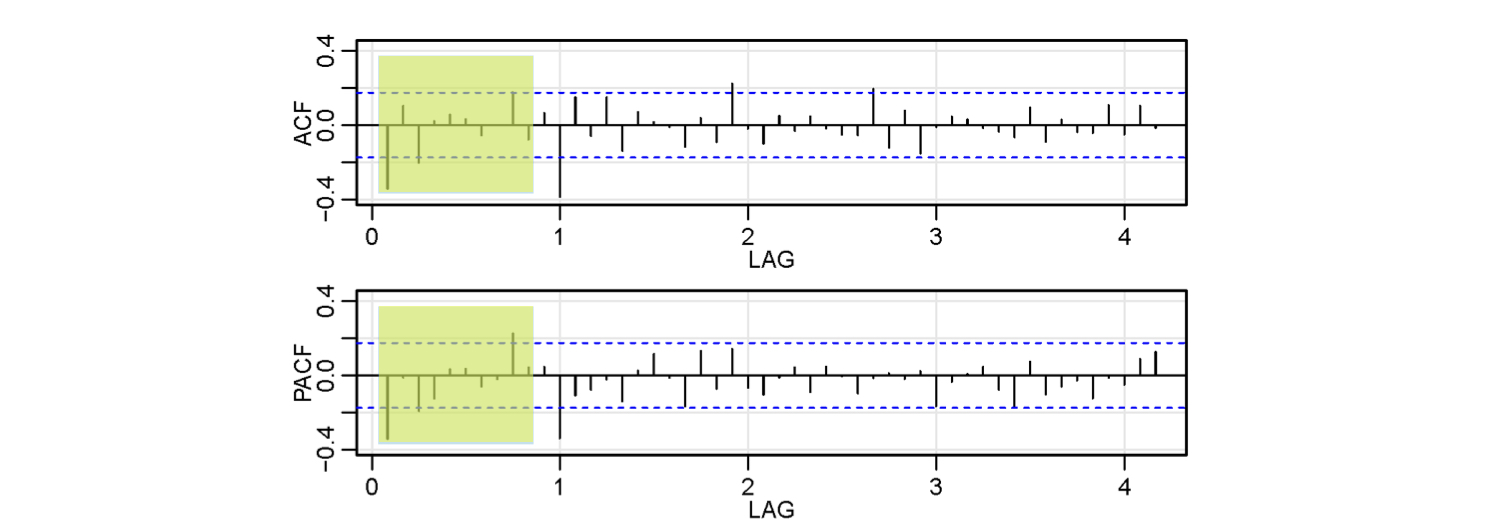
Seasonal: ACF cutting off at lag 1s (s = 12); PACF tailing off at lags 1s, 2s, 3s…
Non-Seasonal: ACF and PACF both tailing off
Air Passengers
airpass_fit1 <- sarima(log(AirPassengers), p = 1,
d = 1, q = 1, P = 0,
D = 1, Q = 1, S = 12)
airpass_fit1$ttable
Estimate SE t.value p.value
ar1 0.1960 0.2475 0.7921 0.4296
ma1 -0.5784 0.2132 -2.7127 0.0075
sma1 -0.5643 0.0747 -7.5544 0.0000
airpass_fit2 <- sarima(log(AirPassengers), 0, 1, 1, 0, 1, 1, 12)
airpass_fit2$ttable
Estimate SE t.value p.value
ma1 -0.4018 0.0896 -4.4825 0
sma1 -0.5569 0.0731 -7.6190 0
Air Passengers
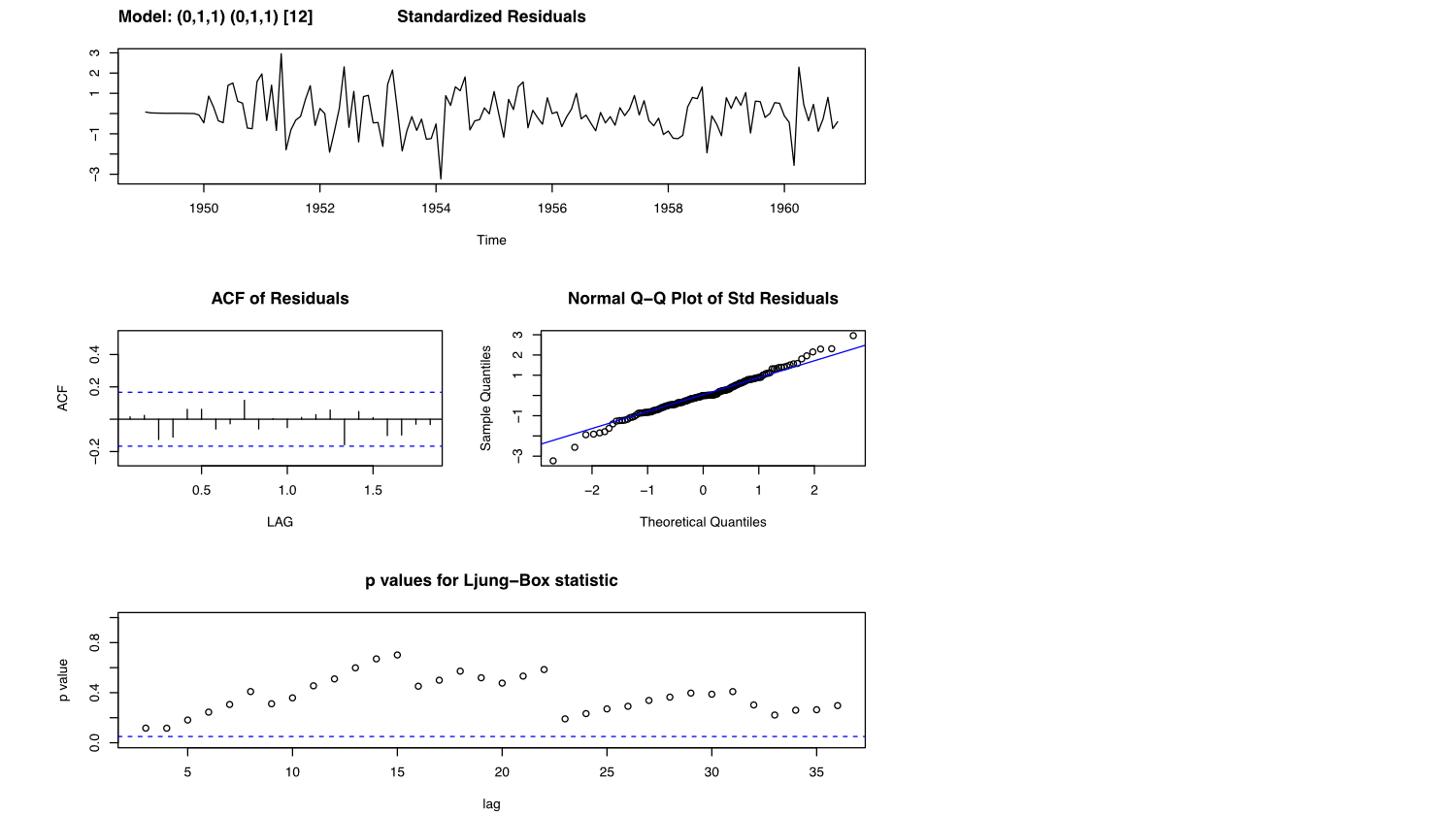
Let's practice!
ARIMA Models in R

