Measuring risk of a portfolio

Introduction to Portfolio Analysis in Python

Charlotte Werger

Data Scientist

Risk of a portfolio

Investing is risky: individual assets will go up or down
Expected return is a random variable
Returns spread around the mean is measured by the variance $\sigma^2$ and is a common measure of volatility
$\sigma^2 = \frac{\sum\limits_{i=1}^N (X -\mu)^2}{N}$

Risk as a balancing act

Variance

Variance of an individual asset varies: some have more or less spread around the mean
Variance of the portfolio is not simply the weighted variances of the underlying assets
Because returns of assets are correlated, it becomes complex

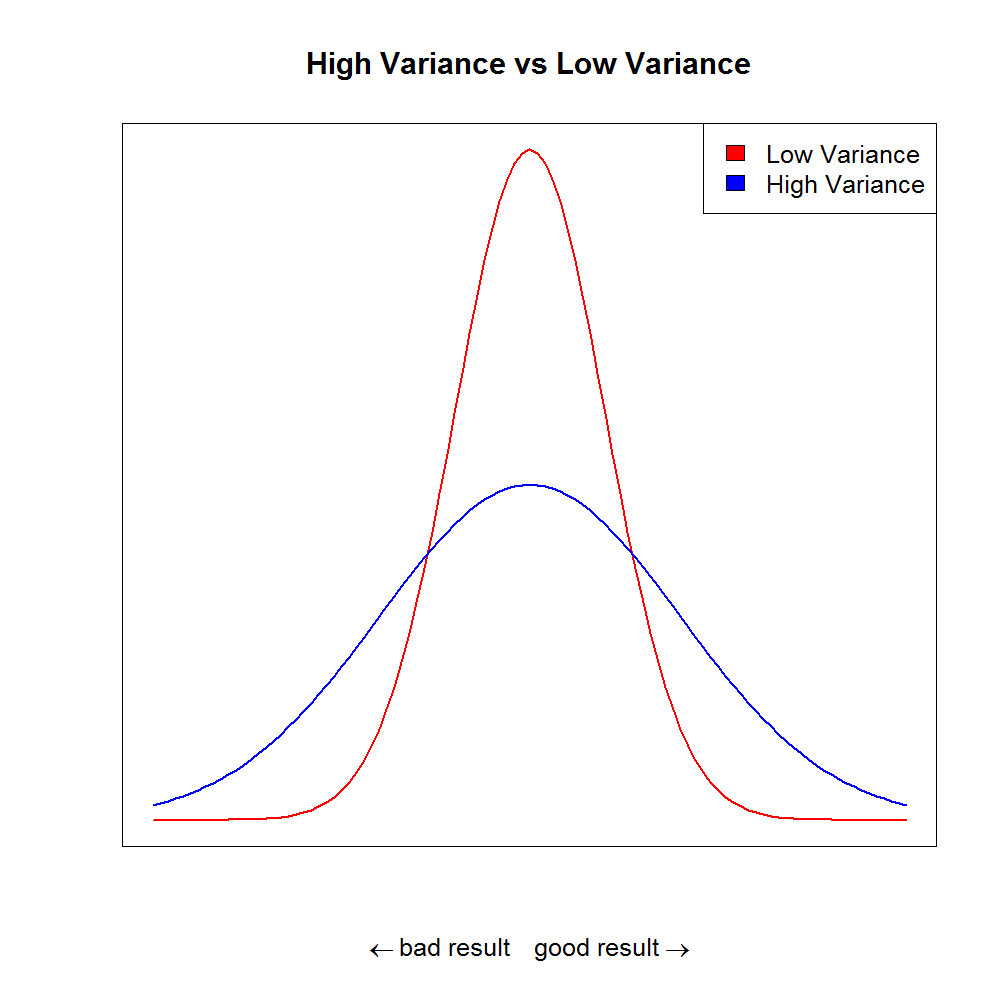
Distributions with high and low variance

How do variance and correlation relate to portfolio risk?

The correlation between asset 1 and 2 is denoted by $\rho_{1,2}$, and tells us to which extend assets move together
The portfolio variance takes into account the individual assets' variances ($\sigma_1^2, \sigma_2^2, etc$), the weights of the assets in the portfolio ($w_1, w_2$), as well as their correlation to each other
The standard deviation ($\sigma$) is equal to the square root of variance ($\sigma^2$), both are a measure of volatility

Calculating portfolio variance

$$ Formula for portfolio variance

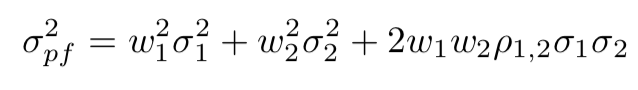
$\rho_{1,2} \sigma_1 \sigma_2$ is called the covariance between asset 1 and 2
The covariance can also be written as $ \sigma_{1,2} $
This let's us write:

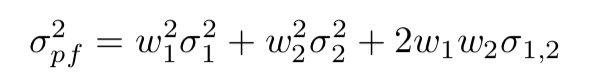
Formula for portfolio variance re-written

Re-writing the portfolio variance shorter

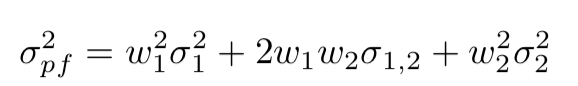
Formula for portfolio variance

This can be re-written in matrix notation, which you can use more easily in code:

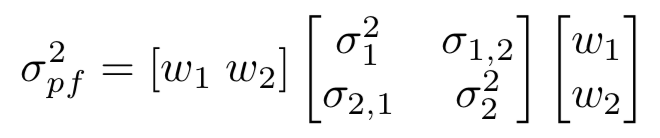
Portfolio variance in matrix notation

In words, what we need to calculate in python is:

Portfolio variance = Weights transposed x (Covariance matrix x Weights)

Portfolio variance in python

price_data.head(2)

ticker        AAPL       FB        GE       GM       WMT
date                    
2018-03-21    171.270    169.39    13.88    37.58    88.18
2018-03-22    168.845    164.89    13.35    36.35    87.14

# Calculate daily returns from prices
daily_returns = df.pct_change()

# Construct a covariance matrix for the daily returns data
cov_matrix_d = daily_returns.cov()

Portfolio variance in python

# Construct a covariance matrix from the daily_returns
cov_matrix_d = (daily_returns.cov())*250
print (cov_matrix_d)

        AAPL          FB          GE          GM          WMT                    
AAPL    0.053569    0.026822    0.013466    0.018119    0.010798
FB      0.026822    0.062351    0.015298    0.017250    0.008765
GE      0.013466    0.015298    0.045987    0.021315    0.009513
GM      0.018119    0.017250    0.021315    0.058651    0.011894
WMT     0.010798    0.008765    0.009513    0.011894    0.041520

weights = np.array([0.2, 0.2, 0.2, 0.2, 0.2])

Portfolio variance in python

# Calculate the variance with the formula
port_variance = np.dot(weights.T, np.dot(cov_matrix_a, weights))
print (port_variance)

0.022742232726360567

# Just converting the variance float into a percentage
print(str(np.round(port_variance, 3) * 100) + '%')

2.3%

port_stddev = np.sqrt(np.dot(weights.T, np.dot(cov_matrix_a, weights)))
print(str(np.round(port_stddev, 3) * 100) + '%')
15.1%

Let's practice!

Introduction to Portfolio Analysis in Python