Alternative portfolio optimization

Introduction to Portfolio Analysis in Python

Charlotte Werger

Data Scientist

Expected risk and return based on historic data

Mean historic returns, or the historic portfolio variance are not perfect estimates of mu and Sigma
Weights from portfolio optimization therefore not guaranteed to work well on future data

$$ If history repeats itself joke

Historic data

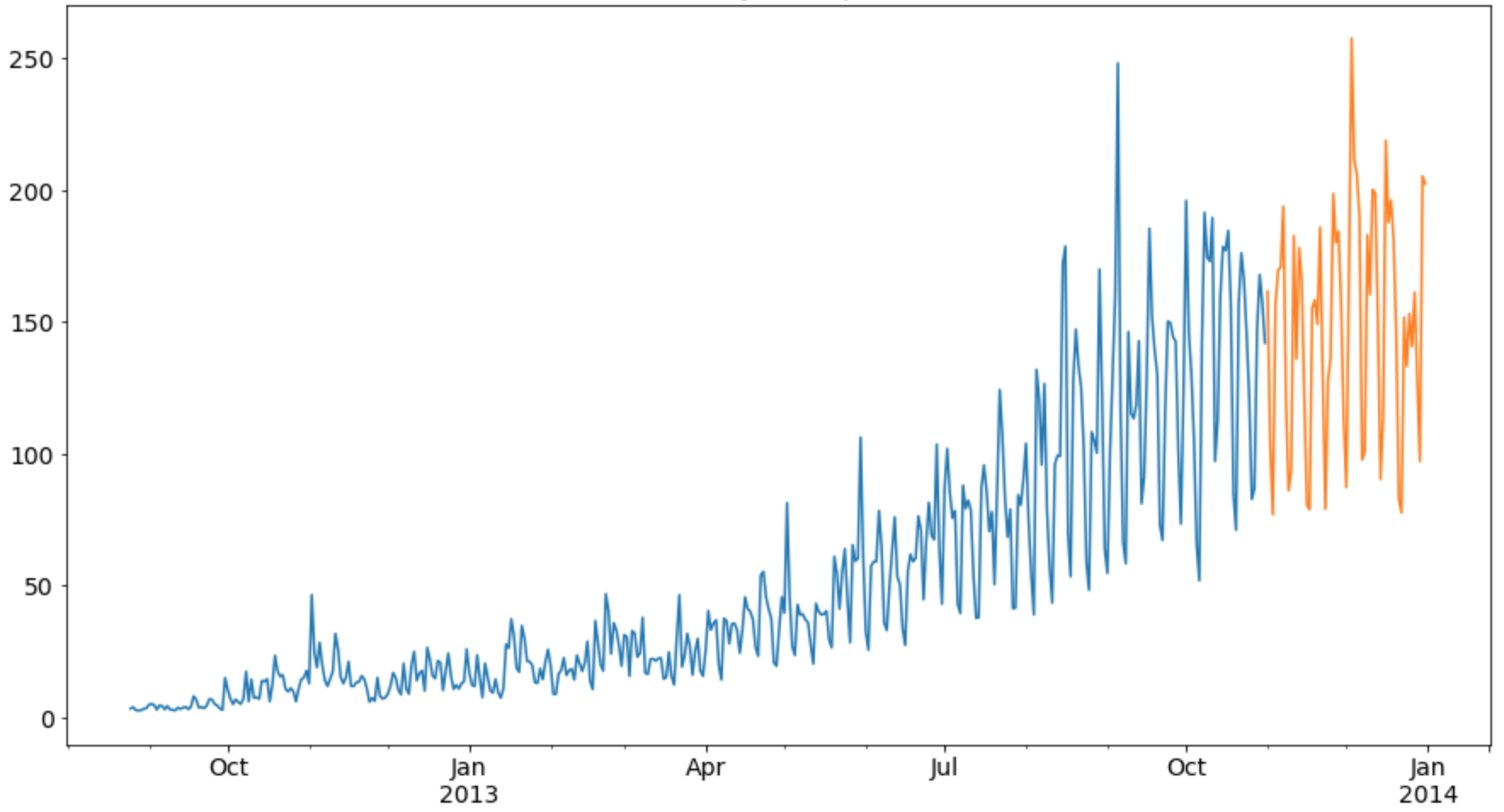
Time series data changing over time

Exponentially weighted returns

Need better measures for risk and return
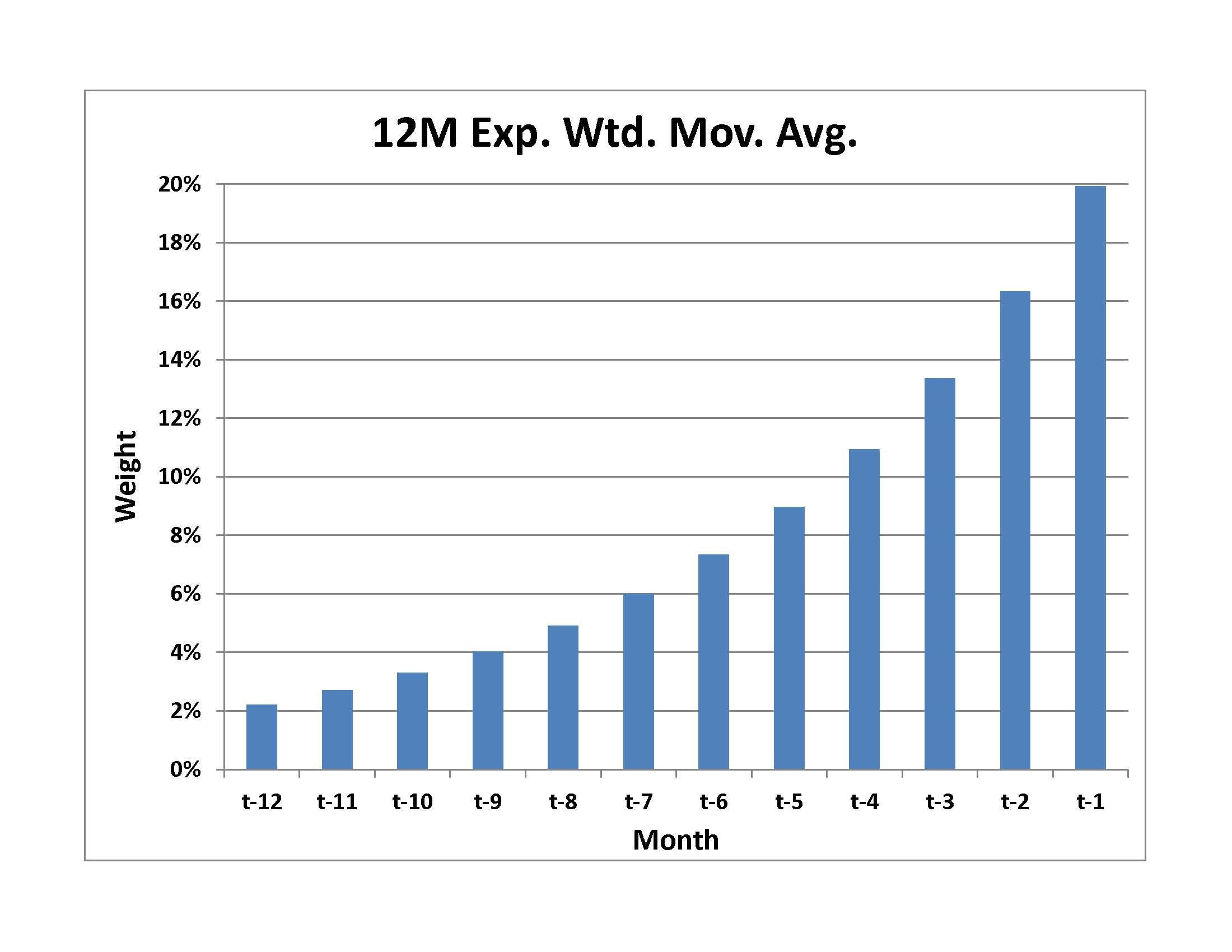
Exponentially weighted risk and return assigns more importance to the most recent data
Exponential moving average in the graph: most weight on t-1 observation

Weights in exponentially weighted returns calculation

Exponentially weighted covariance

The exponential covariance matrix: gives more weight to recent data
In the graph: exponential weighted volatility in black, follows real volatility better than standard volatility in blue

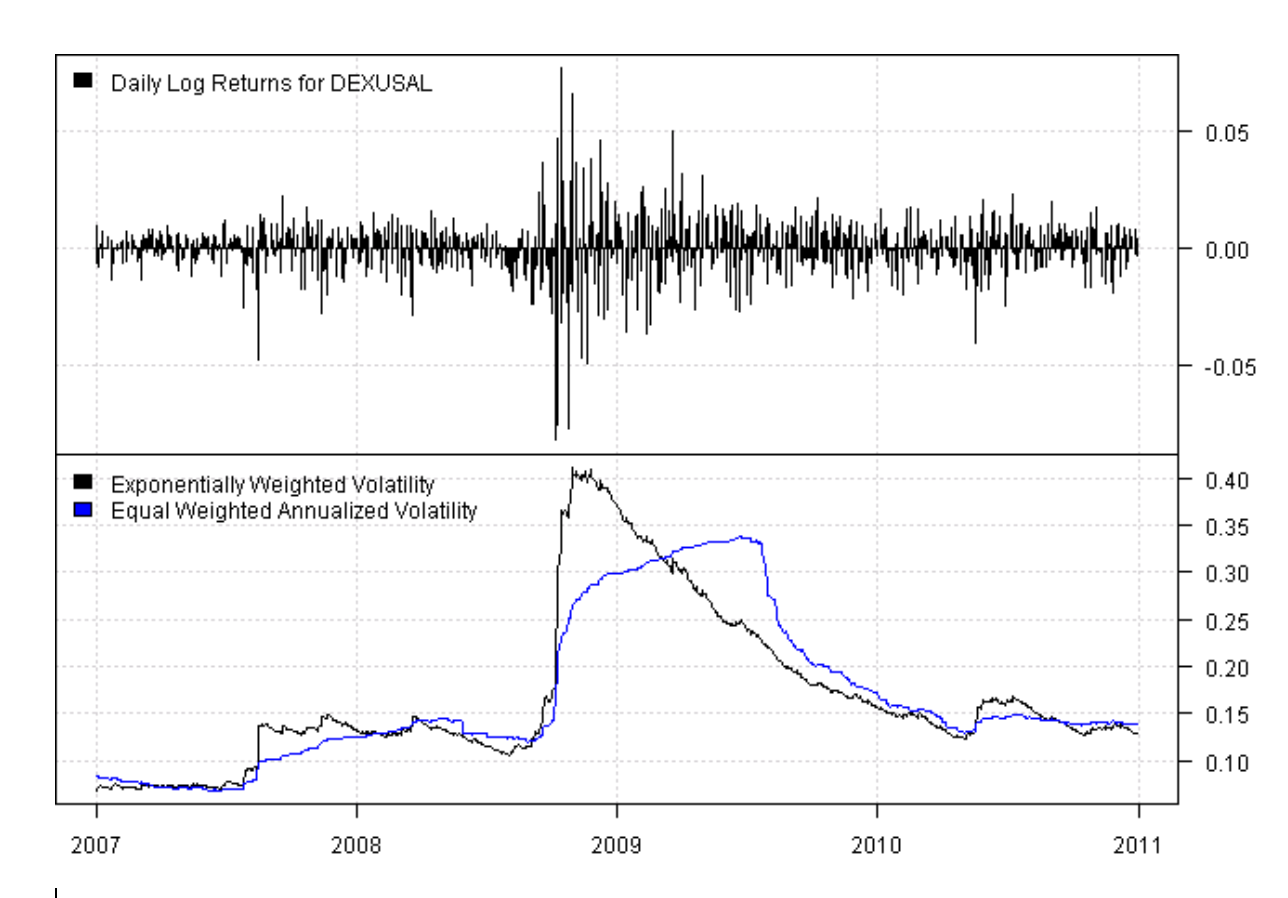
$$ Comparing exponentially weighted covariance and normal covariance to actual covariance

¹ Source: https://systematicinvestor.github.io/Exponentially-Weighted-Volatility-RCPP

Exponentially weighted returns

from pypfopt import expected_returns

# Exponentially weighted moving average
mu_ema = expected_returns.ema_historical_return(df, 
                         span=252, frequency=252)
print(mu_ema)

symbol
XOM     0.103030
BBY     0.394629
PFE     0.186058

Exponentially weighted covariance

from pypfopt import risk_models

# Exponentially weighted covariance
Sigma_ew = risk_models.exp_cov(df, span=180, frequency=252)

Using downside risk in the optimization

$ $

Remember the Sortino ratio: it uses the variance of negative returns only
PyPortfolioOpt allows you to use semicovariance in the optimization, this is a measure for downside risk:

$ $ Calculation of downside risk

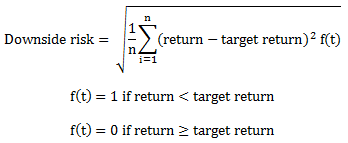
Semicovariance in PyPortfolioOpt

Sigma_semi = risk_models.semicovariance(df,     
                        benchmark=0, frequency=252)

print(Sigma_semi)

         XOM         BBY          MA         PFE
XOM     0.018939    0.008505    0.006568    0.004058
BBY     0.008505    0.016797    0.009133    0.004404
MA      0.006568    0.009133    0.018711    0.005373
PFE     0.004058    0.004404    0.005373    0.008349

Let's practice!

Introduction to Portfolio Analysis in Python