Item combinations

Market Basket Analysis in R

Christopher Bruffaerts

Statistician

Back to the grocery store

What's in the store?

all_products_emoticons

What are you up for today?

bread_3cheese

{"Bread", "Cheese", "Cheese", "Cheese"}

Focus of market basket analysis

bread_cheese

{"Bread", "Cheese"}

Subsets and supersets

My store - set

X = {"Bread", "Butter", "Cheese", "Wine"}

all_products_emoticons

Subsets of X - itemsets

Size 0: { ${ \emptyset }$ }
Size 1: {"Bread"}, {"Wine"}, ...
Size 2: {"Bread", "Wine"}, ...

Supersets

{"Bread", "Butter"} superset of {"Bread"}
{"Bread", "Butter", "Cheese", "Wine"} superset of {"Bread", "Butter"}

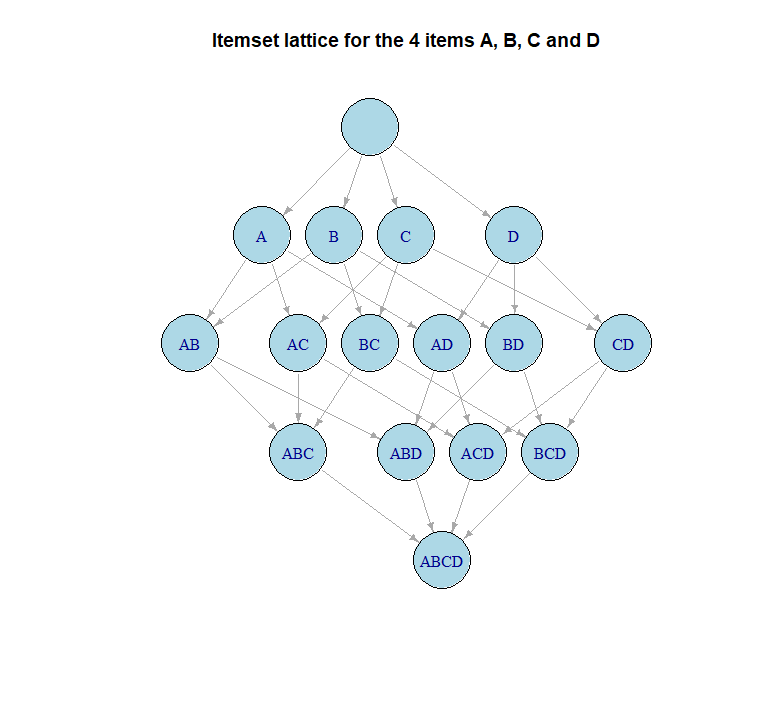
Itemset graph

Question:

What is the set of all possible subsets of X?

X = {A, B, C, D}

itemset_lattice

Intersections and unions

Intersection

{"Bread"} $\cap$ {"Butter"} = $\emptyset$

{"Bread", "Butter"} $\cap$ {"Butter", "Wine"} = {"Butter"}

library(dplyr)
A = c("Bread", "Butter")
B = c("Bread", "Wine")
intersect(A,B)

[1] "Bread"

Union

{"Bread"} $\cup$ {"Butter"} = {"Bread", "Butter"}

union(A,B)

[1] "Bread"  "Butter" "Wine"

How many baskets of size k?

Question:

How many possible subsets of size k from a set of size n ?

"n choose k"

$${n \choose k} = \dfrac{n!}{(n-k)! k!},$$ where

$n! = n \times (n-1) \times (n-2) \times ...\times 2 \times 1$

Example:

Number of baskets with 2 distinct items from the store:

all_products_emoticons

$${4 \choose 2} = \dfrac{4!}{(4-2)! 2!} = 6$$

How many possible baskets?

Question

How many possible baskets can be created from a set of size n ?

Newton's binom

$$\sum_{k=0}^n{n \choose k} = 2^n$$

2^(n_items)

Example

Total number of baskets:

$$2^4 = 16$$

all_products_emoticons

How many baskets in R?

Combinations in R

n_items = 4
basket_size = 2
choose(n_items, basket_size)

[1] 6

# Looping through all possible values
store = matrix(NA, nrow=5, ncol=2)
for (i in 0:n_items){
  store[i+1,] = c(i, choose(n_items,i))}

Output

colnames(store)=c("size", "nb_combi")
store

     size nb_combi
[1,]    0        1
[2,]    1        4
[3,]    2        6
[4,]    3        4
[5,]    4        1

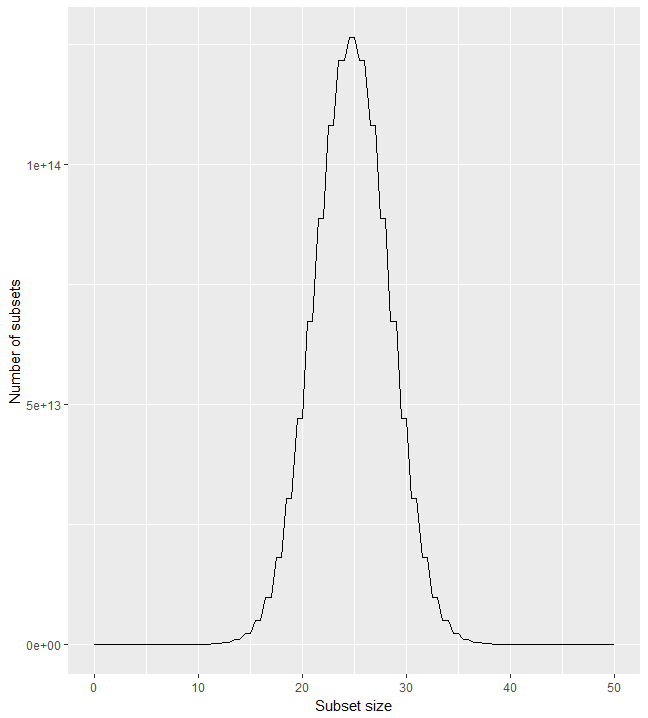
Plotting number of combinations

Get an idea of how fast number of combinations

n_items = 50
fun_nk = function(x) choose(n_items, x)
# Plotting
ggplot(data = data.frame(x = 0),
    mapping = aes(x=x))+
  stat_function(fun = fun_nk)+
  xlim(0, n_items)+
  xlab("Subset size")+
  ylab("Number of subsets")

distribution_combinations

Are you ready to count?

Market Basket Analysis in R