Parametric Estimation
Quantitative Risk Management in Python

Jamsheed Shorish
Computational Economist
A class of distributions
- Loss distribution: not known with certainty
- Class of possible distributions?
- Suppose class of distributions $f(x; \theta)$
- $x$ is loss (random variable)
- $\theta$ is vector of unknown parameters
- Example: Normal distribution
- Parameters: $\theta = (\mu, \sigma)$, mean $\mu$ and standard deviation $\sigma$
- Parametric estimation: find 'best' $\theta^\star$ given data
- Loss distribution: $f(x,\theta^\star)$
Fitting a distribution
- Fit distribution according to error-minimizing criteria
- Example:
scipy.stats.norm.fit(), fitting Normal distribution to data- Result: optimally fitted mean and standard deviation
- Example:
- Advantages:
- Can visualize difference between data and estimate using histogram
- Can provide goodness-of-fit tests
Goodness of fit
- How well does an estimated distribution fit the data?
- Visualize: plot histogram of portfolio losses
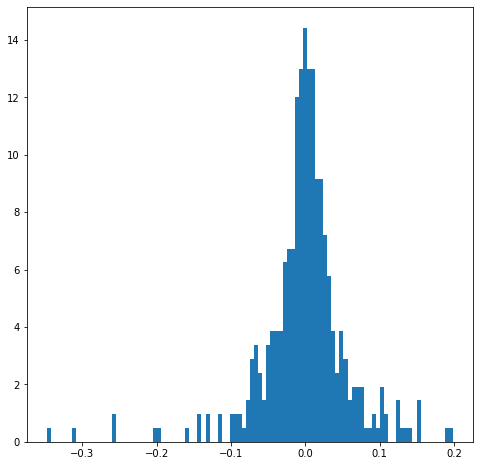
Goodness of fit
- How well does an estimated distribution fit the data?
- Visualize: plot histogram of portfolio losses
- Normal distribution with
norm.fit()
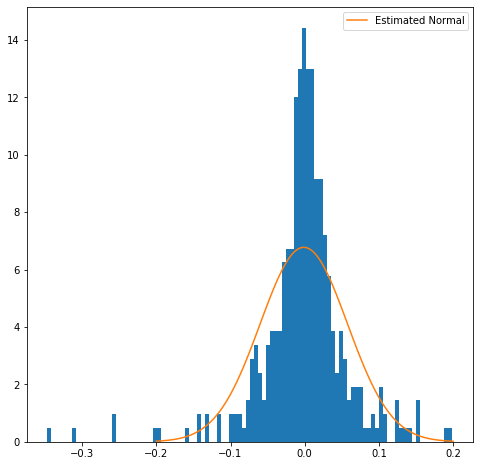
Goodness of fit
- How well does an estimated distribution fit the data?
- Visualize: plot histogram of portfolio losses
- Example:
- Normal distribution with
norm.fit() - Student's t-distribution with
t.fit() - Asymmetrical histogram?
- Normal distribution with
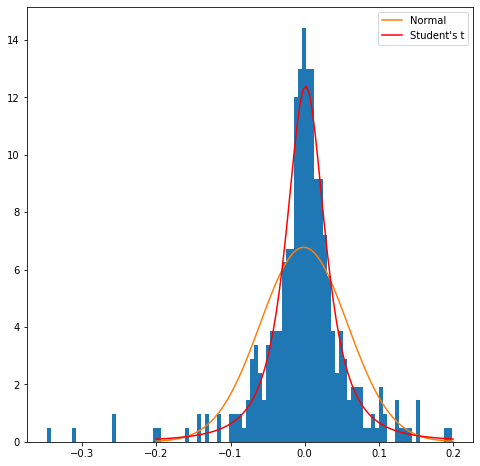
Anderson-Darling test
- Statistical test of goodness of fit
- Test null hypothesis: data are Normally distributed
- Test statistic rejects Normal distribution if larger than
critical_values
- Import
scipy.stats.anderson - Compute test result using
lossdata
from scipy.stats import andersonanderson(loss)
AndersonResult(statistic=11.048641503898523,
critical_values=array([0.57 , 0.649, 0.779, 0.909, 1.081]),
significance_level=array([15. , 10. , 5. , 2.5, 1. ]))
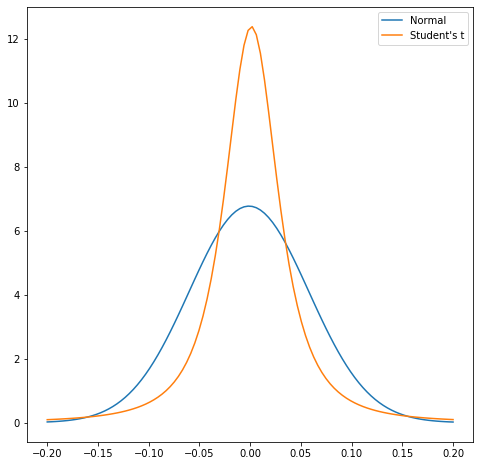
Skewness
- Skewness: degree to which data is non-symmetrically distributed
- Normal distribution: symmetric
Skewness
- Skewness: degree to which data is non-symmetrically distributed
- Normal distribution: symmetric
- Student's t-distribution: symmetric
Skewness
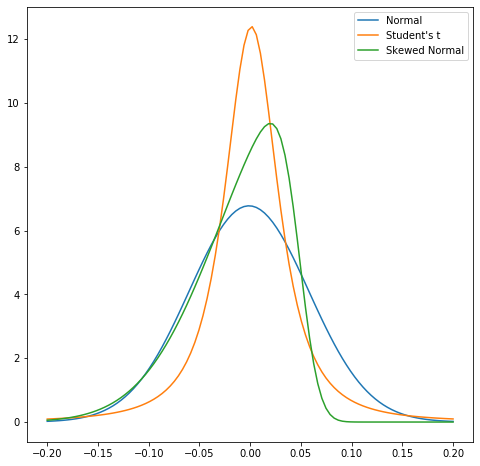
- Skewness: degree to which data is non-symmetrically distributed
- Normal distribution: symmetric
- Student's t-distribution: symmetric
- Skewed Normal distribution: asymmetric
- Contains Normal as special case
- Useful for portfolio data, where e.g. losses more frequent than gains
- Available in
scipy.statsasskewnorm
Testing for skewness
- Test how far data is from symmetric distribution:
scipy.stats.skewtest - Null hypothesis: no skewness
- Import
skewtestfromscipy.stats - Compute test result on
lossdata- Statistically significant => use distribution class with skewness
from scipy.stats import skewtestskewtest(loss)
SkewtestResult(statistic=-7.786120875514511,
pvalue=6.90978472959861e-15)
Let's practice!
Quantitative Risk Management in Python

