Structural breaks
Quantitative Risk Management in Python

Jamsheed Shorish
Computational Economist
Risk and distribution
- Risk management toolkit
- Risk mitigation: MPT
- Risk measurement: VaR, CVaR
- Risk: dispersion, volatility
- Variance (standard deviation) as risk definition
- Connection between risk and distribution of risk factors as random variables
Stationarity
- Assumption: distribution is same over time
- Unchanging distribution = stationary
- Global financial crisis period efficient frontier
- Not stationary
- Estimation techniques require stationarity
- Historical: unknown stationary distribution from past data
- Parametric: assumed stationary distribution class
- Monte Carlo: assumed stationary distribution for random draws
Structural breaks
- Non-stationary => perhaps distribution changes over time
- Assume specific points in time for change
- Break up data into sub-periods
- Within each sub-period, assume stationarity
- Structural break(s): point(s) of change
- Change in 'trend' of average and/or volatility of data
Example: China's population growth
- Examine period 1950 - 2019
- Trend is roughly linear...
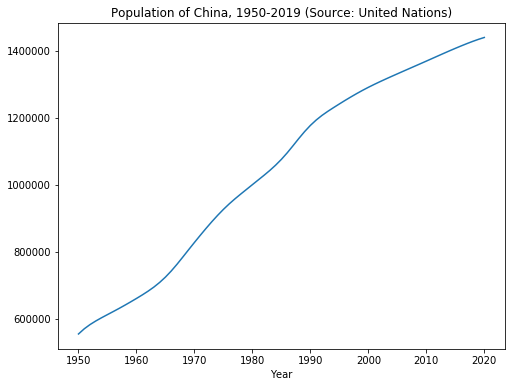
Example: China's population growth
- Examine period 1950 - 2019
- Trend is roughly linear...
- ...but seems to slow down from around 1990
- Possible structural break near 1990.
- Implies distribution of net population (births - deaths) changed
- Possible reasons: government policy, standard of living, etc.
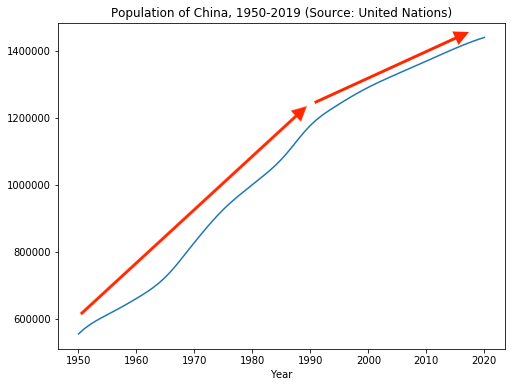
The Chow test
- Previous example: visual evidence for structural break
- Quantification: statistical measure
- Chow Test:
- Test for existence of structural break given linear model
- Null hypothesis: no break
- Requires three OLS regressions
- Regression for entire period
- Two regressions, before and after break
- Collect sum-of-squared residuals
- Test statistic is distributed according to "F" distribution
The Chow test in Python
- Hypothesis: structural break in 1990 for China population
- Assume linear "factor model": $$\log(\text{Population}_t) = \alpha + \beta * \text{Year}_t + u_t$$
- OLS regression using
statsmodels'sOLSobject over full period 1950 - 2019- Retrieve sum-of-squared residual
res.ssr
- Retrieve sum-of-squared residual
import statsmodels.api as sm res = sm.OLS(log_pop, year).fit()print('SSR 1950-2019: ', res.ssr)
SSR 1950-2019: 0.29240576138055463
The Chow test in Python
- Break 1950 - 2019 into 1950 - 1989 and 1990 - 2019 sub-periods
- Perform OLS regressions on each sub-period
- Retrieve
res_before.ssrandres_after.ssr
- Retrieve
pop_before = log_pop.loc['1950':'1989']; year_before = year.loc['1950':'1989']; pop_after = log_pop.loc['1990':'2019']; year_after = year.loc['1990':'2019'];res_before = sm.OLS(pop_before, year_before).fit() res_after = sm.OLS(pop_after, year_after).fit()print('SSR 1950-1989: ', res_before.ssr) print('SSR 1990-2019: ', res_after.ssr)
SSR 1950-1989: 0.011741113017411783
SSR 1990-2019: 0.0013717593339608077
The Chow test in Python
- Compute the F-distributed Chow test statistic
- Compute the numerator
- k = 2 degrees of freedom = 2 OLS coefficients $\alpha$, $\beta$
- Compute the denominator
- 66 degrees of freedom = total number of data points (70) - 2*k
- Compute the numerator
numerator = (ssr_total - (ssr_before + ssr_after)) / 2denominator = (ssr_before + ssr_after) / 66chow_test = numerator / denominator print("Chow test statistic: ", chow_test, "; Critical value, 99.9%: ", 7.7)
Chow test statistic: 702.8715822890057; Critical value, 99.9%: 7.7
Let's practice!
Quantitative Risk Management in Python

