Risk exposure and loss

Quantitative Risk Management in Python

Jamsheed Shorish

Computational Economist

A vacation analogy

Hotel reservations for vacation
Pay in advance, before stay
- Low room rate
- Non-refundable: cancellation fee = 100% of room rate
Pay after arrival
- High room rate
- Partially refundable: cancellation fee of 20% of room rate

Image of boat near a Caribbean beach

Deciding between options

What determines your decision?
1. Chance of negative shock: illness, travel disruption, weather
  - Probability of loss
2. Loss associated with shock: amount or conditional amount
  - e.g. VaR, CVaR
3. Desire to avoid shock: personal feeling
  - Risk tolerance

Cartoon image of three children sick in bed with thermometers in mouths

Image of risk scale and money for risk management

Risk exposure and VaR

Risk exposure: probability of loss x loss measure
- Loss measure: e.g. VaR
10% chance of canceling vacation: P(Illness) = 0.10
Non-refundable:
- Total non-refundable hotel cost: € 500
- VaR at 90% confidence level: € 500
Partially refundable:
- Refundable hotel cost: € 550
- VaR at 90% confidence level: 20% cancellation fee x € 550 = € 110

Calculating risk exposure

Non-refundable exposure ("$\text{nr}$"):
- P(illness) x $\text{VaR}_{0.90}^{\text{nr}}$ = 0.10 x € 500 = € 50.
Partially refundable exposure ("$\text{pr}$"):
- P(illness) x $\text{VaR}_{0.90}^{\text{pr}}$ = 0.10 x € 110 = € 11.
Difference in risk exposure: € 50 - € 11 = € 39.
Total price difference between offers: € 550 - € 500 = € 50.
Risk tolerance: is paying € 50 more worth avoiding € 39 of additional exposure?

Risk tolerance and risk appetite

Risk-neutral: only expected values matter
- € 39 < € 50 $\Rightarrow$ prefer non-refundable option
Risk-averse: uncertainty itself carries a cost
- € 39 < € 50 $\Rightarrow$ prefer partially refundable option
Enterprise/institutional risk management: preferences as risk appetite
Individual investors: preferences as risk tolerance

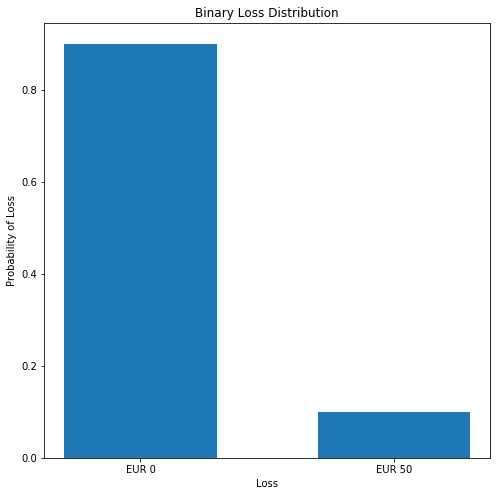
Loss distribution - discrete

Risk exposure depends upon loss distribution (probability of loss)
Vacation example: 2 outcomes from random risk factor

Bar chart of binary losses from vacation example

Loss distribution - continuous

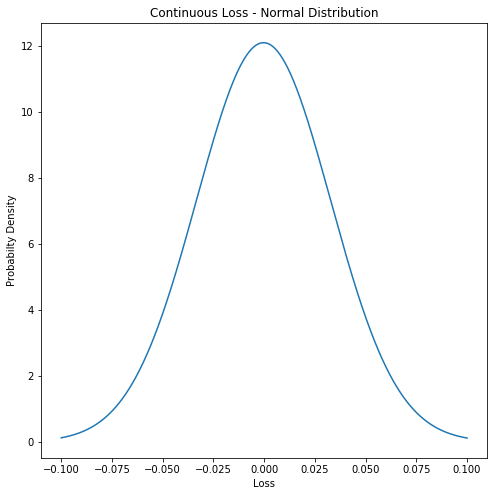
Risk exposure depends upon loss distribution (probability of loss)
Vacation example: 2 outcomes from random risk factor
More generally: continuous loss distribution
- Normal distribution: good for large samples

Image of continuous normal distribution

Loss distribution - continuous

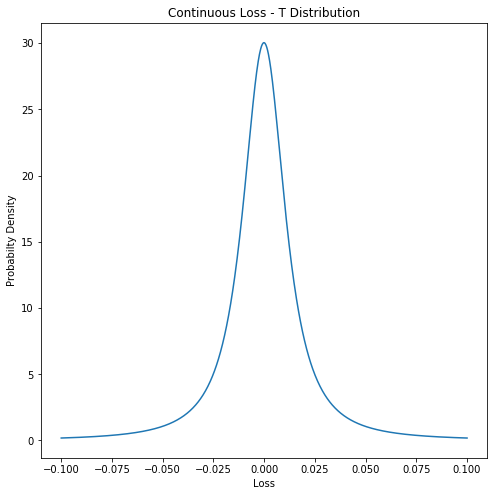
Risk exposure depends upon loss distribution (probability of loss)
Vacation example: 2 outcomes from random risk factor
More generally: continuous loss distribution
- Normal distribution: good for large samples
- Student's t-distribution: good for smaller samples

Image of continuous loss T distribution

Primer: Student's t-distribution

Also referred to as T distribution
Has "fatter" tails than Normal for small samples
- Similar to portfolio returns/losses
As sample size grows, T converges to Normal distribution

Image of continuous loss distribution

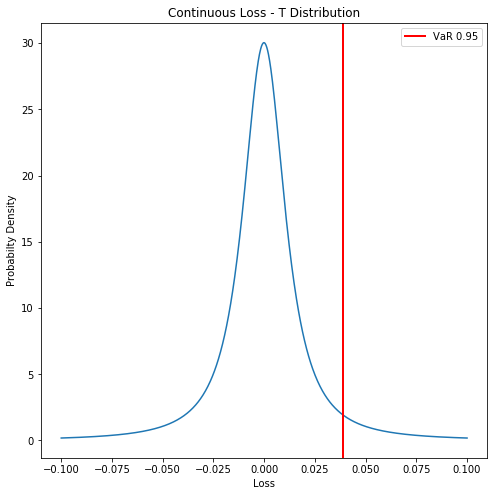
T distribution in Python

Example: compute 95% VaR from T distribution
- Import t distribution from scipy.stats
- Fit portfolio_loss data using t.fit()

from scipy.stats import t

params = t.fit(portfolio_losses)

Image of continuous loss distribution

T distribution in Python

Example: compute 95% VaR from T distribution
- Import t distribution from scipy.stats
- Fit portfolio_loss data using t.fit()
- Compute percent point function with .ppf() to find VaR

from scipy.stats import t

params = t.fit(portfolio_losses)

VaR_95 = t.ppf(0.95, *params)

Image of continuous loss T distribution with VaR

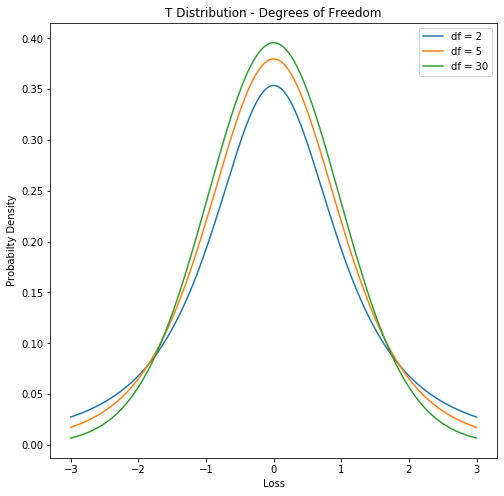
Degrees of freedom

Degrees of freedom (df): number of independent observations
Small df: "fat tailed" T distribution
Large df: Normal distribution

x = np.linspace(-3, 3, 100)

plt.plot(x, t.pdf(x, df = 2))

plt.plot(x, t.pdf(x, df = 5))

plt.plot(x, t.pdf(x, df = 30))

Image of T distribution for 30 degrees of freedom

Let's practice!

Quantitative Risk Management in Python

Preparing Video For Download...