Linear regression model

Practicing Statistics Interview Questions in R

Zuzanna Chmielewska

Actuary

Linear regression model

Linear regression model

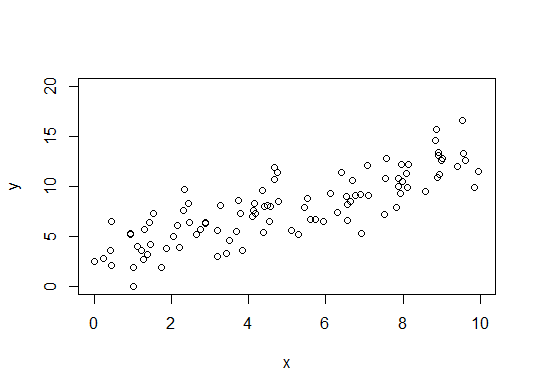
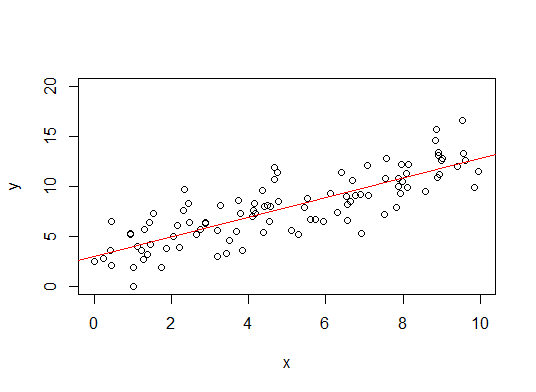
Linear regression model

$$ y_i = \beta_0 + \beta_1 \cdot x_{i1} + ... + \beta_p \cdot x_{ip} + e_{i}$$ where:

• $y_i$ - dependent variable,
• $x_{ij}$ - independent variables,
• $\beta_{j}$ - parameters,
• $e_i$ - error.

Linear predictor function

$$ \hat{y_i} = \beta_0 + \beta_1 \cdot x_{i1} + ... + \beta_p \cdot x_{ip}$$

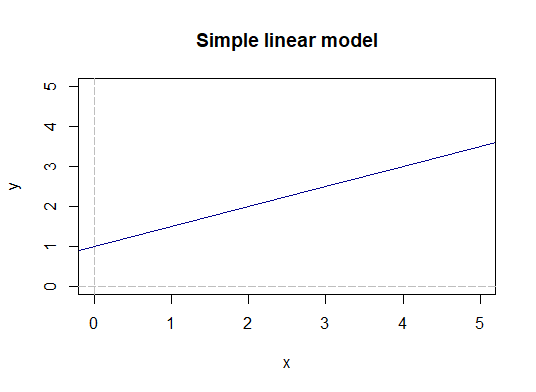$$ \hat{y_i} = \beta_0 + \beta_1 \cdot x_{i} $$

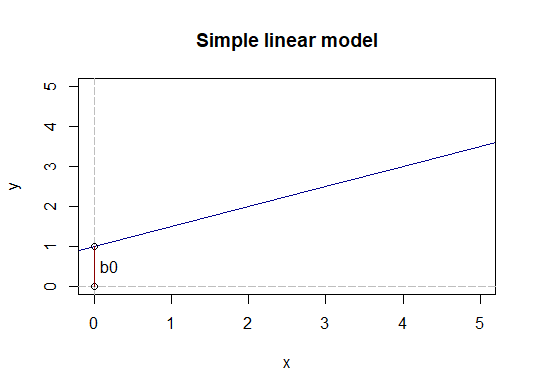$$ \hat{y_i} = \beta_0 + \beta_1 \cdot x_{i} $$

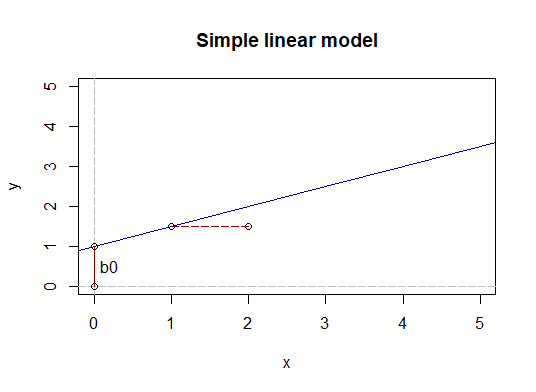$$ \hat{y_i} = \beta_0 + \beta_1 \cdot x_{i} $$

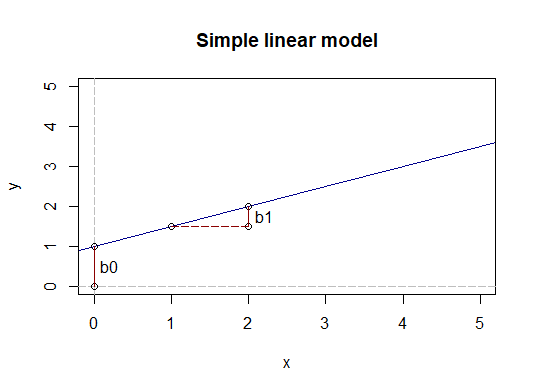$$ \hat{y_i} = \beta_0 + \beta_1 \cdot x_{i} $$

Log-transformation

Examples: $$ \hat{y_i} = \beta_0 + \beta_1 \cdot ln(x_{i1}) + ... + \beta_p \cdot x_{ip}$$

$$ ln(\hat{y_i}) = \beta_0 + \beta_1 \cdot x_{i1} + ... + \beta_p \cdot x_{ip}$$

Assumptions

• Linear relationship
• Normally distributed errors
• Homoscedastic errors
• Independent observations

Linear model in R

model <- lm(dist ~ speed, data = cars)

print(model)

Call:
lm(formula = dist ~ speed, data = cars)

Coefficients:
(Intercept)        speed  
    -17.579        3.932

Linear model in R

model <- lm(dist ~ speed, data = cars)
new_car <- data.frame(speed = 17.5)

predict(model, newdata = new_car)

       1 
51.23806

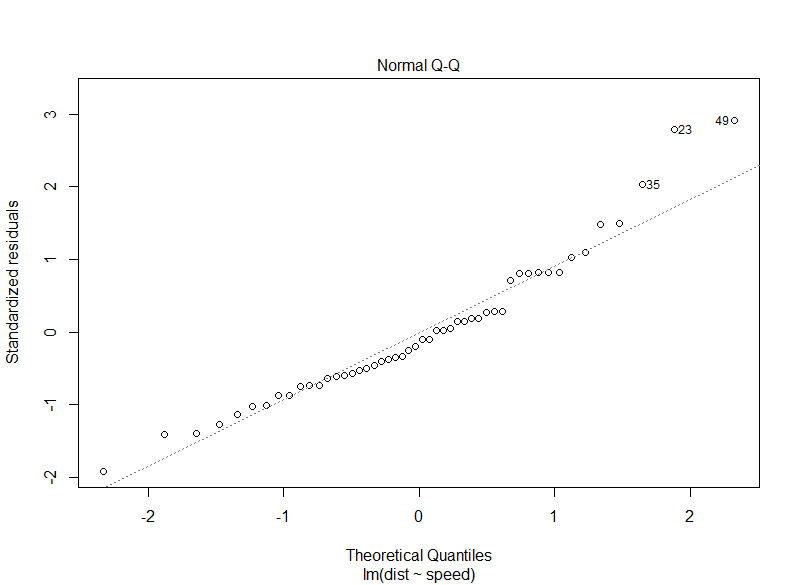
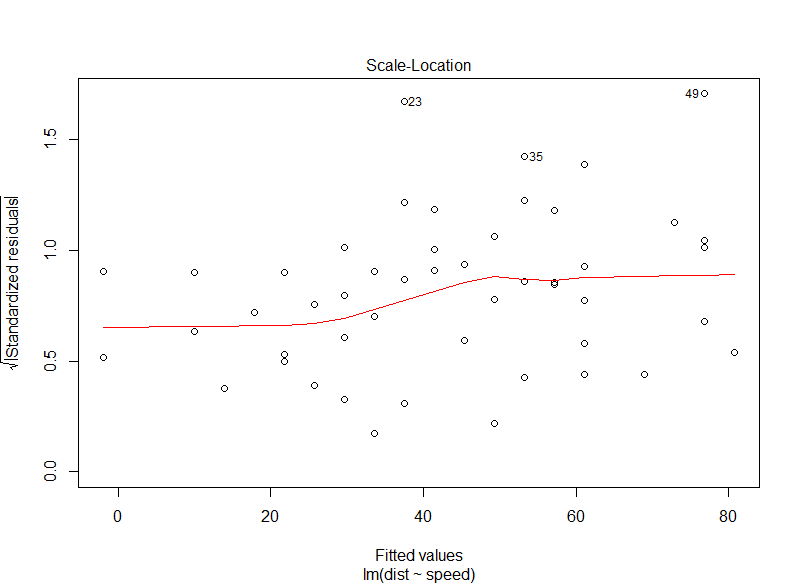
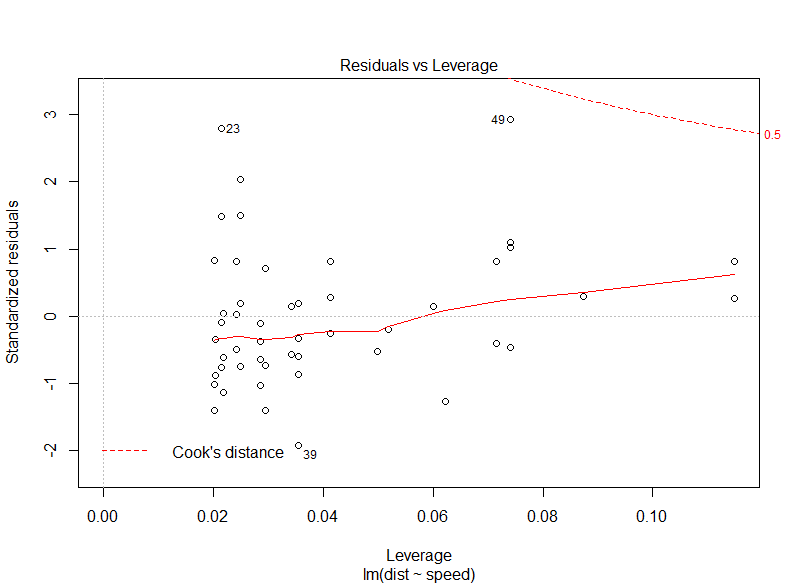
Diagnostic plots

model <- lm(dist ~ speed, data = cars)
plot(model)

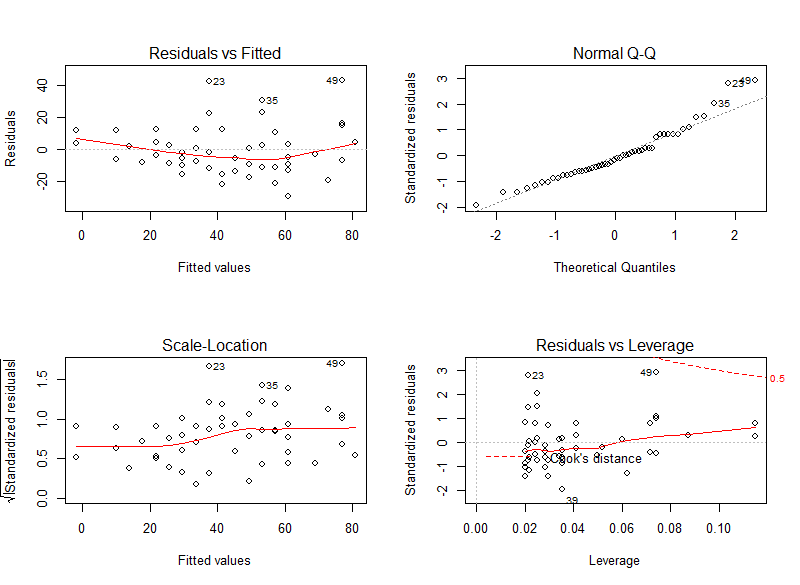
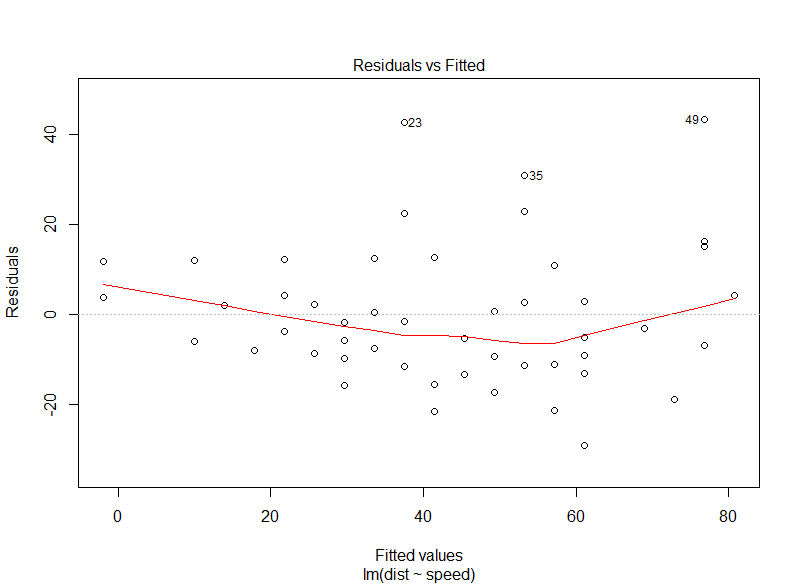
Summary

• linear regression model
• linear predictor function
• lm() in R
• diagnostic plots

Let's practice!

Practicing Statistics Interview Questions in R