Discrete distributions

Practicing Statistics Interview Questions in R

Zuzanna Chmielewska

Actuary

Probability

Overview of common distributions

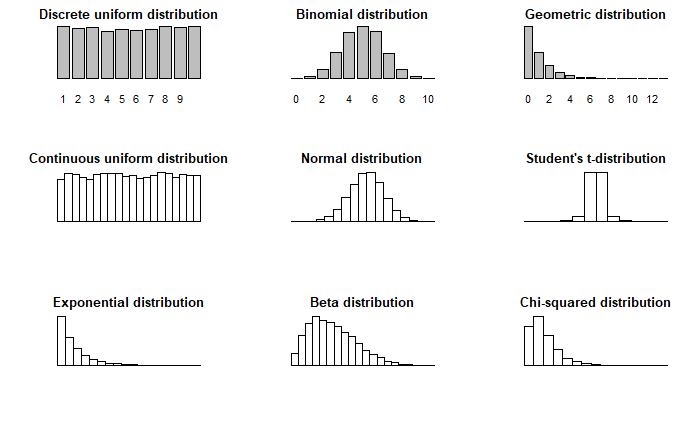
Probability functions in R

prefix	purpose	example
d	density	dnorm()

Probability functions in R

prefix	purpose	example
d	density	dnorm()
p	distribution function	pnorm()

Probability functions in R

prefix	purpose	example
d	density	dnorm()
p	distribution function	pnorm()
q	quantile function	qnorm()

Probability functions in R

prefix	purpose	example
d	density	dnorm()
p	distribution function	pnorm()
q	quantile function	qnorm()
r	random variates	rnorm()

Discrete uniform distribution

Discrete uniform distribution

Discrete uniform distribution

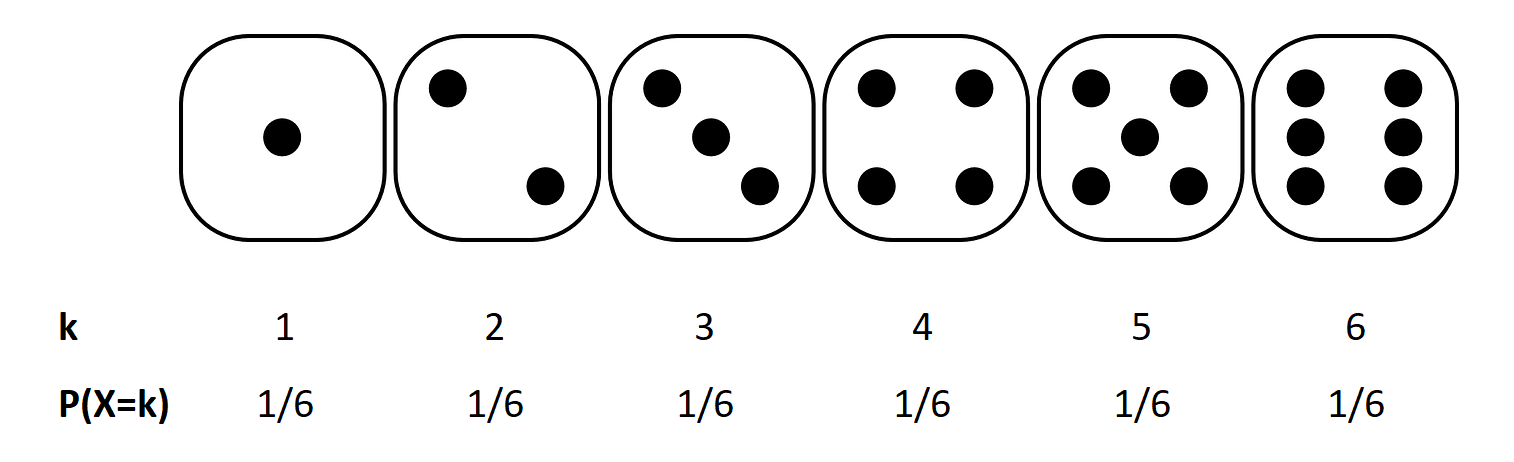
Discrete uniform distribution

sample(1:6, size = 1)

[1] 1

purrr::rdunif(n = 1, b = 6, a = 1)

[1] 2

Bernoulli distribution

Probability mass function: $$ P(X = 1) = p $$

$$ P(X = 0) = 1-p $$

Bernoulli distribution

$$ p = 0.5 $$

Binomial distribution

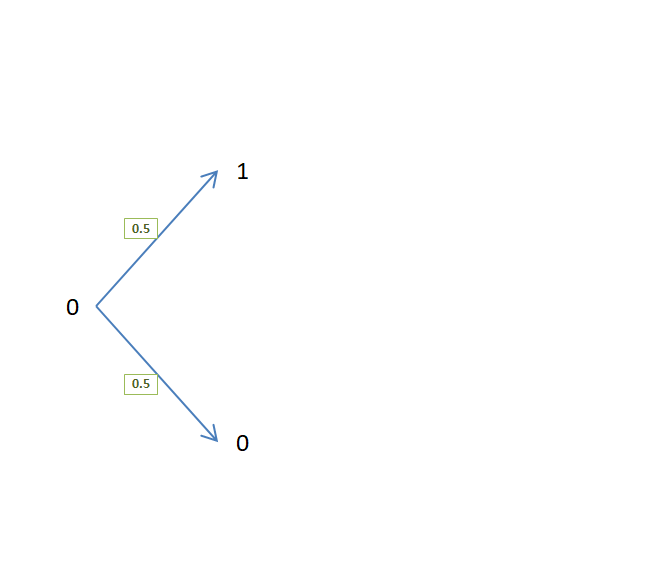
Binomial distribution

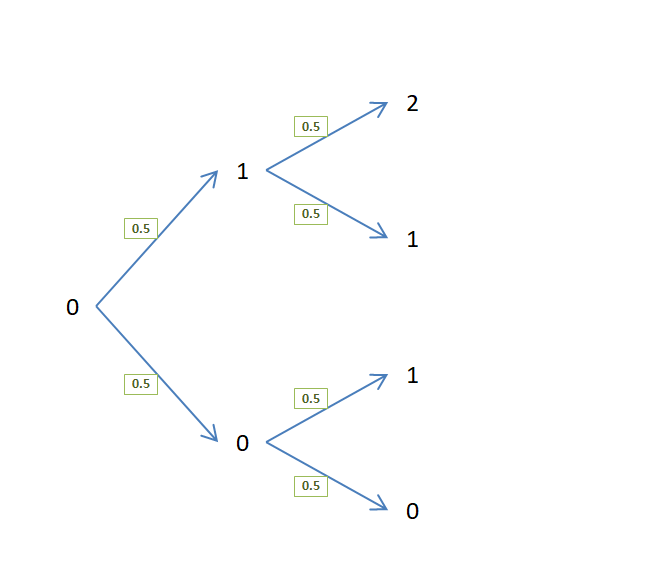
Binomial distribution

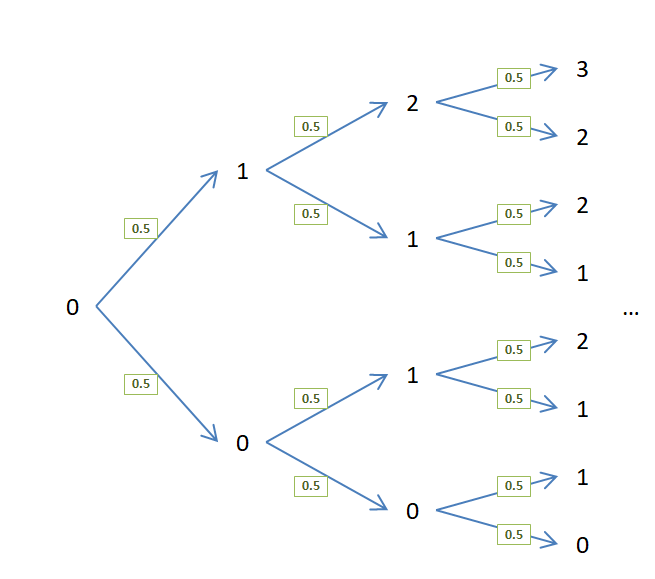
Binomial distribution

$$ P(X=k)=\binom{n}{k}p^k(1-p)^{n-k} $$

Binomial distribution

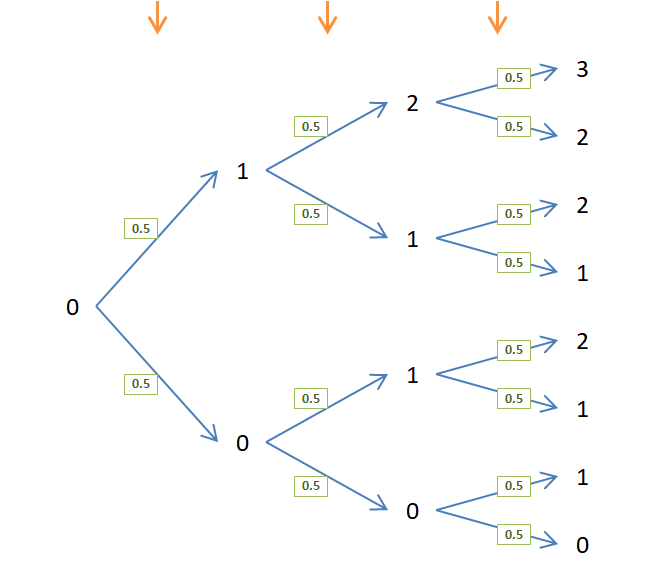
$$ P(X=k)=\binom{n}{k}p^k(1-p)^{n-k} $$

Binomial distribution

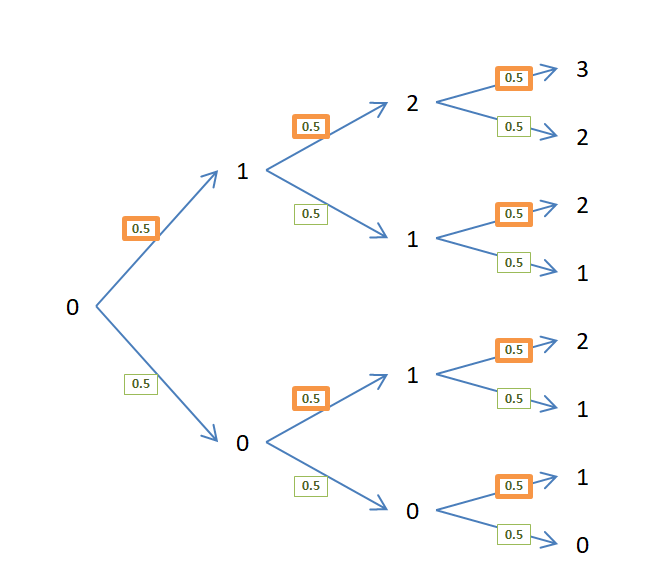
$$ P(X=k)=\binom{n}{k}p^k(1-p)^{n-k} $$

Binomial distribution

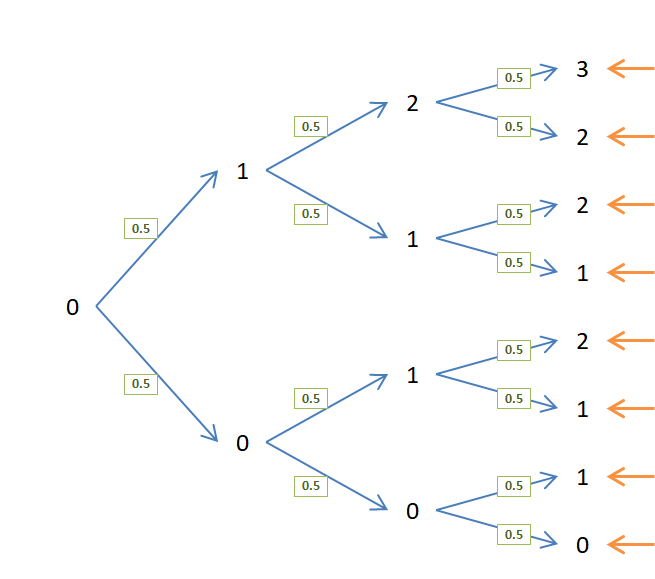
$$ P(X=k)=\binom{n}{k}p^k(1-p)^{n-k} $$

Binomial distribution in R

Binomial distribution:

rbinom(n, size = k, prob = p)

Bernoulli distribution:

rbinom(n, size = 1, prob = p)

Frequency table

random_numbers <- sample(1:10, size = 1000, replace = TRUE)

table(random_numbers)

random_numbers
  1   2   3   4   5   6   7   8   9  10 
101 106  82 102  91 104 105 106 109  94

Frequency chart

random_numbers <- sample(1:10, size = 1000, replace = TRUE)

barplot(table(random_numbers))

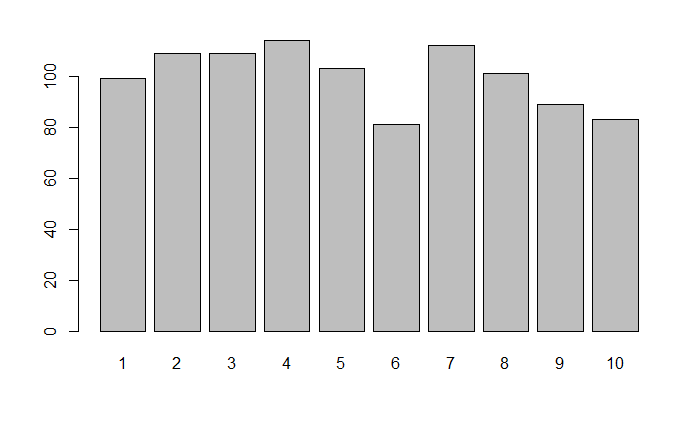
Reproducibility

set.seed(123)

sample(1:10, size = 3)
sample(1:10, size = 3)

3 10 2
2  6 3

Reproducibility

set.seed(123)
sample(1:10, size = 3)
set.seed(123)
sample(1:10, size = 3)

3 10 2
3 10 2

Summary

• probability functions in R
• common discrete distributions
  • discrete uniform
  • bernoulli
  • binomial
• frequency chart
• reproducibility

Let's practice!

Practicing Statistics Interview Questions in R