Covariance and correlation
Practicing Statistics Interview Questions in R

Zuzanna Chmielewska
Actuary
Covariance and correlation

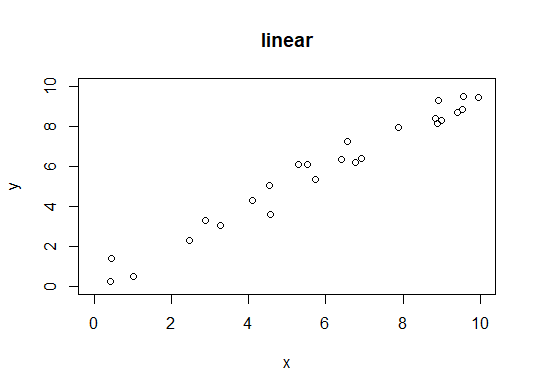
Covariance
Formula for a sample: $$ cov(X, Y) = \frac{\sum_{i = 1}^{n} (x_i - \overline{x}) \cdot (y_i - \overline{y})}{n-1} $$
Formula for a population: $$ cov(X, Y) = \frac{\sum_{i = 1}^{n} (x_i - \overline{x}) \cdot (y_i - \overline{y})}{n} $$
Covariance
Formula for a sample: $$ cov(X, Y) = \frac{\sum_{i = 1}^{n} (x_i - \overline{x}) \cdot (y_i - \overline{y})}{n-1} $$
Covariance
Formula for a population: $$ cov(X, Y) = \frac{\sum_{i = 1}^{n} (x_i - \overline{x}) \cdot (y_i - \overline{y})}{n} $$
Covariance - numerical example
$ x_1 = 3, x_2 = 5, x_3 = 7 $
$ y_1 = 6, y_2 = 11, y_3 = 13 $
$ \overline{x} = 5$
$ \overline{y} = 10$
$(x_1 - \overline{x}) \cdot (y_1 - \overline{y})= 8 $
$(x_2 - \overline{x}) \cdot (y_2 - \overline{y})= 0 $
$(x_3 - \overline{x}) \cdot (y_3 - \overline{y})= 6 $
$ \sum_{i=1}^{n} (x_i - \overline{x}) \cdot (y_i - \overline{y}) = 14$
$ \frac{\sum_{i=1}^{n} (x_i - \overline{x}) \cdot (y_i - \overline{y})}{n-1} = 7$
Correlation coefficient
$$ corr(X, Y) = \frac{cov(X, Y)}{\sigma_x \cdot \sigma_y} $$
Correlation coefficient
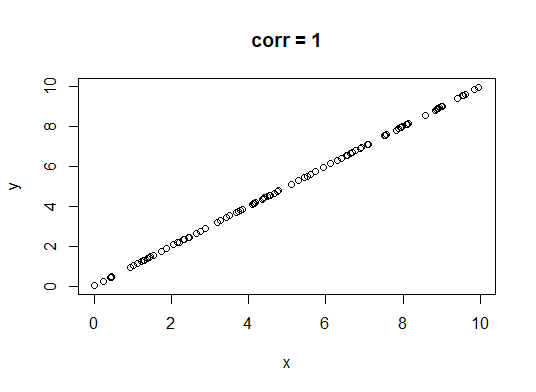
Correlation coefficient
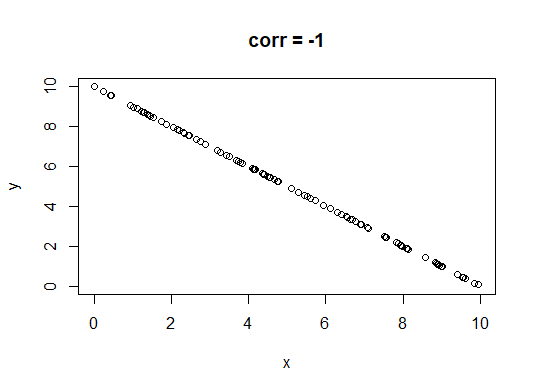
Correlation coefficient
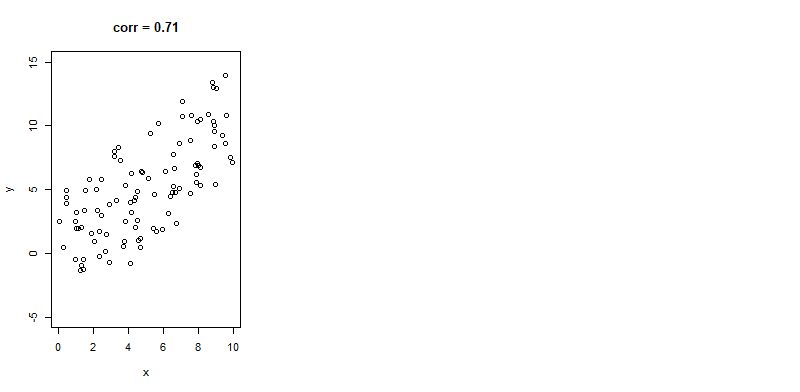
Correlation coefficient
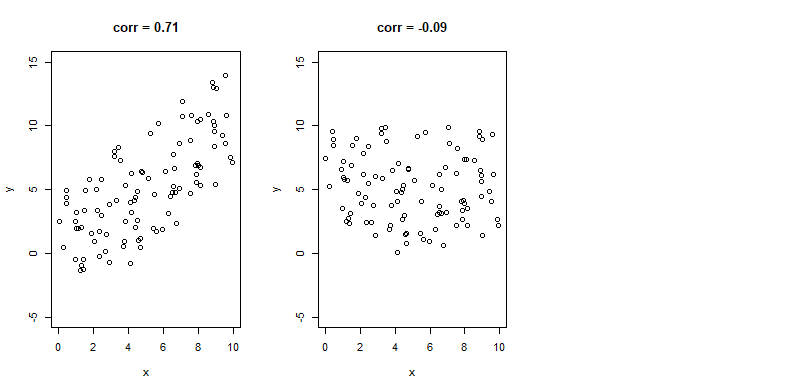
Correlation coefficient
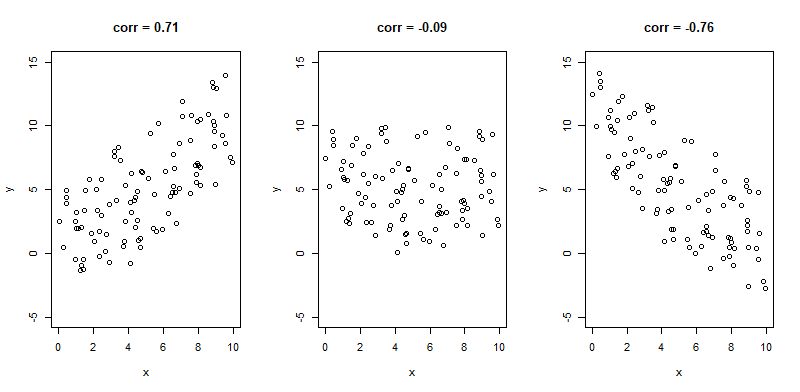
Correlation coefficient
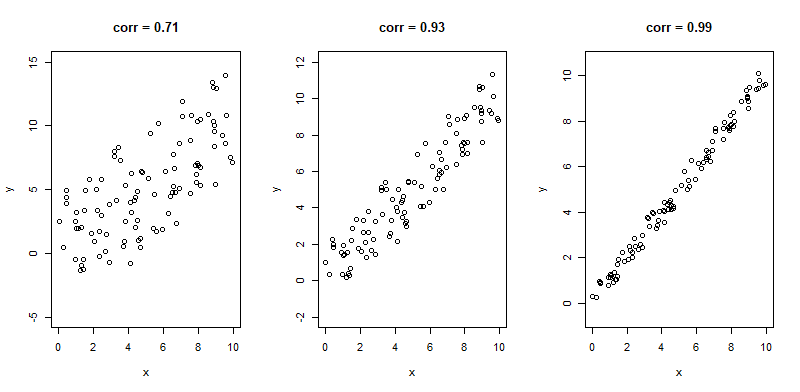
Nonlinear relationships
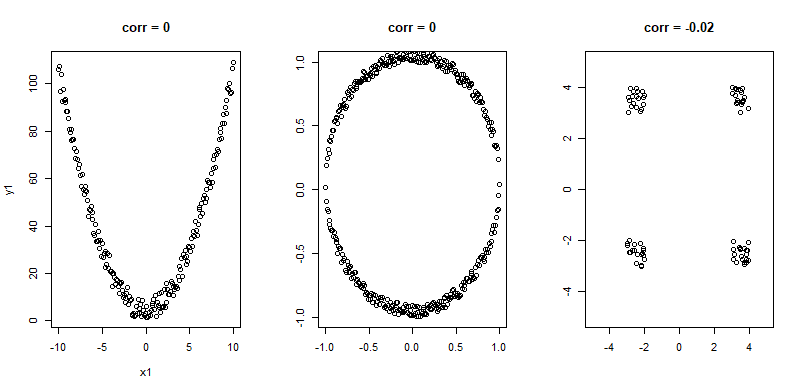
Correlation does not imply causation!

Summary
- covariance
- correlation coefficient
Let's practice!
Practicing Statistics Interview Questions in R

