What are ARCH and GARCH
GARCH Models in Python

Chelsea Yang
Data Science Instructor
First came the ARCH
Auto Regressive Conditional Heteroskedasticity
Developed by Robert F. Engle (Nobel prize laureate 2003)

Then came the GARCH
"Generalized" ARCH
Developed by Tim Bollerslev (Robert F. Engle's student)

Related statistical terms
White noise (z): Uncorrelated random variables with a zero mean and a finite variance
Residual = predicted value - observed value
Model notations
Expected return: $$ \mu_t = Expected[r_t | I(t-1)] $$
Residual (prediction error): $$ r_t = \mu_t + \epsilon_t $$
Expected volatility: $$\sigma^2 = Expected[(r_t - \mu_t)^2 | I(t-1)]$$
Volatility is related to the residuals: $$ \epsilon_t = \sigma_t * \zeta (WhiteNoise)$$
Model equations: ARCH
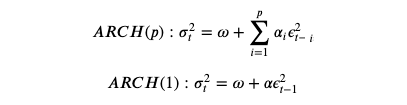
Model equations: GARCH
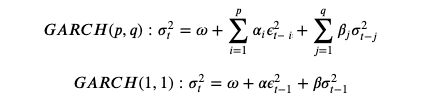
Model intuition
Autoregressive: predict future behavior based on past behavior
Volatility as a weighted average of past information

GARCH(1,1) parameter constraints
To make the GARCH(1,1) process realistic, it requires:
- All parameters are non-negative, so the variance cannot be negative.
$$\omega, \alpha, \beta >= 0 $$
- Model estimations are "mean-reverting" to the long-run variance.
$$\alpha + \beta <1$$
long-run variance: $$\omega / (1-\alpha - \beta)$$
GARCH(1,1) parameter dynamics
- The larger the $\alpha$, the bigger the immediate impact of the shock
- The larger the $\beta$, the longer the duration of the impact
Let's practice!
GARCH Models in Python

