Dynamic Beta in portfolio management

GARCH Models in Python

Chelsea Yang

Data Science Instructor

What is Beta

  • Stock Beta:

a measure of stock volatility in relation to the general market

  • Systematic risk:

the portion of the risk that cannot be diversified away

GARCH Models in Python

Beta in portfolio management

_Gauge investment risk _

Market Beta = 1: used as benchmark

Beta > 1: the stock bears more risks than the general market

Beta < 1: the stock bears less risks than the general market

GARCH Models in Python

Beta in CAPM

  • Estimate risk premium of a stock

CAPM: Capital Asset Pricing Model

$E(R_s)$ = $R_f$ + $\beta $($E(R_m)- R_f$)

  • $E(R_s)$: stock required rate of return
  • $R_f$: risk-free rate (e.g. Treasuries)
  • $E(R_m)$: market expected return (e.g. S&P 500)
  • $E(R_m)- R_f$: Market premium
GARCH Models in Python

Dynamic Beta with GARCH

$Beta$ = $\rho$ * $\sigma$_stock / $\sigma$__market

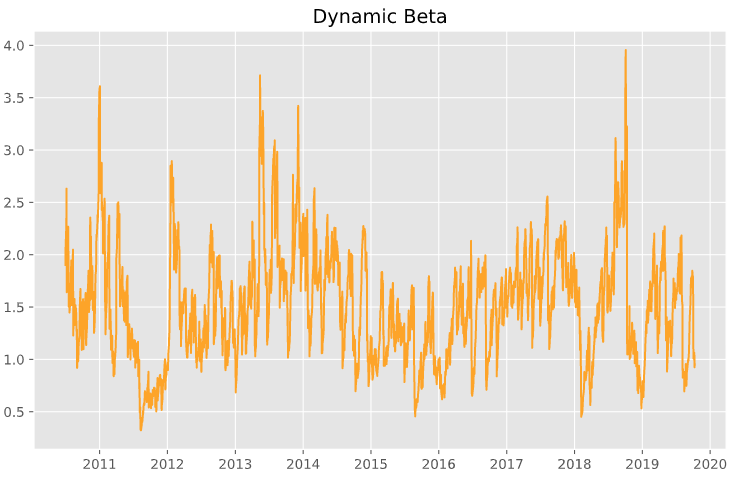
Plot of Beta

GARCH Models in Python

Calculate dynamic Beta in Python

1). Compute correlation between S&P500 and stock

resid_stock = stock_gm.resid / stock_gm.conditional_volatility
resid_sp500 = sp500_gm.resid / sp500_gm.conditional_volatility

correlation = numpy.corrcoef(resid_stock, resid_sp500)[0, 1]

2). Compute dynamic Beta for the stock

stock_beta = correlation * (stock_gm.conditional_volatility / 
                            sp500_gm.conditional_volatility)
GARCH Models in Python

Let's practice!

GARCH Models in Python

Preparing Video For Download...