Multiple imputation by bootstrapping

Handling Missing Data with Imputations in R

Michal Oleszak

Machine Learning Engineer

Uncertainty from imputation

  • Imputation is typically a first step before analysis or modeling.
  • Missing values are estimated with some uncertainty.
  • This uncertainty should be accounted for in any analyses carried out on imputed data.

The header of the title page of the paper by Ranjit Lall entitled "How Multiple Imputation Makes a Difference."

In almost half of the studies, key results disappear

Handling Missing Data with Imputations in R

Bootstrap

Bootstrapping = sampling rows with replacement to get original-size data

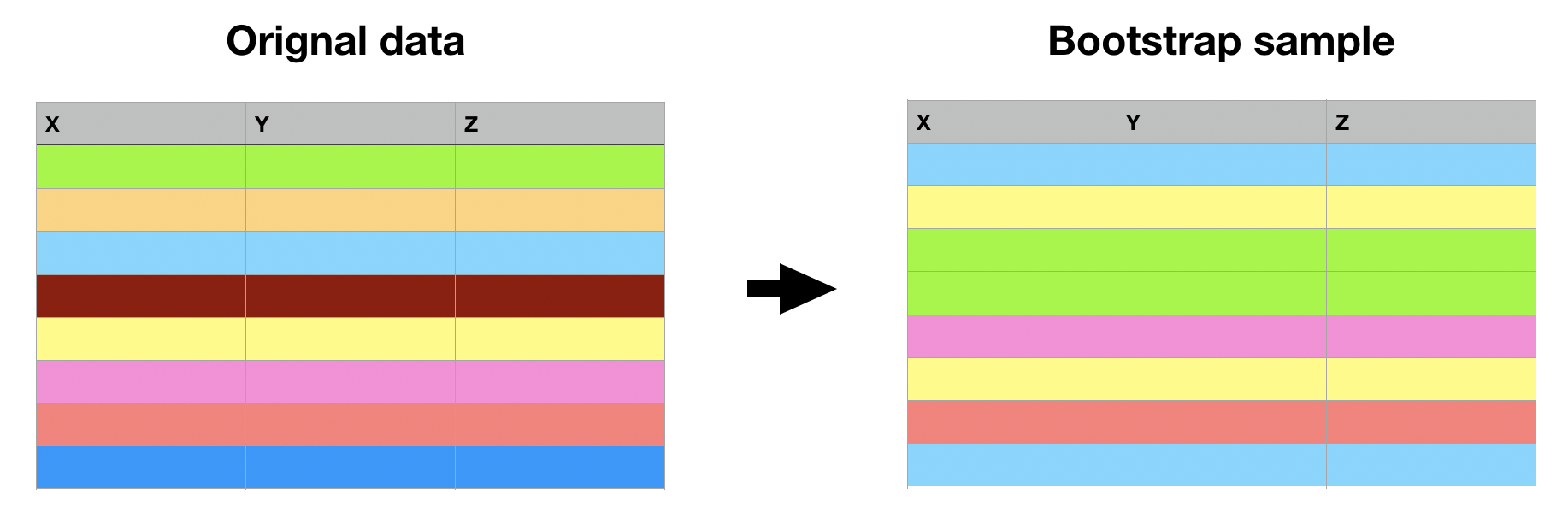
Two mock-up data frames. The left one, labeled "original data", has each row in different color, denoting the contain different values. In the right one, labeled "bootstrapped sample", some of the colored rows from the "original data" appear more than once, while others are not there at all.

Handling Missing Data with Imputations in R

Multiple imputation by bootstrapping

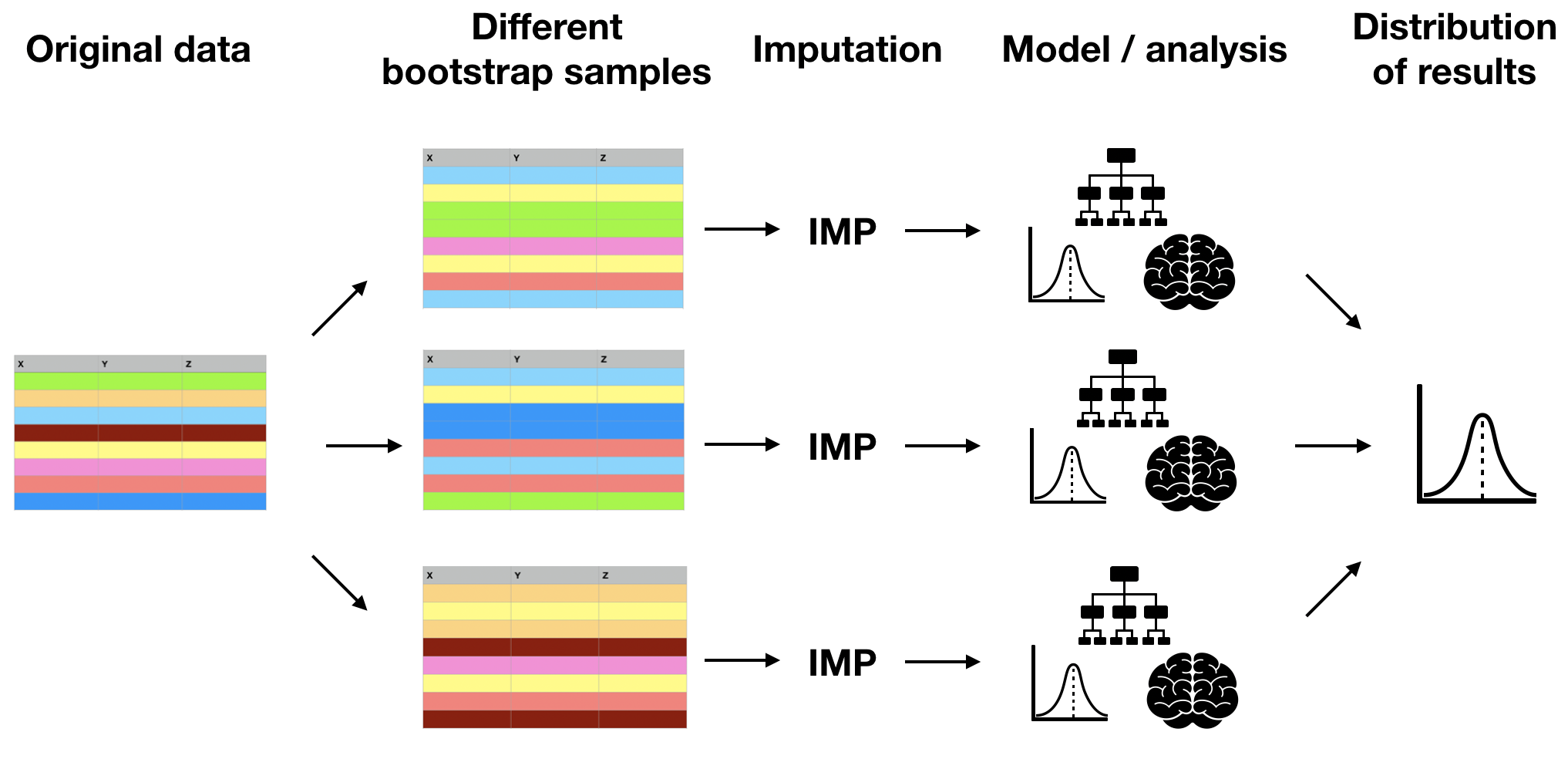
A diagram showing five stages of imputation by bootstrapping. From a mock-up data frame, called "original data", three arrows point to three other mock-up data frames labeled "different bootstrap samples". From each of them, an arrow points to an "Imputation" step. From there, arrows point to "Modeling / analysis" step. From there, arrows point to a single final node called "Distribution of results".

Handling Missing Data with Imputations in R

Bootstrapped imputation: pros & cons

Pros:

  • Works with any imputation method.
  • Can approximate quantities that are hard to compute analytically.
  • Work with MCAR and MAR data.

Cons:

  • Slow for many replicates or time-consuming computations.
Handling Missing Data with Imputations in R

Bootstrapping in practice

calc_correlation <- function(data, indices) {






  # Return the correlation coefficient
  return(corr_coeff)
}
Handling Missing Data with Imputations in R

Bootstrapping in practice

calc_correlation <- function(data, indices) {
  # Get bootstrap sample
  data_boot <- data[indices, ]




  # Return the correlation coefficient
  return(corr_coeff)
}
Handling Missing Data with Imputations in R

Bootstrapping in practice

calc_correlation <- function(data, indices) {
  # Get bootstrap sample
  data_boot <- data[indices, ]
  # Impute with kNN imputation
  data_imp <- kNN(data_boot)


  # Return the correlation coefficient
  return(corr_coeff)
}
Handling Missing Data with Imputations in R

Bootstrapping in practice

calc_correlation <- function(data, indices) {
  # Get bootstrap sample
  data_boot <- data[indices, ]
  # Impute with kNN imputation
  data_imp <- kNN(data_boot)
  # Calculate correlation between Weight and TotChol
  corr_coeff <- cor(data_imp$Weight, data_imp$TotChol)
  # Return the correlation coefficient
  return(corr_coeff)
}
Handling Missing Data with Imputations in R

Bootstrapping in practice

library(boot)
boot_results <- boot(nhanes, statistic = calc_correlation, R = 50)
print(boot_results)

ORDINARY NONPARAMETRIC BOOTSTRAP

Call:
boot(data = nhanes, statistic = calc_correlation, R = 50)

Bootstrap Statistics :
      original      bias    std. error
t1* 0.03028306 0.007385452  0.04207152
Handling Missing Data with Imputations in R

Plotting bootstrap results

plot(boot_results)

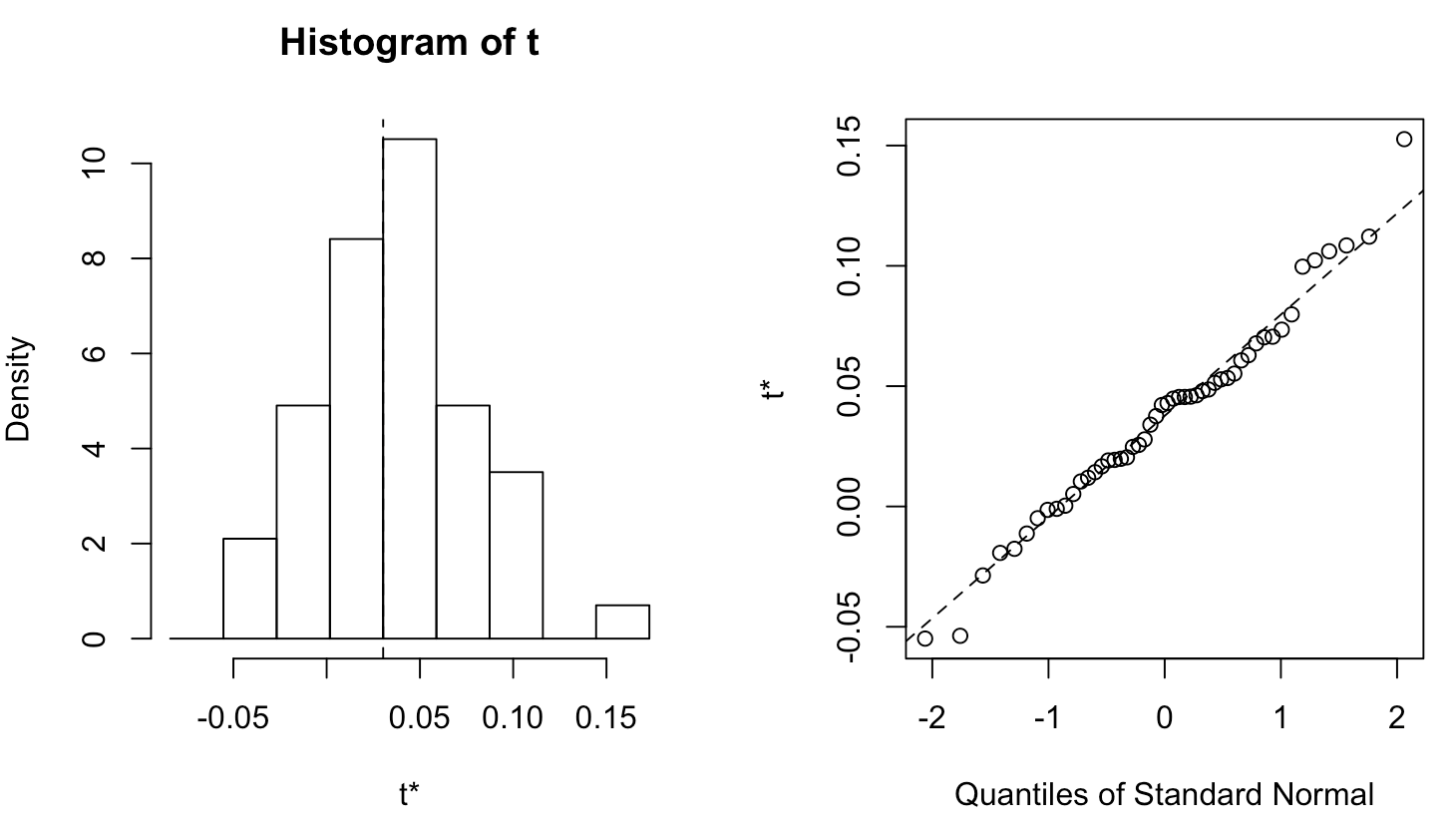
An histogram and a Q-Q plot showing the distribution of the bootstrapped results. Both plots suggest the distribution is closed to normal.

Handling Missing Data with Imputations in R

Bootstrapping confidence intervals

boot_ci <- boot.ci(boot_results, conf = 0.95, type = "norm")
print(boot_ci)

BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 50 bootstrap replicates

CALL : 
boot.ci(boot.out = boot_results, conf = 0.95, type = "norm")

Intervals : 
Level      Normal        
95%   (-0.0596,  0.1054 )  
Calculations and Intervals on Original Scale
Handling Missing Data with Imputations in R

Let's practice bootstrapping!

Handling Missing Data with Imputations in R

Preparing Video For Download...