A simple life insurance
Life Insurance Products Valuation in R

Roel Verbelen, Ph.D.
Statistician, Finity Consulting
The life insurance
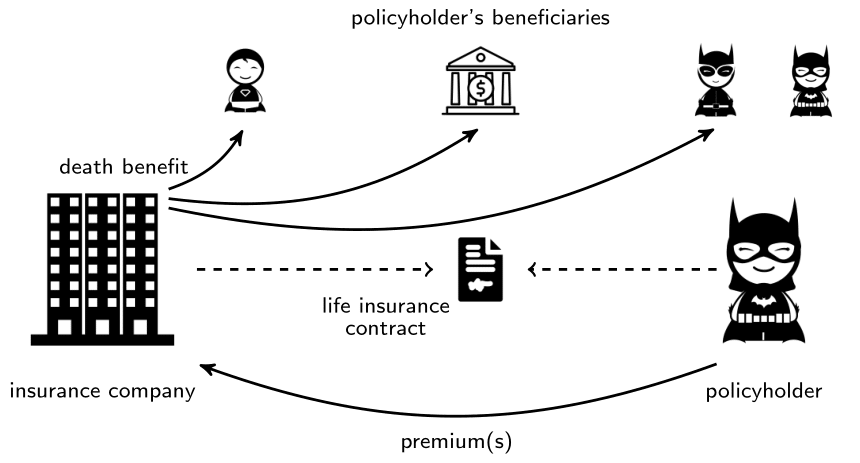
A simple life insurance
- The product is sold to $(x)$ at time 0.
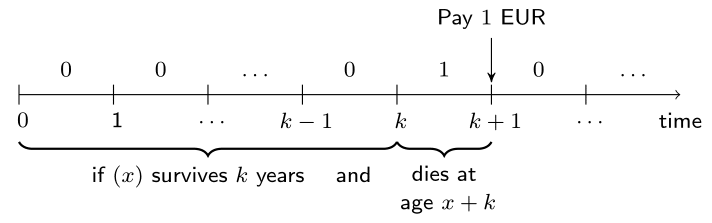
A simple life insurance
- Expected Present Value:
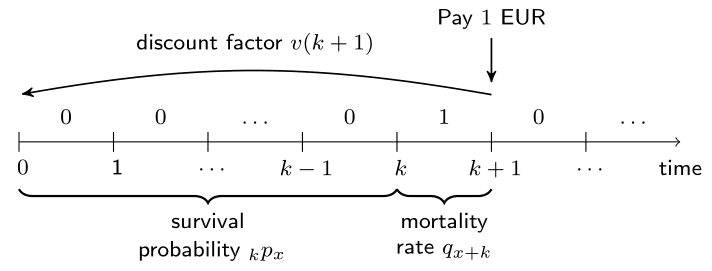
$\quad \,$ The EPV is
$$ {}_{k|1}A_{x} = 1 \cdot \ v(k+1) \cdot \ {}_kp_x \cdot \ q_{x+k} = 1 \cdot \ v(k+1) \cdot \ {}_{k|}q_{x} \, . $$
A simple life insurance in R
Compute ${}_{5|1}A_{65} = 1 \cdot \ v(6) \cdot \ {}_{5|}q_{65} = 1 \cdot \ v(6) \cdot \ {}_5p_{65} \cdot \ q_{70} $ for constant $i = 3\%$.
# Mortality rates and one-year survival probabilities
qx <- life_table$qx
px <- 1 - qx
# 5-year deferred mortality probability of (65)
kpx <- prod(px[(65 + 1):(69 + 1)])
kqx <- kpx * qx[70 + 1]
kqx
0.02086664
A simple life insurance in R (cont.)
# Discount factor
discount_factor <- (1 + 0.03) ^ - 6
discount_factor
0.8374843
# EPV of the simple life insurance
1 * discount_factor * kqx
0.01747548
Let's practice!
Life Insurance Products Valuation in R

