Dynamics

Life Insurance Products Valuation in R

Katrien Antonio, Ph.D.

Professor, KU Leuven and University of Amsterdam

Multiple dataframes with mortality rates

Look at $\{ q_x \} _{x\geq 0}$ or $\{p _ x \} _{x \geq 0}$ for multiple periods of time:

The evolution of mortality rates over time

$q_{x,t}$ is now the mortality rate for an $x$-year-old in period $t$.

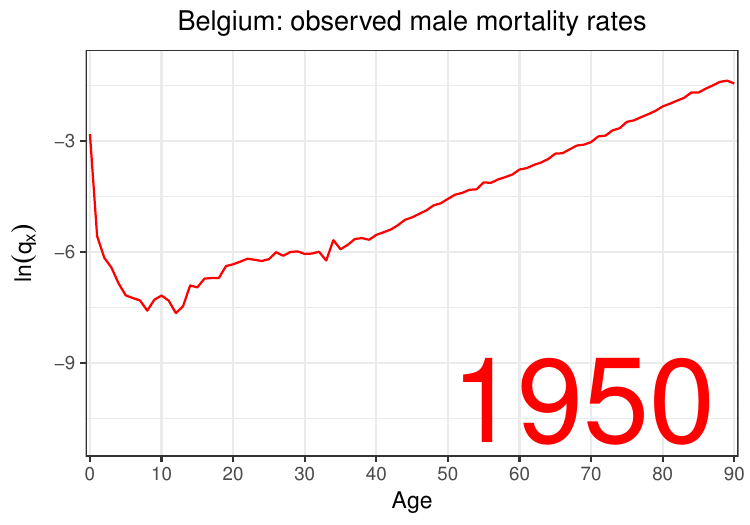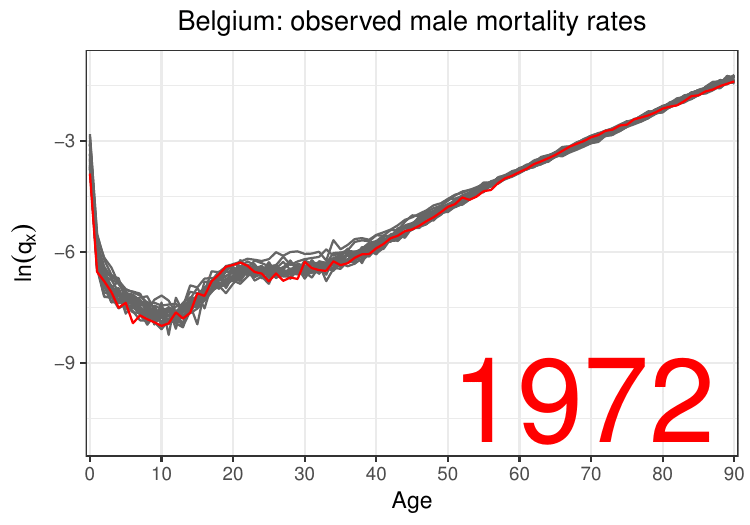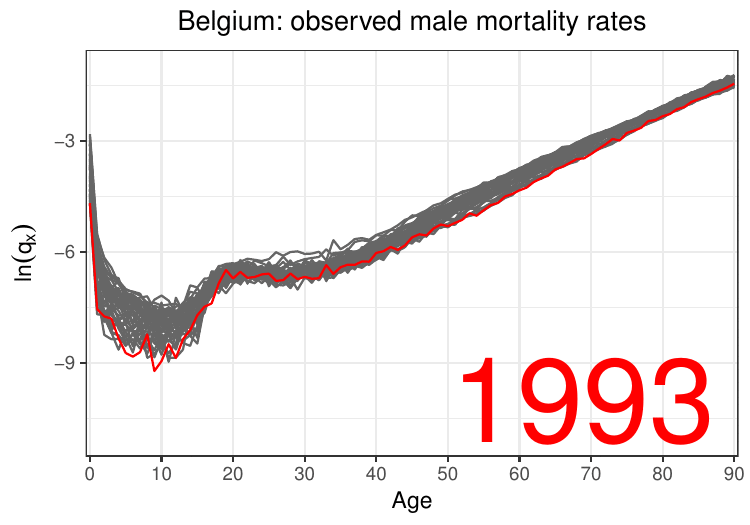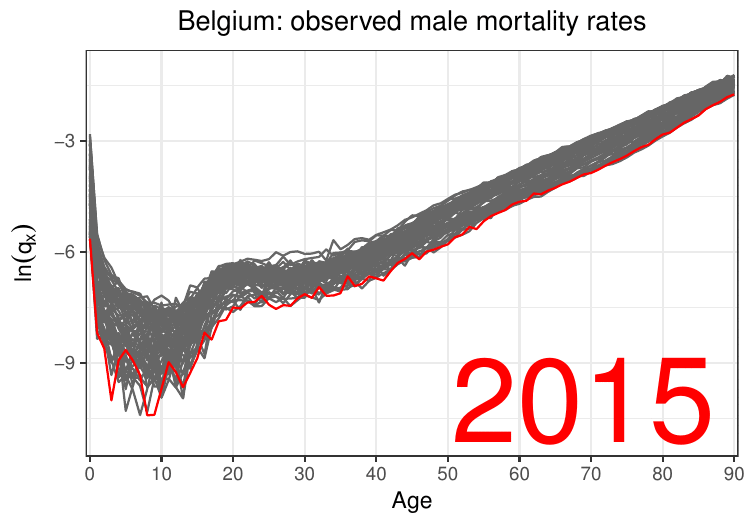
The period approach

Calculate survival probability $_kp_{x,t}$ in a vertical way:

$$ _kp_{x,t} = p_{x,t} \cdot p_{x+1,t} \cdot \ldots \cdot p_{x+k-1,t} $$

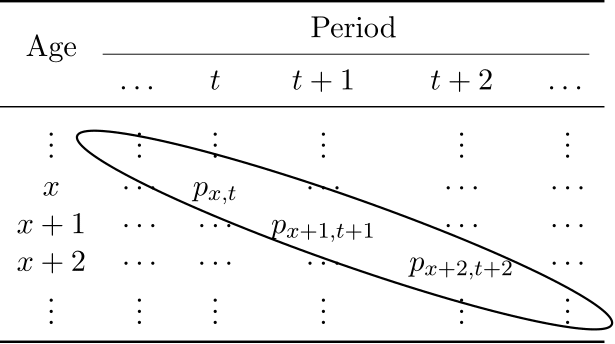
The cohort approach

Calculate survival probability $_kp_{x,t}$ in a diagonal way:

$$ _kp_{x,t} = p_{x,t} \cdot p_{x+1,t+1} \cdot \ldots \cdot p_{x+k-1,t+k-1} $$

Life tables over time in R

head(life_table)

  year age      qx     lx    dx    ex
1 1841   0 0.16580 100000 16580 40.28
2 1841   1 0.07148  83420  5963 47.22
3 1841   2 0.03905  77457  3025 49.82
4 1841   3 0.02306  74432  1716 50.82
5 1841   4 0.01693  72716  1231 51.01
6 1841   5 0.01233  71485   881 50.88

tail(life_table)

      year age      qx lx dx   ex
19420 2015 105 0.49719 40 20 1.46
19421 2015 106 0.51410 20 10 1.40
19422 2015 107 0.52979 10  5 1.35
19423 2015 108 0.54425  5  3 1.31
19424 2015 109 0.55749  2  1 1.28
19425 2015 110 1.00000  1  1 1.26

The period survival probabilities of a famous Belgian in R

Jacques Brel is a Belgian singer who was born in 1929 and died at age 49.
What is the probability $_{49|}q_{0, 1929}$ that a newborn, born in 1929, dies at age 49?
Period or vertical way:

period_life_table <- subset(life_table, year == 1929)
qx <- period_life_table$qx
px <- 1 - qx
prod(px[1:(48 + 1)]) * qx[49 + 1]

0.008456378

The cohort survival probabilities of a famous Belgian in R

Jacques Brel is a Belgian singer who was born in 1929 and died at age 49.
What is the probability $_{49|}q_{0, 1929}$ that a newborn, born in 1929, dies at age 49?
Cohort or diagonal way:

cohort_life_table <- subset(life_table, year - age == 1929)
qx <- cohort_life_table$qx
px <- 1 - qx
prod(px[(0 + 1):(48 + 1)]) * qx[49 + 1]

0.006410343

Let's practice!

Life Insurance Products Valuation in R