Change of period and term structure
Life Insurance Products Valuation in R

Roel Verbelen, Ph.D.
Statistician, Finity Consulting
Moving away from constant, yearly interest
Two questions:
How to deal with interest rates when applying a change of period (e.g. from years to months)?
How to go from constant interest rate to a rate that changes over time?
From yearly to $m$th-ly interest rates
Yearly interest rate $i$.
How to derive $i^{\star}_m$ the rate applicable to a period of $1/m$th year?
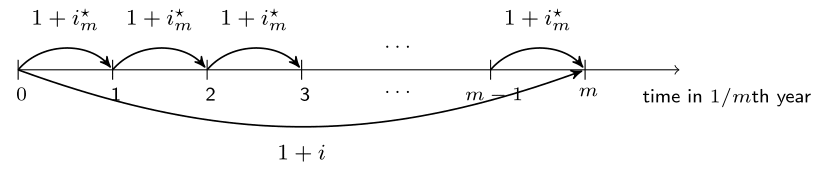
$\qquad$ Then:
$$ 1+i = (1+i^{\star}_m)^m \quad \Leftrightarrow \quad i^{\star}_m = (1+i)^{1/m}-1. $$
From yearly to $m$th-ly interest rates in R
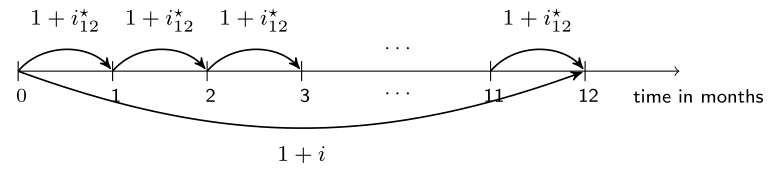
# Yearly interest rate i <- 0.03# Calculate the monthly interest rate (monthly_interest <- (1 + i) ^ (1 / 12) - 1)
0.00246627
# From monthly to yearly interest rate
(1 + monthly_interest) ^ 12 - 1
0.03
Non-constant interest rates
Observations:
interest rates are not necessarily constant;
the term structure of interest rates or yield curve.
Incorporate this in our notation and framework!
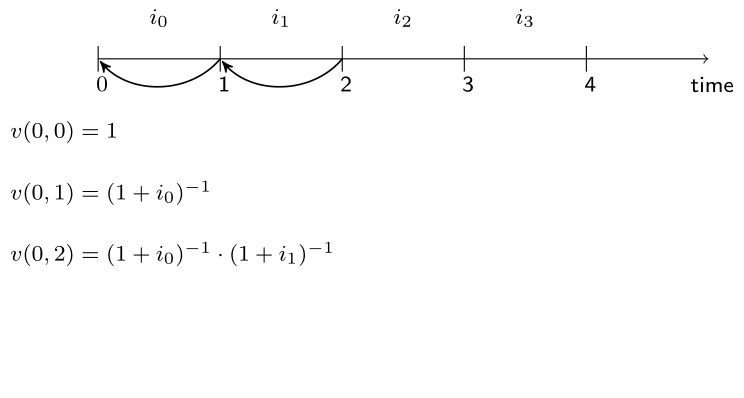
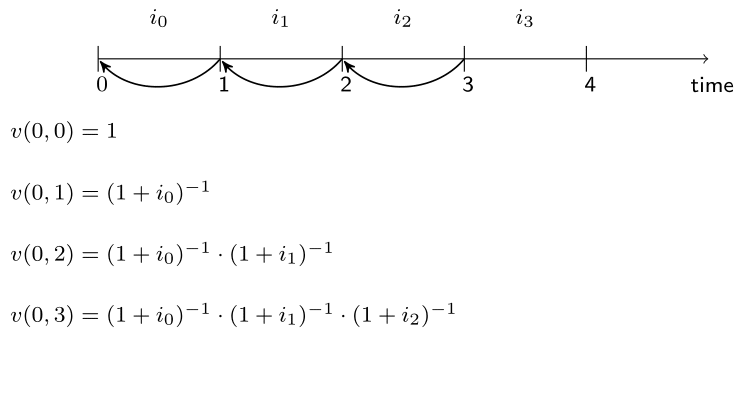
Non-constant interest rates
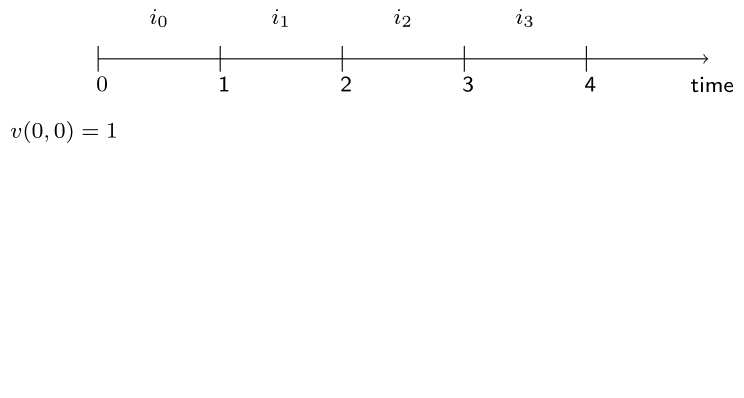
Non-constant interest rates
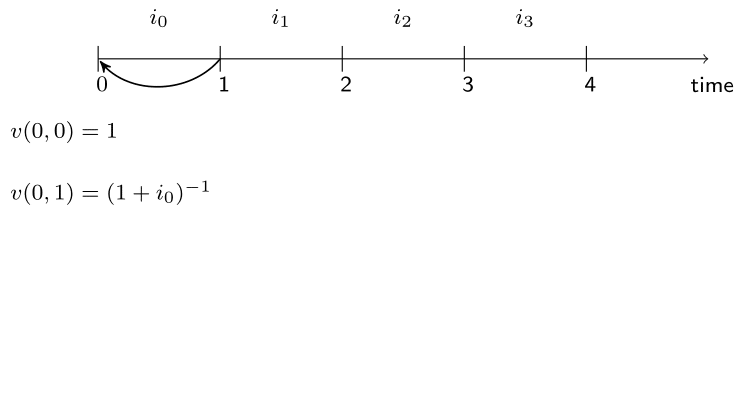
Non-constant interest rates
Non-constant interest rates
Non-constant interest rates
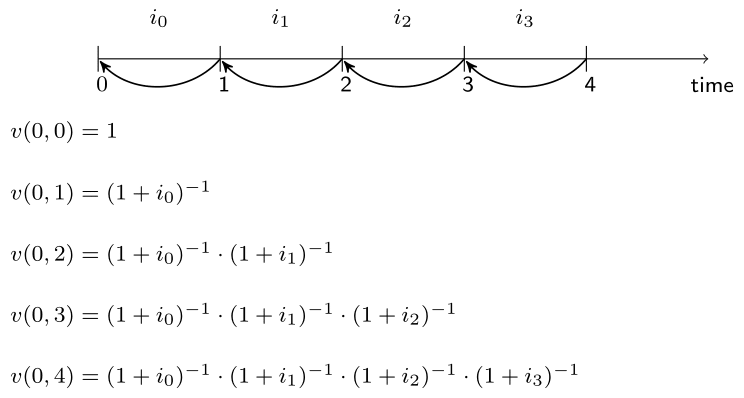

# Define the vector containing the interest rates
interest <- c(0.04, 0.03, 0.02, 0.01)
# Define the vector containing the inverse of 1 plus the interest rate
yearly_discount_factors <- (1 + interest) ^ - 1
# Define the discount factors to time 0 using cumprod()
discount_factors <- c(1 , cumprod(yearly_discount_factors))
discount_factors
1.0000000 0.9615385 0.9335325 0.9152279 0.9061663
Let's practice!
Life Insurance Products Valuation in R

